Lunar Recession
Does It Support a Young Universe?
We have had many people contact us concerning the recession rate of the moon. Hopefully this short article will help to clarify the details of lunar recession and why it supports a young universe.
[The July 11 AiG web] article mentioned the moon moving away from the earth at approximately 1.5 inches a year. It said that would be 250 meters in 6,000 years which I can get on my computer’s calculator program. It also mentioned the moon as being 400,000km away and that 1.5 billion years ago the earth and moon would be touching at that pace. However I get 9.6 billion years at the 1.5 inches a year pace and am not so sure that the moon moving away from the Earth would be constant. I would think that the speed at which the moon moves away from the Earth would be lower at lower distances due to planetary gravity? Is the author using logic somewhere to change the math that I am unaware of? At a closer distance from earth at a certain point the two would accelerate towards each other and collide I’m sure.. There has to be a minimum distance the moon would have to start away from Earth for this to not happen right? So how far is that distance and is that the factor I’m missing?
We have had many people contact us concerning the recession rate of the moon. Hopefully this short article will help to clarify the details of lunar recession and why it supports a young age for our solar system.
The recession of the moon is not constant over time. It would have been faster in the past. So, it is incorrect to assume that the rate has always been 4 cm/year.
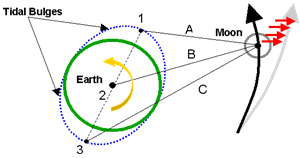
Figure 1. Past (theoretical) recession rate of the moon
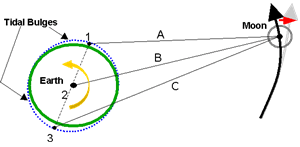
Figure 2. Present recession rate of the moon
Gravity is the force that keeps our moon in orbit around the earth. In Figures 1 and 2 this is represented by line “B.” If not for the gravity of the earth and moon, the moon would simply float away from the earth into space.
A major point to remember about lunar recession is that it is not constant over long periods of time. The further the moon moves away from the earth the more constant its recession seems to become.
In short, lunar recession is caused by tidal forces. Tidal forces are not the same thing as the gravity that keeps the moon orbiting around the earth. (However, they are caused by the moon’s gravity as will be shown.) The moon does more than just the rising and receding of tides along shorelines. When combined with the rotation of the earth and its gravity, these tidal forces are what cause the moon to recede away from the earth.
As we know, the moon causes tides; these are due to the fact that the moon’s gravitational force is stronger the closer you are to it. So, the moon’s gravity pulls more strongly on the side of Earth closest to the moon, and pulls less on the opposite side. This effectively “stretches” the Earth and produces two tidal bulges. The figure illustrates how the moon is actually pulling the oceans away from the earth toward itself (point 1) and causes the earth to bulge. At the same time there is a bulge produced on the opposite side of the earth (point 3) where the earth is being pulled away from the oceans.
Since the earth rotates faster than the moon orbits, the tidal bulge stays slightly ahead of the moon. With the earth bulging, the moon is “pulled” by the point of gravity (point 1), produced by the bulge, since it is closer to it (line A) than the point of gravity (point 3) at the opposite side of the earth (line C). Since the moon is constantly being pulled it is constantly accelerating. Even though the earth’s gravity (point 2) is acting as a centripetal force (line B) to keep the moon in an orbital path (dark arrow), the acceleration of the moon caused by the tidal bulge at point 1 is increasing its angular momentum, therefore moving it outward (gray arrow).
Ok, No offense to all the other awesome stuff you guys have on your website and all of the stuff you’re doing at the Creation Museum (something I check up on everyday for new pics by the way :) ), but this new “News to Note” is the best thing you’ve done yet. It helps put everything your ministry stands for in a cultural perspective—answering the critics immediately after they’ve published a news article spouting something “new” in regards to evolution.
AWESOME, AWESOME, AWESOME!
T.P.
USA
Figure 1 shows what the past (theoretical) recession rate would have looked like. Being much closer in a more-distant past, the moon would have caused larger tidal bulges, creating a greater “pulling” force (point 1, line A), increasing the angular momentum; thus the moon receded at a much greater speed (as shown by the red arrows).
With the earth where it is today (Figure 2) tidal bulges are much smaller (than the theoretical past), making the “pulling” force of point 1 smaller; thus the angular momentum is much less, resulting in the present and seemingly more-constant recession rate of 4 cm per year. The moon could never have been closer than 18,400 km (11,500 miles), known as the Roche Limit, because Earth’s tidal forces (i.e., the result of different gravitational forces on different parts of the moon) would have shattered it. This is explained in more detail In Dr. Jason Lisle book Taking Back Astronomy.
The equations (also taken from Dr. Lisle’s book) involved in the recession rate of the moon are thus:
k = r6dr/dt = (384,401 km)6 x (0.000038 km/year) = 1.2 x 1029 km7/year
∫0T dt = ∫0R (r6/k)dr
T = R7/(7k)
In His name and for His glory,
David Wright, AiG–USA
Recommended Resources

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- © 2024 Answers in Genesis








