Secrets to the Origin of Species: Demystifying “Genetic Drift”

Background

For years, genetic drift has been overshadowed by a much more familiar concept: natural selection, or the survival of the fittest to reproduce. It’s easy to see why. After all, Darwin put the term in the title of his book: On the origin of species by means of natural selection. To this day, to explain the design we see in nature, evolutionists rely heavily on natural selection—and not genetic drift:

While natural selection results in adaptation, genetic drift does not—so it is not responsible for those anatomical, physiological, and behavioral features of organisms that equip them for reproduction and survival.1

Combined with the simplicity of the concept—that the superior survive, and that the inferior die out—natural selection has dominated the discussion of the origin of species for 150 years.

Genetic drift has remained obscure and unknown to the vast majority of people.

In contrast, genetic drift has remained obscure and unknown to the vast majority of people. In short, genetic drift is the application of statistics to genetics. But never fear: the math is fairly easy to follow—and has remarkable relevance to the origin of species. We’ll soon discover that genetic drift was probably one of the major means by which species arose from the animal “kinds” on board the Ark with Noah.2

New Species and the Flood

When we’re dealing with genetic drift, the first helpful fact to recognize is that we’re not dealing with scientific laws. Instead, we’re dealing with probabilities. For example, consider a set of prospective parents. What scientific law can predict for them whether they will have a boy or a girl? Despite living in an advanced scientific age, we have no such law at our disposal—which is why gender-reveal parties are still a big hit among families! In the absence of this law, we resort to probabilities. On average, about 50% of children born are boys; 50% are girls. Deviations from this average occur—which is why these are probabilities, not laws. In statistical terms, most parents have a 50% chance of having a boy, and a 50% chance of having a girl. Conversely, we’re going to explore the formation of new species with probabilities.

As a helpful illustration, let’s consider the origin of the seven living equid species (e.g., horses, asses/donkeys, and zebras; see Figure 1). Based on breeding studies, they likely belong to the same biblical kind and have, therefore, descended from a single pair of equids on board the Ark. After the Flood, this pair exited the Ark and, over the last 4,500 years, gave rise to the seven living species we see today. Let’s take a more in-depth look at how genetic drift may have played a role in this process.

Figure 1. Compilation of images of the Equid kind from Wikimedia Commons.3

How could this single pair give rise to the striped and unstriped equids that roam that earth today?

As a starting point, let’s say that Noah brought on board the Ark a heterozygous pair of equids—a pair that had a mix of genetic information. (As a help, remember that the prefix homo- means the same; hetero- means different.) In sexually reproducing creatures, offspring inherit this genetic makeup from both parents. A zebra baby acquires half its DNA from its mother, half from its father. Furthermore, it’s not the case that the genetic information for the right side of the body comes from dad and the information for the left side from mom. Rather, both parents pass on information for the whole body. Then, the baby’s body utilizes the combination of information to produce its unique look—due to the heterozygous genetic information that it possesses as a result of having two parents.

To clarify, we’re not saying that the DNA in the male equid was completely different from the DNA in the female equid. Current data indicate that the vast majority of the DNA sequence was identical between the two individuals.4 However, at 25 million or more of their DNA sites (counter-intuitively, this is still a small fraction of their total DNA!), these two individuals had DNA differences.

How could this single pair give rise to the striped and unstriped equids that roam that earth today?

Genetic Drift and the Flood

To keep the discussion easy to follow, let’s oversimply the genetics. Let’s use A to designate the genetic information for stripes, and let’s use a to designate the genetic information for solids. (In our little example, out of the 25 million possible DNA sites where differences exist, we’re assuming that just one site is relevant to coat color—which is also an oversimplification.) A heterozygous pair on the Ark would have had a genetic makeup of Aa—the male would have been Aa, and the female also would have been Aa. These parents may have been semi-striped, similar to the horse-zebra and donkey-zebra hybrids that we have in our petting zoo at the Creation Museum (Figure 2).

Figure 2. The zorse and zonkey at the Creation Museum petting zoo interacting with one another.

With a Punnett Square, we can predict the probabilities that these parents would produce striped or unstriped offspring:

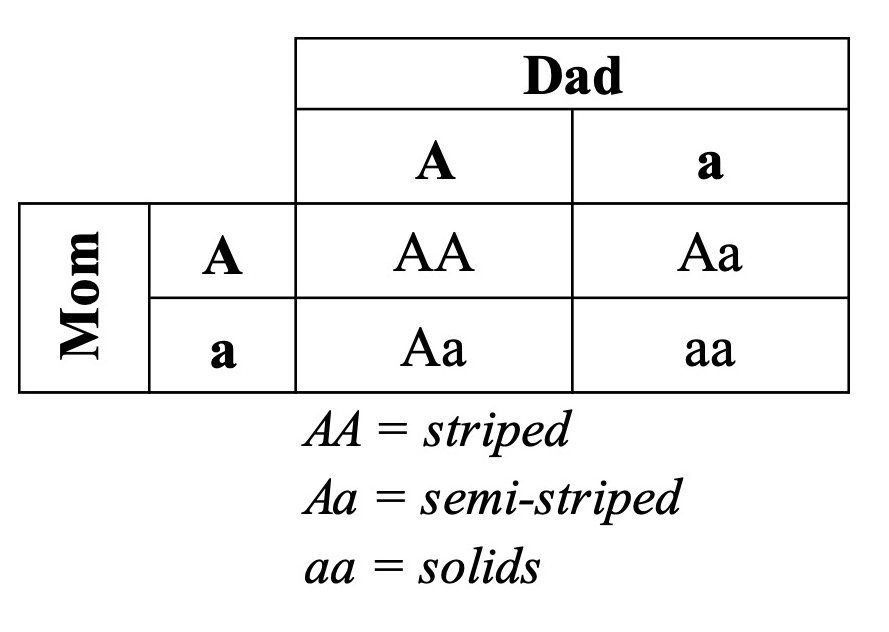
Thus, on average, about 25% (1 in 4) of the offspring will be striped (i.e., AA), 25% (1 in 4) will be a solid color (i.e., aa), and 50% (2 in 4) will be semi-striped like the parents (i.e., Aa). Or, in probability terms, their offspring have a 25% chance of being striped, a 25% chance of being solid-colored, and a 50% chance of remaining the same as the parents.

The process of speciation in the wild is not like the process of breeding on farms and ranches

How does this relate to the question of speciation? Let’s avoid a common, but likely erroneous, assumption: That speciation has a specific goal. The process of speciation in the wild is not like the process of breeding on farms and ranches. For a new species to form, the offspring do not need to reach some predetermined target or goal. Biologists don’t classify groups of animals as new species only if they possess the traits that the biologists want them to have. Instead, biologists label populations of animals as new species if they are different and isolated from other populations of animals. Thus, for our purposes, we want to know the probability of offspring looking different from their parents.

In our example, both the striped and the solid-colored offspring are different from their parents. Combined together, the probabilities of these two outcomes represent the probability of being different from the parents: 25% + 25% = a 50% chance of being different. Wow!

But let’s stop and reflect before considering the statistics of the next generation. In our current set of offspring, we do not yet have a new species. To get a new species, we need to produce a whole population of similar-looking individuals—similar to each other but different from the parents. On average,5 equids bear about 1 offspring per year, and these offspring do not reach sexual maturity until around 3 years of age. (Because of multiplicative growth, this seemingly slow start will still result in over 1 million(!) individuals in 100 years.6) For our statistics to lead to a new species, we need to produce two offspring that look different from their parents.

In fact, we need two offspring that look similar to one another—but different from their parents. If one of the offspring were striped (i.e., AA) and the other solid-colored (i.e., aa), then their offspring would simply return to the parent look—semi-striped (i.e., Aa)—and get us no further on the path towards a new species.

In other words, we need two striped or two solid offspring. The chance of this outcome is the chance of getting two of the individual outcomes in a row—it’s 25% (i.e., 1 in 4) multiplied by 25% (i.e., 1 in 4), which yields a 1-in-16 chance. But this 1-in-16 chance has two ways of being realized—i.e., with two striped offspring (a 1-in-16 chance) or with two solid offspring (a 1-in-16 chance). Together (1 in 16 plus 1 in 16), they yield a 2-in-16 chance. Based on statistics, the Ark equid pair produces two identical-to-each-other-but-different-from-parents offspring only 12.5% of the time (2/16 = 0.125). Viewed from another angle, 87.5% of the time the Ark parents would not produce a pair that could be the basis for a new species. Does this make post-Flood speciation difficult?

No. This is where the multi-generational statistical effects of genetic drift come into play. For the sake of argument, let’s say that the first offspring of the equid Ark pair was striped (i.e., AA) and that the next offspring was semi-striped (i.e., Aa), like the parents. (This type of scenario, namely, a homozygous—e.g., AA or aa—offspring matched to a heterozygous—e.g., Aa—offspring has a 50% chance of occurring.7) If these two offspring became parents, we can calculate the probabilities of their offspring with another Punnett Square:

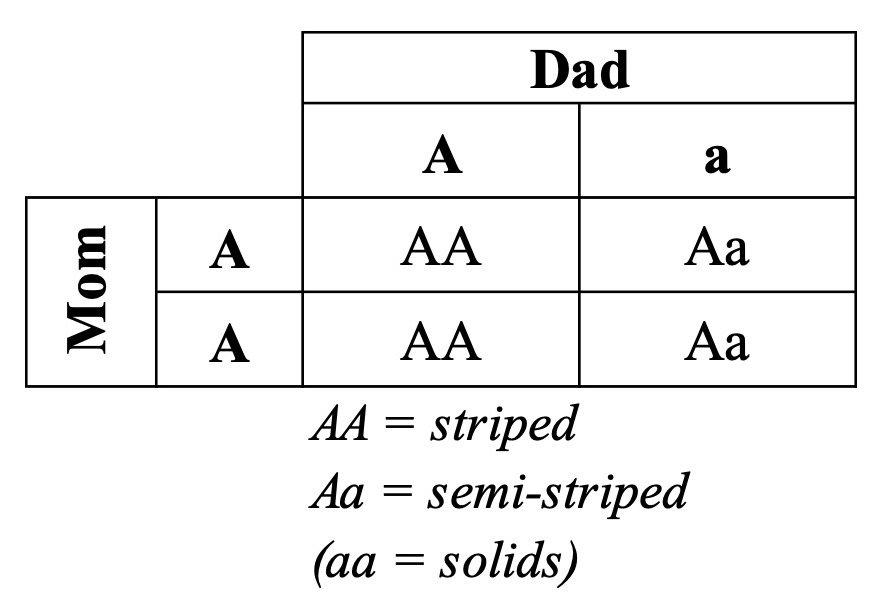
Again, the chance of their offspring looking different from the original Ark parents (i.e., the chance of getting AA offspring) is still 50%. But now the chance of getting two identical-to-each-other-but-different-from-the-original-parents offspring jumps up. Again, we multiply individual probabilities—the probability of getting a different offspring (i.e., AA) multiplied by itself. Doing so reveals that this AA and Aa mating event has a 25% chance of producing a pair that could be the basis for a new species (i.e., 1 in 2 multiplied by 1 in 2 = 1 in 4, which is 0.25 or 25%).

In just two generations, the probability of producing a pair of offspring that could lead to a new species jumped to 1 in 4.

Thus, in just two generations, the probability of producing a pair of offspring that could lead to a new species jumped to 1 in 4. Anyone playing the lottery would love to have such good odds. Conversely, if this population then became isolated from everyone else—which could easily occur as the animals spread out from Ararat over the earth, then the population would become homozygous. In other words, they would lose some of the genetic information that was present in the parents—either the A or the a information. Effectively, this would lead to a permanent change in the population, which would be recognized as a new species.

But what about the fact that we oversimplified this process? Running a more realistic scenario would simply make this process easier. More DNA differences mean more ways to produce a diversity of offspring—which means more ways to get a new species!

Rapid Origin of Species

Consider what we’ve just observed: If we have a starting population of heterozygous parents (i.e., for which multiple independent lines of evidence exist8), the fast production of new species is virtually guaranteed. At first pass, this conclusion is not easy to recognize. But that’s because it involves several small, seemingly insignificant statistical steps. Yet these small changes add up very quickly over time to produce wholesale change, which we call new species.

In a sense, the scenario we’ve just witnessed is analogous to hiking along a narrow mountain ridge (Figure 3). Let’s say the ridge represents the genetic (heterozygous) state of the Ark parents. Let’s also say the valleys on either side of the ridge represent the genetic (homozygous) state in the descendants of these parents that became new species. If you’re walking along the narrow ridge, you might occasionally step off the path by accident. With a path that is narrow, you’ll need to catch yourself and regain your balance to prevent tumbling down the hill. For every step off the path, you’ll need to exert extra effort to regain the ridge position that you had previously. In some instances, your next step might also be off the path. For each step you take off the path, the chance that you stay permanently off the path—by tumbling down the ridge—grows. A similar situation exists in the genetic scenarios we just encountered. A ridge path is hard to maintain. Tumbling down the hill is an easy path to fall into.

Figure 3. An illustration of the genetic ridgeline (Credit Gary Rogers, via Wikimedia Commons).

To increase the chance of eventually witnessing low probability events, evolutionists invoke enormous amounts of time.

Our analogy also reveals why evolutionists emphasize natural selection so much more than genetic drift. They also see new species as analogous to being in the valleys, and they see heterozygous states as being on the ridge. But, in the evolutionist’s scenario, animals don’t start on the ridge. They start in the valley. Going from the bottom of the valley to the top of the ridge—in order to go down into the next valley—requires a massive effort and many steps. And the chance of this occurring is low. To increase the chance of eventually witnessing low probability events, evolutionists invoke enormous amounts of time. More importantly, to “help” animals on their way up the ridge, evolutionists invoke natural selection. They know that dumb luck doesn’t hold much promise for crossing the ridge. Instead, they hope that natural selection will stabilize small, accidental baby steps up the ridge that an animal might take while traversing the valley. If natural selection can stabilize each accidental baby step, then perhaps the animal can eventually rise to the top of the ridge.

In theory, this explanation might seem plausible. In practice, some evolutionary pathways involve not just valleys and ridges but also chasms. Some hypothetical evolutionary intermediates exist on an evolutionary path in a valley that is separated from a ridge by a large canyon—a canyon that cannot be crossed by baby steps aided by natural selection. Rather, as any observer of a large chasm would instantly recognize, only a miraculous leap would get the animal from the valley across the chasm, from which it could potentially make its way up to the top of the ridge. Since evolution forbids miraculous leaps, such chasms demonstrate the impossibility of certain evolutionary steps.9

In summary, one of the keys to understanding the origin of species is genetic drift—the simple application of statistics to basic genetics. If Noah brought heterozygous ancestors on board the Ark, then the formation of new species—at a rapid pace—was virtually guaranteed. And if this process was virtually guaranteed, then creationists are sitting in the driver’s seat when it comes to the central question in the creation/evolution debate.