Key Flaw Found in Radioisotope Isochron Dating

North Carolina State University has recently conducted research revealing an “oversight in a radioisotope dating technique used to date everything from meteorites to geologic samples,” which means that “scientists have likely overestimated the ages of many samples.” This research was done in the university’s Nuclear Engineering Department by Associate Professor Robert Hayes and a report published in the journal Nuclear Technology.1

To claim a key flaw has been found in the radioisotope dating methodology, which underpins the millions-of-years edifice of all modern secular geology, is quite extraordinary. Such an extraordinary claim requires extraordinary evidence to back it up, and since this is a complicated subject, it requires some preliminary explanations so that the details of this claim and the evidence for it can be readily understood.

Atoms, Isotopes, and Radioisotopes

Every chemical element is made up of atoms unique to it. All atoms consist of a nucleus around which electrons (negatively-charged particles) orbit. Within the nucleus of nearly all atoms are protons and neutrons, positively-charged and neutral particles respectively.

All the atoms in each chemical element have the same number of protons in their nuclei. That number is called the atomic number of the element. Element 1 is hydrogen with one proton in its nucleus. Its chemical symbol is H. One of the heaviest elements is uranium with 92 protons in its nucleus and symbol U.

The combined number of protons and neutrons in an atom’s nucleus is called its atomic weight, because almost all the weight or mass of an atom is in its nucleus. However, the number of neutrons in the nucleus of each atom is not always the same. Often there are equal numbers of neutrons and protons, but sometimes there are more neutrons than protons.

Thus every element has atoms with the same atomic number, but its atoms can have several different atomic weights because of the different numbers of neutrons. Atoms of the same element that have different atomic weights are called isotopes of that element.

For example, carbon (symbol C) is element 6 because it has six protons in every one of its atoms. However, while most carbon atoms have 6 neutrons in their nuclei, there are a few atoms with seven and even fewer atoms with eight neutrons in their nuclei. We distinguish these isotopes of carbon from one another by their different atomic weights as carbon-12, carbon-13, and carbon-14, or in “shorthand” as ¹²C, ¹³C and ¹⁴C (see figure 1).

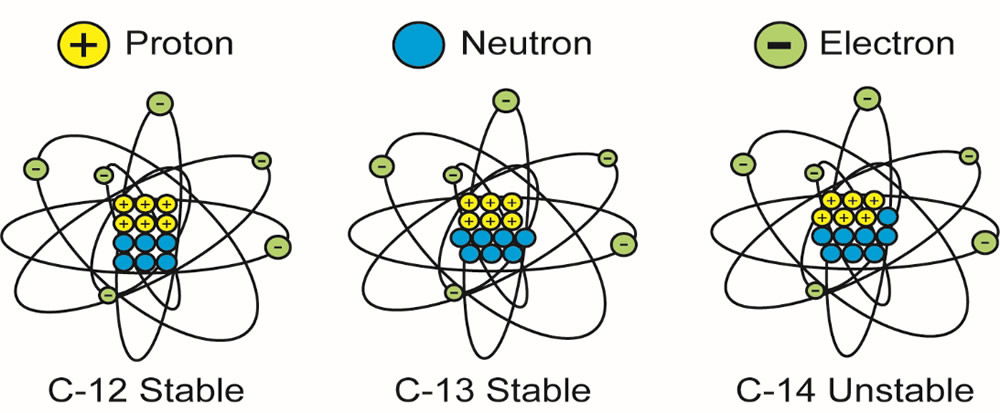
Figure 1. The three isotopes of carbon, showing their numbers of protons, neutrons and electrons.

The nuclei of ¹⁴C atoms are unstable due to their size, so they each randomly eject a portion of one of their neutrons out of their atoms. The result is different atoms, with seven protons and seven neutrons in their nuclei, and seven orbiting electrons. Those characteristics define element 7 atoms, which are stable ¹⁴N (nitrogen).

The ejected particles can be measured by suitable detectors such as Geiger counters. This process of nuclei ejecting particles is known as radioactive decay. So the unstable isotopes are called radioisotopes. Thus ¹⁴C is often referred to as radiocarbon.

Geologists and others have devised ways to use radioactive decay as a method to date rocks and dead organic materials such as bones.

Geologists and others have devised ways to use radioactive decay as a method to date rocks and dead organic materials such as bones. This method is called radioactive, radiometric, or radioisotope dating.2 The radioisotope, which decays, is often referred to as the parent isotope; while the stable isotope, which is the end result of the radioactive decay, is called the daughter isotope.

In the case of the radiocarbon dating method, we can measure the rate at which ¹⁴C decays today to ¹⁴N. If we know how much ¹⁴C was in a bone when an animal died, and we can measure how much is in the bone today, then by knowing the rate of decay we can calculate how long ago the animal died.3 Or so the theory says. It is a bit more complicated than that.4 Supposedly very ancient materials that should thus be old in evolutionary time still have ¹⁴C in them and are thus only thousands of years old.5

Isochron Dating

There is a refinement of the radiometric dating method known as isochron dating. In the case of ¹⁴C decay to ¹⁴N, and ⁴⁰K (potassium) decay to ⁴⁰Ar (argon), only single samples are required to measure the parent and daughter elements and calculate an age for the bone or rock, respectively.

However, in many rock units, such as individual granite bodies and individual basalt lava flows, many single samples can yield different Rb (rubidium)-Sr (strontium) or U (uranium)-Pb (lead) radiometric dates. This is because the different samples have different quantities of the parent radioisotopes in them.

So the isochron method was developed to use multiple samples from each rock unit to obtain a single age for it. It is argued that using multiple samples gives a more reliable result. Furthermore, the isochron method is claimed to overcome other problems with the assumptions involved in all radiometric dating techniques.6

The theory of isochron dating goes like this. At time zero when the rock unit formed (for example, the granite body crystallized and cooled), the samples of it had different numbers of parent ⁸⁷Rb atoms in them. But because the radioactive decay of the ⁸⁷Rb was just starting, the samples all had the same zero amount of daughter ⁸⁷Sr in them.

So we plot this on a graph of ⁸⁷Rb on the horizontal axis and ⁸⁷Sr on the vertical axis. At time zero, the line connecting each sample point on the graph is a horizontal line (see Figure 2). Since all the points on that line are the same zero age, the line is called an isochron (iso “same,” chron “age”), in this case the zero isochron.

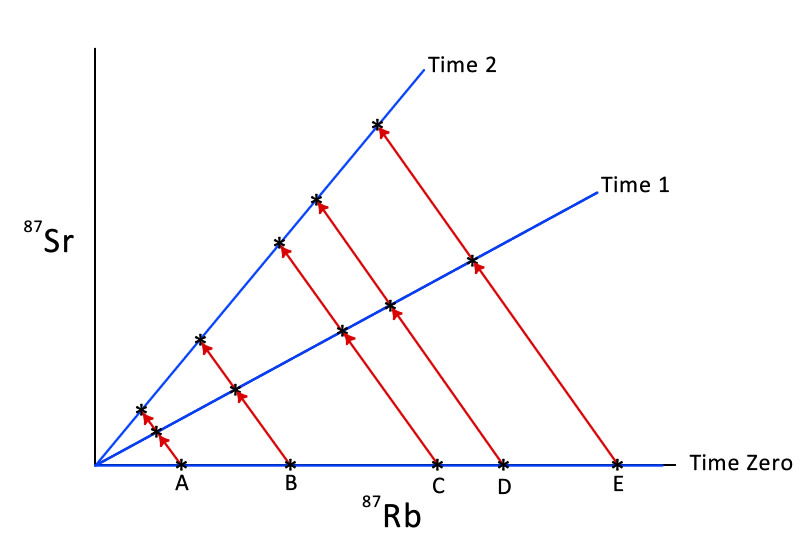
Figure 2. Five granite samples (labeled A, B, C, D and E) whose numbers of ⁸⁷Rb atoms are plotted against their numbers of ⁸⁷Sr atoms, with the resultant isochron lines at times zero, 1 and 2 as the ⁸⁷Rb decays into ⁸⁷Sr.

As time then passes, the different numbers of ⁸⁷Rb atoms decay to give different numbers of ⁸⁷Sr atoms, but in the same proportions. So at time 1, sample B with double the number of ⁸⁷Rb atoms as in sample A will contain much more ⁸⁷Sr than that in sample A. But as both samples are the same age, they will plot on the same line on the graph (see Figure 2). However, the isochron line has simply rotated upwards from time zero (horizontal) to time 1 (sloping). This is because as the number of ⁸⁷Sr atoms in each sample increases, the number of ⁸⁷Rb atoms in them decreases due to its radioactive decay.

As time passes, the different numbers of ⁸⁷Rb atoms continue to decay to give different numbers of ⁸⁷Sr atoms in the different samples, but in the same proportions. So when plotted on the graph, the samples at time 2 all fall on the time 2 isochron line (see Figure 2). Again the isochron line has simply rotated from time 1 to time 2.

As it turns out, from the math describing the isochron line, the slopes of these isochron lines equate to the ages of the rock unit at times zero, 1, and 2.

However, the analytical procedure is not as simple as measuring how many ⁸⁷Rb and ⁸⁷Sr atoms are in several samples in a granite body. First, in practice the different numbers of ⁸⁷Rb and ⁸⁷Sr atoms in the several samples don’t usually fall on a coherent line when plotted. Second, the numbers of atoms of these elements in the granite samples are very small, making accurate measurements very difficult.

The solution to both these difficulties is provided by an instrument designed for the purpose of measuring isotopes: the mass spectrometer. It can distinguish between isotopes based on their atomic weight. Furthermore, it is most sensitive to measuring isotope ratios.

The stable isotope of strontium is ⁸⁶Sr. That means the numbers of ⁸⁶Sr atoms in the granite samples don’t change as ⁸⁷Rb atoms decay to ⁸⁷Sr atoms. Thus rather than having to count the numbers of ⁸⁷Rb and ⁸⁷Sr atoms, the mass spectrometer is used to measure the ⁸⁷Rb/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios in the samples.

The isochron technique has become the best-practice standard procedure in radiometric dating of rocks.

The math in this procedure is called normalization. It actually brings the variable ⁸⁷Rb/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios into the linear relationship called the isochron whose slope can be shown to be the apparent age of the granite body. Thus the isochron technique has become the best-practice standard procedure in radiometric dating of rocks.

The Overlooked “Wrinkle!”

Now it has come to light that there is a key flaw in this methodology, which thus far has been overlooked.7 And it would have resulted in over-estimation of isochron ages.

The ⁸⁷Rb/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios are thought to be influenced only by radioactive decay of ⁸⁷Rb into ⁸⁷Sr. The whole theory of isochron dating is based, and dependent, on that seemingly reasonable assumption.

However, that assumption does not take into account differential mass diffusion—the tendency of different atoms to diffuse through materials at different rates. In this case, ⁸⁶Sr atoms can diffuse (or leak) more readily than ⁸⁷Sr and ⁸⁷Rb atoms, simply because ⁸⁶Sr atoms are smaller.

As stated by Robert Hayes of North Carolina State University, geologists dating rocks have to be sure that the differential diffusion of ⁸⁷Sr, ⁸⁶Sr and ⁸⁷Rb has not contributed to a linear distribution of the ⁸⁷Rb/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios, as in an isochron.8 Any such linear bias that might occur from this isotope diffusion effect would then have to be corrected in applying the isochron radiometric dating methodology to the isotopic ratios.

How Differential Diffusion Occurs

There are two mathematical models for diffusion through a solid. These are steady state and dynamic diffusion corresponding to the well-studied Fick’s first and second laws, respectively.9 The driving force in diffusion is a concentration gradient attempting to homogenize all substances at microscopic scales. Until the concentration gradient is allowed to taper off to closely approach zero due to the diffusion process, the diffusion of each isotopic species can be expected to follow Fick’s second law. Of course, geologists would argue the close-to-zero condition would be slowly approached over geological timescales, so up until now such diffusion has not been considered a problem to the isochron dating of rocks today.

However, the diffusion coefficient is expected to be different for each isotope for a given matrix in accordance with each’s differences in mass, chemical bonding, defect types, and concentrations.

Diffusion from and around grain boundaries can be expected to be the dominant effect when the samples being dated include grain boundaries in the rock matrix. This will be the case for all rock samples, even those from which the minerals are separated for isochron dating. All rock samples have large fractions of grain boundaries, so they will all suffer from these more egregious diffusion effects.

There are multiple approximations to account for the mass effect, beginning with the approximation that the vibrations in a crystal lattice all have the same harmonic frequencies. The atomic bonding between like atoms in a crystal having the same strength is also a good approximation, although the approximation of a mass dependence may give better overall results. In either case, the approximation of a classical spring being the atomic bond between adjoining atoms gives rise to the mass effect of the oscillation frequency. Thus the square of the vibrational frequency is inversely proportional to the isotopic mass of a diffusing atom.

A frequency distribution gives the basic mechanism driving lower mass isotopes to diffuse faster than larger mass isotopes. This means the frequency for ⁸⁶Sr vibrations is just more than 1% greater than that for ⁸⁷Sr at room temperature. Over supposed geological timescales, this should not simply be assumed to result in a negligible frequency factor without sufficiently supporting measurement verification. This becomes particularly true for samples that include large fractions of grain boundaries.

The relative scale of increasing diffusion effects in solids is smallest for vacancy diffusion followed by interstitial diffusion, with grain boundary diffusion being the largest potential mechanism when it is available. This contributes to a sample-specific isotopic mass diffusion effect, since impurities, defects, and grain boundary contributions can vary substantially within a single rock sample if granular inclusions are present.

Strontium is in the same chemical family as calcium and magnesium. On the other hand, rubidium is in the same chemical family as potassium and sodium. Those minerals that contain K or Na such as Na-plagioclase and/or K-feldspar can be expected to have higher Rb content due to the potential family substitution. Similarly, minerals that would normally contain Ca or Mg, such as Ca-plagioclase, olivine, and/or pyroxene, can be expected to have higher Sr content due again to the family substitution.

Igneous rocks are the primary targets for isochron dating, and they will contain plagioclase and sometimes K-feldspar, plus or minus other relevant minerals. Those feldspar crystals will often contain a higher Rb content than those other minerals that do not have K content.

The crystallization of igneous rocks will generally take place at different rates, depending on whether they cooled underground (granites) or at the earth’s surface (basalts). This gives rise to fractionalization of the Rb and Sr contents of the magma into the different compatible minerals at different temperatures as the rocks crystallize. Thus the mobility and solidification rates will change with temperature, setting up the initial conditions for the isotopic ratios in each mineral.

These effects give rise to a natural distribution of Rb/Sr ratios in a mineral. It is this variation that allows the linear distribution to produce isochrons which provide date estimates for rocks and their constituent minerals. The further action of radioactive decay can then result in a functional dependence, provided no further mixing within the rock takes place, such as via ground-water infiltration, crystal re-growth, or material degradation via weathering and erosion.

Solid-state diffusion can take place through multiple means. These include interstitial, vacancy, and even multi-vacancy mechanisms. This can occur on the surface of a rock, through grain boundaries, and directly through the volume of a rock (albeit much slower). The most significant of these is along the surface of the rock followed by transport along grain boundaries.

These diffusion mechanisms generally all follow a diffusion coefficient temperature dependence. When multiple diffusion mechanisms are taking place, the product of the individual diffusion coefficients leaves the overall temperature dependence unchanged. Similarly, because the diffusion is exponential, the resultant overall activation energy for the diffusion is the sum of the individual activation energies.

This isotope effect is not widely discussed in the geochronology literature (if at all). In solids, the diffusivity of one material through another still depends on mass, which means that ⁸⁶Sr will diffuse through a material faster than will ⁸⁷Rb or ⁸⁷Sr. Depending on the chemical bonding of the ⁸⁷Rb, ⁸⁶Sr should in general diffuse faster than this isotope as well. The atomic radius of Rb is 20% larger than that of Sr, making both Sr isotopes in general more diffusive. Because ⁸⁶Sr is smaller in mass than ⁸⁷Sr, ⁸⁶Sr is the more diffusive of these two isotopes. This then has the potential to create a natural isotopic distribution in a sample being dated independent of radioactive decay.

The Effects on Isochron Dates

To assess the effects of this isotope diffusion based on considering all these discussed mechanisms, Robert Hayes carefully performed numerical simulations of diffusion from a point source. Evaluating the effects of only the ⁸⁷Rb/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios, he found that the basic principles at play are the mass effect and chemical bonding related effects.

For the ⁸⁷Sr/⁸⁶Sr ratio, ⁸⁶Sr has a smaller mass, which results in the distribution of the lighter isotope being represented by a higher standard deviation parameter than that of the heavier isotope after diffusion. A similar result is also true for the ⁸⁷Rb/⁸⁶Sr ratio, although it is reasonable to expect that under unique circumstances, chemical bonding forces could provide the dominant effect in the diffusion coefficient.

There is no reason to expect in general that any of these isotopes will diffuse at the same rate through any material with time and that this effect should be considered in isotopic dating of rock samples.

The radius of Rb is larger than that of elemental Sr by approximately 15%, so that in general Sr isotopes should all diffuse measurably faster than those of Rb. However, Hayes found that the only fundamental statement that can be applied to all scenarios is that there is no reason to expect in general that any of these isotopes will diffuse at the same rate through any material with time and that this effect should be considered in isotopic dating of rock samples.

There were three different potential regimes for the magnitude of the diffusion coefficients and activation energies in Hayes’ numerical simulations. It was a requirement that the diffusion of ⁸⁶Sr was greater than the diffusion of ⁸⁷Sr due to the isotope effect on identical elements. Still, in principle, the diffusion could end up in any of the following relationships:

⁸⁶Sr > ⁸⁷Sr > ⁸⁷Rb,
⁸⁶Sr > ⁸⁷Rb > ⁸⁷Sr, and
⁸⁷Rb > ⁸⁶Sr > ⁸⁷Sr.

The most expected case is that of ⁸⁶Sr > ⁸⁷Sr > ⁸⁷Rb because of the larger atomic size of Rb relative to Sr making Sr more diffusive in general.

Assuming equal concentrations and activation energies having negligible differences, Hayes’ results produced almost linear plots. What was rather revealing though was that these could easily be mistaken for linear relationships, as in isochron lines, if only a few data points were chosen from the fifty defining each plot.

Hayes emphasized how significantly this applied to isochron dating studies, because in the dating literature it is usually normal for a geological age to be ascribed using fewer than seven data points to define the isochrons. Based on his analysis, obtaining an isochron-like linear plot is virtually guaranteed based on this differential isotope diffusion effect alone!

Not surprisingly, Hayes found that the scenario ⁸⁷Rb > ⁸⁶Sr > ⁸⁷Sr produced a negative correlation, that is, a negatively sloping linear relationship. This does not fit the reality of positively sloping isochrons produced in the natural systems in rocks. Thus because of having the largest size and mass, the chemical bonding mechanics of ⁸⁷Rb cause it not to diffuse faster than both Sr isotopes.

Nevertheless, Hayes established that almost all rock and mineral samples which are affected by differential diffusion of isotopes will have some non-linearity in the distribution of their isotopic ratios. That distribution can then be related back to the bias from this differential diffusion effect independent of the purely linear distribution caused by radioactive decay. Unless that is done, the resultant isochrons will be wrongly estimating the true ages of the rocks and minerals.

It needs to be emphasized that such differential diffusion is an inescapable reality in rocks and minerals. This is because the parent radioisotopes (⁸⁷Rb, ¹⁴⁷Sm, ²³⁸U, ²³⁵U) and their daughter products (⁸⁷Sr, ¹⁴³Nd, ²⁰⁶Pb, ²⁰⁷Pb respectively) are not the elements which form the minerals in the rocks being dated, but are merely trace elements that substitute into, or are trapped inside, the crystal lattices of those rock-forming minerals. As such they are held more loosely in the crystal lattices and thus are much more likely to diffuse than any of the major elements that are more tightly bonded to form the mineral crystals.

Hayes concluded he had demonstrated that the simplest approach to remove solid-state mass diffusion effects that would have occurred would be not to use isotopic ratios in dating samples. In other words, the isochron dating technique is faulty and misleading, so only model ages should be considered. However, it is already well established that model ages for a rock unit, being based as they are on single samples, are usually substantially scattered and thus are almost totally unreliable. So without isochron dating being as reliable as previously believed, all efforts to use radioisotopes to date rocks are highly misleading and questionable.

Two Proposed Solutions

Hayes proposed two solutions. First, the differential diffusion effects on the parent and daughter isotopes in each sample (rock or mineral) to be used in an isochron dating study should first be individually assessed and potentially quantified. Only then can such effects be removed when using the isotopic ratios in question to plot isochrons and determine the ages of the rocks and minerals.

And second, alternately, careful statistical analyses should be undertaken of the isotopic ratios obtained and of the isochrons they plot on to determine and eliminate the differential diffusion effects. Only then could the “corrected” isotopic ratios be used to plot “corrected” isochrons to obtain seemingly more reliable ages for the rocks.

But this is a very subjective approach, because such statistical tools used by the geochronology community are simply designed to weed out isotopic ratios that don’t plot tightly on an isochron line and yield what is then considered a viable age for the rock. It could be instead that the isotopic ratios which plot on the isochron are actually the ones most affected by differential diffusion, which, Hayes has demonstrated, produces linear plots resembling isochrons! Thus they are the data points that should be discarded!

Furthermore, Hayes also suggested that a rigorous statistical analysis sufficient to discriminate a linear from a nonlinear distribution is generally not possible without a much larger number of sample points, as many as thirty. Indeed, he suggested that in order to avoid a false positive, at least seven points are recommended. But the work involved in first assessing each sample for differential diffusion of its isotopes thus becomes almost prohibitive.

The only other alternative Hayes proposed is to remove the edges of the mineral grains separated for isotopic analyses before proceeding to the mass spectrometer determinations of their isotopic ratios. This suggestion is based on the premise that the two dominant components of differential diffusion occur along the surfaces of rocks and the edges of minerals, and between and along the grain boundaries. By removing the grain boundaries, one effectively removes those two dominant components of the differential isotopic diffusion that has occurred. Yet to do so for more than seven samples for each isochron determination becomes a very tedious chore. And there is no guarantee that all grain boundaries have been removed and thus the effects of the dominant differential isotopic diffusion have been eliminated.

Diffusion Not the Only Problem

While Hayes’ study is eye-opening and sounds an alarm, differential isotopic diffusion is not the only problem for radioisotope dating methods now being uncovered.

First, to determine a radiometric age one has to be sure that the decay rates of the parent radioisotopes have been accurately determined and that they have been constant through all the time since the rocks formed. The RATE project uncovered several lines of impeccable evidence that demonstrate radioisotope decay rates have not been constant in the past but were instead grossly accelerated, at least during the global cataclysmic Genesis Flood.10 Furthermore, experimental determinations over the last 60–80 years have failed to accurately determine today’s values for these radioisotope decay rates.11 Thus, without accurately known constant decay rates, these radioisotope dating “clocks” simply cannot determine the ages of rocks.

Second, during the analytical process itself these isotopes are known to fractionate according to their atomic weights.12 That is, the analytical process itself causes separation and migration of the isotopes within the samples being analysed. It is another form of diffusion according to the different masses of the isotopes. If differential isotopic diffusion has occurred in the samples before they are analysed, and further mass fractionation occurs subsequently during analyses of the samples, then the resultant measured isotope ratios can hardly be accurately reflecting the time passage of past radioactive decay.

And third, we can never be sure of the respective daughter isotope concentrations in the rocks when they formed, that is, the starting conditions.13 In the potassium-argon (K-Ar) method, it is assumed there was no daughter Ar in the rock when it formed, and thus all the Ar now measured has resulted from radioactive decay of K since the rock formed. In the case of the Rb-Sr, Sm-Nd and U-Pb methods, it is argued that the initial isotopic ratios when the rock formed can be determined from the plotted isochron lines, or the initial (common) Pb can be determined from the samples’ non-radioactive-decay-derived ²⁰⁴Pb contents. But now it has been shown how unreliable such isochrons are. And it has long been known that daughter isotopes that have not been derived by radioactive decay can be inherited from the rocks’ sources in the earth’s mantle and crust when the rocks were formed!

Conclusion

This discovery and recent presentation of differential isotope diffusion as a key flaw in radioisotope isochron dating is but one more “nail in the coffin” of these radioisotope dating methods. If differential diffusion of isotopes occurs in the rocks and minerals they contain so that plotting of their analysed isotopic ratios produces straight lines indistinguishable from isochrons, then we can never be sure that true isochrons have been obtained and thus correct isochron ages.

However, such false isochrons may also be due to further diffusion or isotope mass fractionation during the process of analyzing the samples to measure the isotope ratios that have been plotted as those isochrons. Furthermore, if we cannot be certain about the initial isotope concentrations in the rocks when they formed (i.e., the starting conditions) and we cannot be sure the decay rates have been constant since the rocks formed, then these radioisotope decay “clocks” simply cannot be used to reliably give us absolute ages for rocks.