Could a Wooden Ark Survive the Flood?

Objection: Timber Is Too Weak

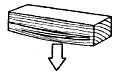
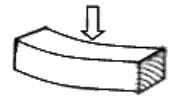
The strength of wood is a popular objection. The late 1800s saw shorter ships fail even with iron bracing. It is true that steel is superior to timber for hull construction, so steel wins for outright size. However, the size limit of timber hulls of the 1800s is a specific one, related to a particular design and outcome. Contrary to popular opinion, timber has the mechanical properties to compete with modern advanced materials when used the right way.

Clearly, timber is strong enough if the structure is suitably thick. A team of Korean naval architects and structural engineers at the world-class KRISO facility assessed the ark’s proportions for structural feasibility and seakeeping behavior.1 They concluded a 300 mm hull wall and 400 mm internal structure would make a structure adequate in waves up to 30 m (specific wave height). Modern wave data is limited to a maximum of around 11–15 m since waves beyond this size are too rare. They say wood is strong enough.

Objection: Shipbuilders in the 1800s Couldn’t Do It

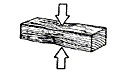
What about timber ships shorter than Noah’s ark that flexed badly despite reinforcing straps of iron? The insertion of steel straps to brace the frames against racking was certainly effective in reducing hogging and sagging flexure, but it is more a modification than a top-down design decision. The flex of the hull had been shearing the seal between planks. These ships were simply a scaled-up version of the traditional Western timber hull design, which reached a structural limit well short of the ark. But the difficulties experienced with oversized tall ships do not prove that hulls the size of Noah’s ark cannot succeed in timber. Even the method of reinforcing with iron straps is not necessarily the most effective solution for a long hull, the points of attachment between iron and wood become a new problem in this modification.

However, even this more extreme option would still be valid. The Bible clearly indicates that forged iron and bronze technology were established before the flood. Ancient civilizations such as the early Egyptians attest to early metalworking and casting skills. But even if Noah’s use of metal was restricted to spikes and some joint straps, fundamental design changes may be all that is needed to succeed in timber. It may even be possible to design a workable ark entirely of wood if such a limitation were necessary. Low-tech ideas such as layered planking and compartmentalized interior could combine to give a feasible hull of 150 m or so.

Objection: The Ark Is Too Big to Be Made Out of Timber

The ark was 300 cubits from bow to stern (Genesis 6:15). This represents a length of around 150 m.

For a timber vessel, 150 m is big, but it is about the length of a small cargo vessel today. A comparison of the ark with various ships shows it is well short of the modern supertanker but not much larger than some of the other largest timber ships on record. Noah’s ark is big but not too big.2

Objection: The Flood Was Too Rough

It is the surface of the water that affects the ark, so deep-sea tsunamis, turbulent layers of sediment, and high currents are not necessarily difficult to ride out. The fact that the ark moved about on the surface of the waters (Genesis 7:18) and later landed on a mountain of Ararat reveals that the ark survived the ordeal. The proportions of the ark seem to imply a vessel designed for the open sea, and a wind is mentioned toward the end of the flood, so there is little doubt there were waves involved. A consistent unidirectional wind is the most likely to produce big but nicely shaped waves. Hence the performance of the ark in a worst-case modern sea could be a harder test than it actually endured. The only way to get a worse sea would be to have some nearby catastrophic event such as a huge meteorite, landslide, or a powerful localized storm producing sea conditions where large waves are superimposed and irregular (rogue wave formation).

Therefore, calculations showing an ark that handles a modern sea are a valid test for the biblical ark. To believe the flood account is fictional, one must overlook the surprisingly good ark dimensions of 300 x 50 x 30 cubits, far too maritime savvy to be a mythical story appropriated by an ex-prince of Egypt (Moses, Acts 7:21) and supposedly derived from the cube-shaped vessel from the Gilgamesh epic. Additionally, it is wrong to assume that the length of the ark exceeds the size limits for a timber vessel.

Objection: Noah and His Family Were Ignorant Farmers Incapable of Building the Ark

Was the ark “mission impossible” for a bunch of ignorant farmers? Such a slur on the intellect of ancient people can hardly be justified. Not long after the flood, the Egyptians were machining granite, building the great pyramids, writing and calculating, and organizing mass labor for irrigation projects.

If civilization really did start from Noah, what would his descendants be like? “With spectacular suddenness, an architecture sprang up that was suitable for kings and gods . . . stone monuments that rank with the most impressive of any age.”3 Stone monuments endure, so everyone can see we never really got any better at it. Wooden ships decay, so there has been little evidence to confront the opinion that shipbuilding improved over time. More recent discoveries and the growth of underwater archaeology have begun to paint a different picture.

The work of early Egyptians runs counter to the evolutionary mindset.

The work of early Egyptians runs counter to the evolutionary mindset. Right from the dawn of “recorded history,” they were masters in metalwork, construction, literature, and mathematics, producing high-quality articles in granite and flint—extremely difficult materials to work with. The list goes on, and the picture is clear: these ancient people were advanced. See Ancient Technology. Likewise, other ancient civilizations had similar obsessions with monuments and grand constructions (Babylon, Greece, Maya, China, etc.). Even the ubiquitous tale of the flood seems as global as the real thing.

The explosion of civilization around 4,000 years ago is like the “Cambrian explosion” in the fossil record—an anomaly to gradual evolution but exactly what you would expect if the Bible is history. Likewise, naval architecture has not been a gradual progression but sudden, sporadic, often with periods of decline. In most cases, the development of impressive shipbuilding technology required nothing more than the right conditions—a stable government, a motive, and several centuries of development. Loss of technology is clearly demonstrated in the decline of the Greek and Roman empires and in China’s seafaring regression.

Big Ancient Ships

In support of statements like “ancient people were incapable of building the ark,” claims are made regarding the need for modern technology to make Noah’s ship function. But even the little we know of ancient maritime achievements is enough to demonstrate a potent array of maritime expertise. This includes the way they addressed the bending-induced stresses of large hulls using simple (though clever) technology.

Big boats are not a recent invention. The achievements of ancient shipwrights are impressive; however, a timber ship does not survive as does a pyramid in the desert. So our understanding of the shipbuilding expertise of ancient people is very limited. The relatively recent field of underwater archaeology has filled in much of the picture. There are two chapters of maritime history that are well known today—both indicating that large timber ships are feasible and that ingenuity and ancient technology were sufficient for the task.

Greek Trireme

The plank shear issue was more directly addressed in the ancient practice of mortise-and-tenon-jointed planks (strakes), which “goes back certainly to fourteenth century B.C. and very likely much before that.”4 There are records of an oversized trireme at 280 (Greek) cubits (Ptolemy IV 221–203 BC), or 128 m (420 ft.).5 The average trireme was well short of this scale, of course, but then the average trireme was meant to be fast in the water and light enough to be hauled up on the beach by the crew. Naturally, the enormous sizes of these ancient timber vessels were a bit hard to swallow for the modern scholar expecting to find a nice progression from the primitive dugout to The Queen Mary. They dismissed as exaggeration various accounts of oversized timber ships, including the writings of the second century AD Greek historian Athenaeus describing the Ptolemy IV vessel. The cloud of doubt evaporated somewhat when the scale of ram castings was determined from a monument that once displayed them. The sockets of the largest far surpass the skeptic’s-imposed limitation of what these ancient people could achieve.

	The oversized catamaran galley of Tessarakonteres, a three-banked catamaran galley built for Ptolemy IV 210 BC in Alexanderia, Egypt, measured 128 m (420 ft.). The dual-hull arrangement with a central working platform was designed for sea battles with catapults and could carry 4,000 marines.
	Noah’s ark, around 2400 BC, was far simpler than the racing hull of the Greek warships, but the ark was technically an oceangoing barge. To handle big waves, the hull needs to be strong, and the form somewhat streamlined.

Chinese Junks

Then there were the seagoing Chinese junks of the 1400s. Zheng He’s treasure ships had a length of 444 chi (Chinese foot) which, by the Ming gong bu chi = 137 m (450 ft.), Huai chi = 150 m (494 ft.), or at the very least a shorter shipbuilding chi = 119–124 m (390 to 408 ft.). Like most Chinese ships of the day, they were quite wide for their length—a ratio of 44:18 zhang (= 10 chi). This makes a very large vessel by anyone’s reckoning, entirely of wood with metal fastenings, and it sailed the open sea as far as Africa.6 The sheer scale of the vessels (40% longer and 65% wider, the best Western efforts) have been too much for the Eurocentric scholars with claims that the Chinese scribes were exaggerating. Some, like Richard Gould, suggest they were “a grandiose dream” or “perhaps . . . the ships . . . were built . . . but never sailed.”7 The unearthing of a rudder post in the same Ming shipyards in 1962 lends support to the credibility of the figures. The scale of the 11 m (36 ft.) long and 0.4 (1.25 ft.) diameter post was calculated using accepted formulae to a vessel length of 480 to 536 ft. “The discovery of the rudder-post shows that the Ming texts are not ‘spinning a yarn’ when they give dimensions at first sight hard to believe for the flagships of Cheng Ho’s [Zheng He’s] fleets.”8

These two cases demonstrate what can be achieved in timber. Both Greece and China were known to have used mortise-and-tenon strake jointing. In fact, the Greek workmanship was more like “furniture joinery” than the rough work of later shipwrights.9 It has been suggested that no timber ship ever repeated the technical perfection of the best triremes, which fits very nicely into the biblical worldview.

Yet the feasibility of Noah’s ark does not stand or fall on the historicity of these examples. The ark was different in many respects. However, it is worth noting that there were four separate times in history when shipwrights attempted the largest timber ship ever, and in every case, they achieved a fairly similar scale: somewhere near 400 feet long. The problems with the large ships of the late 1800s do not disqualify the ark but indicate that we are working near the limit for a timber hull. So the imagined need for steel in a hull over 300 feet might be just that—imaginary.

Appendix A: Joining Large Timbers

1. Mortise and Tenon: Timber Dowels

Mortise and tenon joints pinned together with timber dowels.

This simple joint uses the most basic materials and is the oldest method of building wooden structures, dating back at least to the early Greeks. It remained the primary method until the development of stick framing in the 1800s.

Drilling round holes in timber was never a problem in antiquity. (The ancient Egyptians even drilled granite—very well.)

But how strong is this joint? A simple calculation might give us a clue. The recommended maximum tenon is 1/3 of the thickness with hardwood dowels.

Summary of typical allowable stresses for some common sample timbers. These values are conservative.

Data	Data	Douglas Fir F8 MPa	Spotted Gum F17 Mpa
	Shear Strength (parallel to grain)	1
	Shear Stress (perpendicular to grain)	2
	Shear Stress (rolling 20% of parallel)	0.5
	Tensile Strength (parallel to grain)	8.6	17
	Tensile Strength (perpendicular to grain)	2.3
	Compression Strength (parallel to grain)	6.6	13
	Compression Strength (perpendicular to grain)	1.6	5.2
	Bending Strength (typically between tensile and comp)	8	17

2. MORTISE AND TENON—Glue

Most people are surprised to learn that aircraft wings are glued together. Of course, they use high tech adhesives and strict quality control.

The reason? Glue is the strongest—provided you have ample surface area.

What about ancient glue? The rising interest in renewable resources has brought some of the old adhesives into the spotlight. Adhesives made from lignin, soy protein, tannin, caseins, and animal blood are used today for the manufacturing of plywood, particle board, doors, etc. Since Noah was working with a lot of timber and storing large amounts of grain, he had all the ingredients he could need to produce a variety of adhesives. Furthermore, he was instructed to coat the ark (inside and out) with a substance translated as “pitch.” This might well have been a good adhesive also.

Obviously, dowels and glue should be combined. However, the glue bond would most likely break before the dowels begin to take much load, so you can’t just add the two load efficiencies together. Where adhesives would perform exceptionally well is in conjunction with layered planking.

3. INTERLOCKING TIMBER JOINTS

There are many examples of interlocking joints used in ancient structures. The problem is that so much of the cross section is taken up with the joint socket.

A joint between two members is unlikely to approach 50% of the beam strength. If three or four members are involved, then this method gets quickly out of hand. A true space frame can have 8 to 18!

4. METAL STRAPS AND SPIKES

Perhaps the only way to get close to 100% load capacity in a timber joint is to use metal reinforcing. This method would require hundreds of tons of metal to complete the ark frame.

Conclusion

There are many ways to join large timbers, but the complexity of a truss limits the options. For structural calculations where large tensile forces are likely to occur, a metal-reinforced joint appears to be the preferred choice. When a ship experiences hogging and sagging loads as a wave passes along the hull, many longitudinal truss elements would oscillate between tensile and compressive loading.

Analysis based on member properties (the strength of a beam) assumes the joint is capable of transferring the load, pointing to the metal-reinforced joint. In practice, the metal joint would be selected for the most critical joints which would be longitudinal truss elements amidships. The beams would also be made as large as possible to minimize the number of joints. Joints that are under permanent compressive loading can be treated far more simply, but with increasing wave size, such joints become harder to find.

It is not surprising that the most effective way to join timber resembles the modern roof truss connection: metal reinforcement and lots of nails.