
Noah’s Ark: Proportions of a Real Vessel
Stability, Comfort, and Strength
Somebody knew what they were doing when they came up with the dimensions of Noah’s ark. Had the ark been taller, it could become unstable; longer, and it could break; either wider or shorter, and it could become dangerously uncomfortable.
This graphic is based on the range of hull forms tested at the KRISO ship research center in Korea.1 They analyzed the Biblical proportions and found Noah’s ark to strike a balance between the conflicting requirements for stability, comfort and strength.
Koreans Study Proportions of Noah’s Ark

A Creationist group in Korea (KACR) approached a world class ship research center (KRISO) to analyze the biblical ark. Starting with the proportions given in the Bible, the KRISO team set about to compare it with 12 alternative “arks” (see below) with different proportions. By combining the requirements for stability (capsize resistance), comfort (seakindliness) and strength (hull stress), they found that is was not possible to make much improvement on the biblical ark. They assumed a random sea, where “the waves came from all directions with the same probability.” (Image KACR)
Evolutionist Heads Ark Study
The Korean tests showed that Noah’s ark had among the best proportions possible. The study was headed by Dr. Seok-Won Hong, who was principal research scientist at KRISO at the time. The study is rather clinical. For one thing, while Noah’s ark is clearly one of the top performers, it was not manipulated2 to become the outright winner in the final ranking. However, the study certainly answers any skeptic who would claim Noah’s ark is not a feasible wooden vessel.
The research paper “Safety Investigation of Noah’s Ark in a Seaway” could be viewed as an admission by antagonistic witnesses that Noah’s ark is up to the task. The fundamental “first principles” approach of the study makes an excellent foundation for further work.
Comments on the Noah’s Ark (Hong, et al.) Paper
The paper investigates a combination of three major safety parameters: structural safety, overturning stability, and seakeeping quality. Standard ship rules, computational methods, and model tests were used in the KACR-funded project at the world-class KRISO research center.
The team of nine researchers headed by Dr. Hong, Principal Research Scientist at KRISO BS, MS (Naval Architect), PhD (Applied Mechanics) also included engineering Professor S.S Na of Mokpo University handling the structural modeling of Noah’s ark.
The methodology is uncomplicated: take the biblical proportions and see what happens if they are modified. The performance of the biblical ark (300L x 50B x 30D) was compared to twelve arks of equal volume but modified by 20% and 50% in length, breadth, or depth.
The “total safety index,” the weighted average of three performances, showed that the Ark was superior in high winds and waves. Based on modern passenger ships’ criteria, it could have withstood waves greater than thirty meters.
What Do the Numbers Say?
While some of the results are not explicitly stated (e.g. wave bending moment), there is enough data to make comparisons between the various hulls. The final chart of Total Safety Index (TSI-1) excludes the stability index, so it is really only the average of seakeeping and strength indices.
Laying the data out in a single table, where;
- SK Si = Total seakeeping safety index directly from Table 2, column 1
- Struct Si = Structural safety index derived from the above graph
- Roll Si = Overturning Safety Index (moment arm) directly from Table 3. column 4.
| L | B | D | Hull front and side views | SK Si | Norm SK | Struct Si | Roll Si | Comment |
|---|---|---|---|---|---|---|---|---|
| 135 | 22.5 | 13.5 |

|
0.3575 | 0.399 | 0.15 | 0.247 | Mr average |
| 135 | 15 | 20.3 |

|
0.4125 | 0.507 | 0.10 | 1.000 | worst stability, worst bow accel |
| 135 | 18.8 | 16.2 |

|
0.465 | 0.611 | 0.11 | 0.420 | accel and roll problems |
| 135 | 27 | 11.25 |

|
0.31125 | 0.308 | 0.20 | 0.264 | similar to the Ark but weaker |
| 135 | 33.8 | 9 |

|
0.24375 | 0.175 | 0.35 | 0.412 | too low, strength issues |
| 90 | 22.5 | 20.3 |

|
0.66 | 1.000 | 0.00 | 0.222 | strongest, worst accelerations |
| 112.5 | 22.5 | 16.2 |

|
0.5475 | 0.773 | 0.05 | 0.193 | 2nd to hull #5 |
| 162 | 22.5 | 11.3 |

|
0.22875 | 0.145 | 0.40 | 0.350 | worst vertical accel, 3rd weakest |
| 202.5 | 22.5 | 9 |

|
0.345 | 0.374 | 1.00 | 0.499 | weakest, extreme vert accel |
| 90 | 33.8 | 13.5 |

|
0.45125 | 0.584 | 0.05 | 0.000 | top stability, 4th worst accel |
| 112.5 | 27 | 13.5 |

|
0.45 | 0.581 | 0.07 | 0.120 | more sedate version of #9 |
| 162 | 18.8 | 13.5 |

|
0.3025 | 0.291 | 0.27 | 0.409 | nice comfort, bit below average |
| 202.5 | 15 | 13.5 |

|
0.155 | 0.000 | 0.65 | 0.649 | best comfort, 2nd last the rest |
The ark ranks nearly average in each safety index, seventh in seakeeping, sixth in hull strength, and fifth in roll stability.
| Desc | TSK Si | Struct Si | Roll Si | TSI Ranking |
|---|---|---|---|---|
| Pure seakeeping (worst) | 1 | 0 | 0 | 12,7,4,11,3,8,0,1,10,9,2,6,5 |
| Pure strength | 0 | 1 | 0 | 5,9,6,10,1,2,0,3,11,4,7,12,8 |
| Pure stability | 0 | 0 | 1 | 9,10,6,5,0,3,7,11,4,2,8,12,1 |
Hong combines the three safety indices to get a final ranking. But how sensitive is the data to the relative weighting given to each index?
| Desc | TSK Si | Struct Si | Roll Si | TSI Ranking |
|---|---|---|---|---|
| Hong TSI-1 | 1 | 1 | 0 | 9,0,3,1,10,11,2,4,6,7,5,12,8 |
| Hong TSI-2 | 2 | 2 | 1 | 9,10,0,3,6,5,11,2,4,7,1,12,8 |
| "Equally" weighted | 1 | 1 | 1 | 9,10,0,3,6,5,7,11,2,4,12,1,8 |
| Structural emphasis | 1 | 2 | 1 | 9,10,6,5,0,3,2,11,4,7,1,12,8 |
| Capsize emphasis | 1 | 1 | 2 | 9,10,6,0,3,5,7,11,2,4,12,8,1 |
| Favor Noah’s Ark | 3.88 | 3.11 | 0.289 | 3,9,0,10,11,4,1,7,2,6,5,12,8 |
Actually, since the Total Seakeeping index was not normalized (i.e., range is not from 0 to 1 but from 0.155 to 0.6625, a range of only 0.5075), then Hong’s weighting is not really 1:1:0 or 2:2:1, but closer (yet not exactly) to 0.5:1:0 and 1:2:1, etc.
Repeating the above table using a normalized seakeeping index generally lowers the ranking of Noah’s Ark.
| Desc | Norm TSK Si | Struct Si | Roll Si | TSI Ranking |
|---|---|---|---|---|
| Hong TSI-1(n) | 1 | 1 | 0 | 3,4,7,0,11,1,9,12,10,2,6,5,8 |
| Hong TSI-2 (n) | 2 | 2 | 1 | 9,3,0,10,7,4,11,6,2,12,1,5,8 |
| Equally weighted (n) | 1 | 1 | 1 | 9,10,3,0,7,4,11,6,2,5,12,1,8 |
| Structural emphasis (n) | 1 | 2 | 1 | 9,10,0,3,6,5,11,2,4,7,1,12,8 |
| Capsize emphasis (n) | 1 | 1 | 2 | 9,10,3,0,6,7,4,11,5,2,12,8,1 |
| Favor Noah’s Ark (n) | 1.058 | 0.8 | 0.65 | 3,9,7,0,4,10,11,12,6,2,5,1,8 |
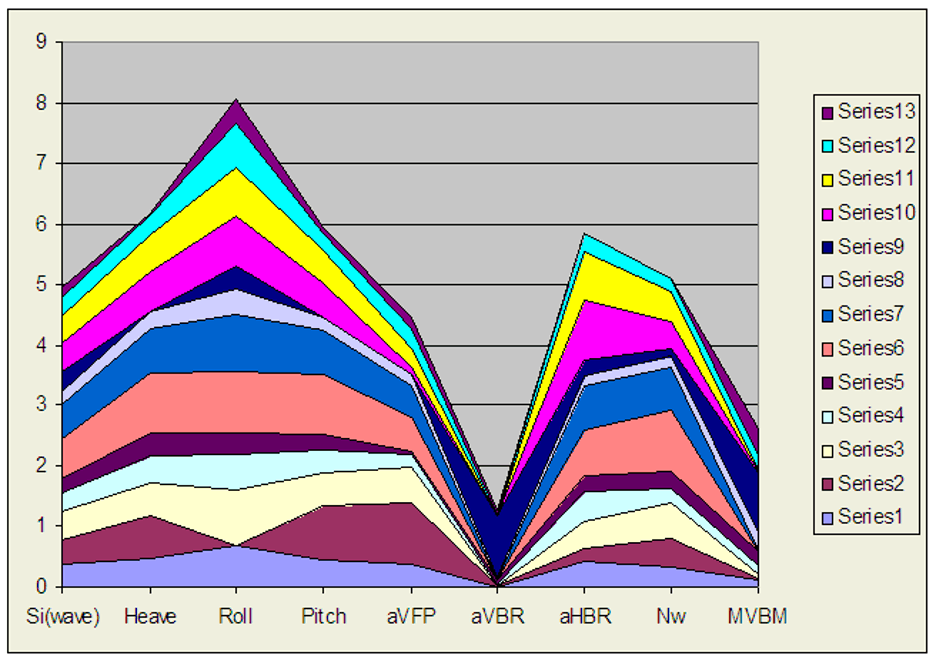
There are other weighting factors that could further influence the results. The TSK index is the sum of eight normalized seakeeping parameters— mostly accelerations of the vessel at sea: Heave, pitch, roll, vertical acceleration at bow, deck-wetting frequency, slamming frequency near the bow/stern, and the vertical and lateral accelerations in the center. Hong weighted them all equally, but alternative schemes might be just as valid. Another important point here is that this seakeeping data is for 11 m waves (H1/3), not three meters or 30 m which could also change things.
| Ship No. | Si(wave) | Heave | Roll | Pitch | aVFP | aVBR | aHBR | Nw | MVBM |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.36 | 0.49 | 0.68 | 0.45 | 0.38 | 0.01 | 0.42 | 0.33 | 0.10 |
| 1 | 0.41 | 0.69 | 0.00 | 0.87 | 1.00 | 0.01 | 0.21 | 0.48 | 0.04 |
| 2 | 0.47 | 0.55 | 0.91 | 0.58 | 0.58 | 0.00 | 0.47 | 0.57 | 0.06 |
| 3 | 0.31 | 0.44 | 0.60 | 0.36 | 0.22 | 0.02 | 0.47 | 0.24 | 0.14 |
| 4 | 0.24 | 0.38 | 0.37 | 0.26 | 0.07 | 0.06 | 0.26 | 0.31 | 0.24 |
| 5 | 0.66 | 1.00 | 1.00 | 1.00 | 0.55 | 0.00 | 0.75 | 1.00 | 0.00 |
| 6 | 0.55 | 0.72 | 0.95 | 0.72 | 0.54 | 0.00 | 0.74 | 0.68 | 0.03 |
| 7 | 0.23 | 0.27 | 0.42 | 0.22 | 0.18 | 0.07 | 0.18 | 0.20 | 0.29 |
| 8 | 0.35 | 0.00 | 0.38 | 0.00 | 0.00 | 1.00 | 0.25 | 0.13 | 1.00 |
| 9 | 0.45 | 0.67 | 0.81 | 0.56 | 0.11 | 0.00 | 1.00 | 0.45 | 0.01 |
| 10 | 0.45 | 0.63 | 0.79 | 0.55 | 0.32 | 0.00 | 0.78 | 0.49 | 0.04 |
| 11 | 0.30 | 0.30 | 0.77 | 0.29 | 0.31 | 0.02 | 0.32 | 0.21 | 0.20 |
| 12 | 0.16 | 0.05 | 0.39 | 0.07 | 0.19 | 0.09 | 0.00 | 0.00 | 0.45 |
| Table 2 (Hong). Seakeeping safety indices for a wave height H1/3 = 11 meters (safest = 0, least safe = 1). | |||||||||
Some parameters are obscured in the normalizing process by extreme figures, especially from the 50% modified hulls. For example, Hull 8 has more than 10 times the vertical acceleration of any other hull, so the normalized vertical accelerations of the other hulls are negligible. (It seems odd that Hull 8 can have the highest vertical acceleration but the lowest heave.)
A loss of aVBR contribution after normalizing with the excessive magnitude of Hull 8.
What About Hull 9?
Why is hull 9 consistently superior? It outperforms Noah’s ark in both stability and hull strength, which means that it could ride bigger waves and be easier to build. Considering that these are the usual objections to the construction of the ark (couldn’t handle the waves, too hard to make, etc.), it seems surprising that the ark does not appear to be optimized on these issues alone.
The biblical proportions are clearly adequate: Noah’s ark consistently ranks near the top in almost any weighting scheme and never below seventh place (pure seakeeping). But the extra effort required to build the longer hull seems surprising. There is certainly a lot less wood in hull 9 (and in reality, even more exaggeratedly, because space is lost to the extra wood). In most cases, hull 10 is also ahead of the biblical ark.
Even the optimal weighting of seakeeping (3.88), strength (3.11), and roll (0.289) cannot bring Noah’s ark out on top. From this information, one would think the ark should have been a little shorter. After all, lifeboats aren’t so long and skinny.
What Else Was God Thinking?
The waves of Noah’s flood are from three possible sources: tsunamis, currents, and wind. Geological evidence can give some clues about the floodwaters, such as calculating the water velocity required to transport large boulders observed in conglomerates. The dimensions of the ark itself give perhaps the best picture of the severity of the floodwaters.
Floodwater clues based on the Ark specifications:
- The ship-like proportions of the Ark
- The scale of the ark
- The fact that no other ships survived
- The assumption that the ark did not spend too much time riding critical wavelengths. Waves should be mostly bigger or smaller than the design wave for hogging, for example. The worst-case wavelength is somewhere near the length of the vessel (worst-case pitching, hull bending). Nippon guidelines give a wavelength of 140 m as the design wave in a following sea for an 18” cubit ark. The biggest waves are not necessarily the worst.
Since the ark “moved about on the surface of the waters,” wind is considered to be the most significant factor.
Hong’s seakeeping analysis assumes a confused sea: “[T]he waves came from all directions with the same probability.” Genesis speaks of a wind sent to dry the earth—a global-scale wind without interference from landforms. A consistent wind of unlimited fetch would generate mature waves, having long wavelengths and probably all in the same direction—at least from the ark’s perspective. In such a case, a longer vessel is better, provided it doesn’t end up broaching (going side-on to the waves).
The proportions God chose for Noah’s ark indicate that the waves did not come equally from all directions but had a dominant heading. The length of the ark is beyond the optimum for a confused sea, which compromises roll stability. However, by keeping a course with the wind the ark would easily outperform the shorter hulls 9 and 10 of the Hong study. Ask any mariner—ships aren’t supposed to go side-on to the waves.
The most accurate way to gauge the conditions of the flood is to look at the specifications of Noah’s ark. If the water was very calm it could have been lower: maybe two decks, which is easier. If the seas were confused, it should have been shorter. To some extent, Noah’s ark appears to have been designed for large wind-generated waves traveling almost uni-directionally with respect to the ark. However, it still has a wide enough base to handle some weather from other directions—and a smaller confused sea.
To ensure the ark does not end up side-on to the waves, the stern should drag in the water and the bow should align with the wind. The usual trick would be a sea anchor. Since the typical sea anchor in the form of an underwater sail is likely to foul with floating debris and require attention, the stern drag might be generated by protruding features of the hull itself (logs, etc). The bow would need the equivalent of a wind vane—perhaps a fin or raised area (forecastle).
The use of skegs at the stern to provide a rudder effect (somewhat akin to the fin of a surfboard) might also help to steer the vessel downwind. However, it will travel faster than a deliberately dragging stern, which may (or may not) lead to the dangerous quartering condition where the ship almost begins to “surf” with a wave. Without propulsion, this is more likely to result in a capsize risk. However, analysis is required to give an answer to this question, as well as reasonable proportions for the protrusions designed to steer the hull.
In any case, the basic principle of aligning the ark is very simple. The vessel needs to catch the wind at the bow and catch the water at the stern. This is almost the same as a badminton shuttlecock. The ball has the mass and travels under the pull of gravity—like the drive of the wind catching bow feature. The feathers drag the tail just like the drag of the stern in the water.

Shuttlecock. Leonmel42, CC BY-SA 4.0, via Wikimedia Commons
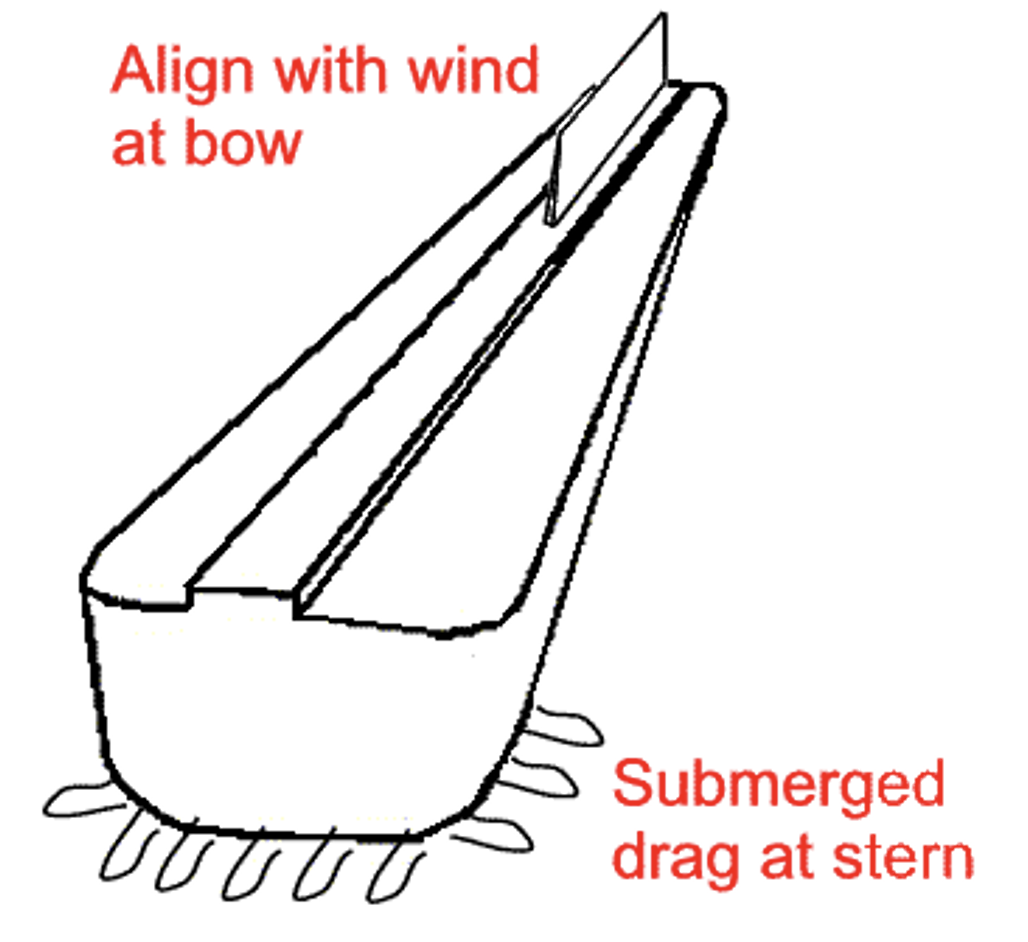
“Shuttlecock ark” using deliberate drag at the stern.
Using skegs rather than deliberate drag at the stern, the principle is more like a feathered arrow or dart. Here, gravity on the point of the dart represents the wind catching features of the bow, and the feathers represent the skeg details at the stern.

Feathered dart. Image credit: WFinch, via Wikimedia Commons
Summary of Main Points:
- The proportions and size of the ark are extremely seaworthy.
- The ark could handle 47.5 m waves before roll becomes critical.
- Timber construction using 30 cm hull and 50x50 cm frame is adequate for 30 m waves.
- The ark is 13 times as stable as the ABS rules require (for a passenger vessel).
Addendum
In the original English translation of the Korean paper, a few transcription errors were made in Table 3.
The corrected table (derived using Hong’s data only) follows:
| Ship No. | flim (degree) | AR(m.rad) | Safety Index |
|---|---|---|---|
| 0 | 31.0 | 0.805 | 0.247 |
| 1 | 53.5 | 0.321 | 1.000 |
| 2 | 40.8 | 0.694 | 0.420 |
| 3 | 22.6 | 0.794 | 0.264 |
| 4 | 14.9 | 0.412 | 0.412 |
| 5 | 42.0 | 0.222 | 0.222 |
| 6 | 35.8 | 0.193 | 0.193 |
| 7 | 26.6 | 0.739 | 0.350 |
| 8 | 21.8 | 0.643 | 0.499 |
| 9 | 21.8 | 0.964 | 0.000 |
| 10 | 26.6 | 0.887 | 0.120 |
| 11 | 35.8 | 0.409 | 0.409 |
| 12 | 42.0 | 0.649 | 0.649 |
The average absolute error between the self-corrected Ar and the Stability Calculator Ar is 0.1%
Answers in Depth
2024 Volume 19
Answers in Depth explores the biblical worldview in addressing modern scientific research, history, current events, popular media, theology, and much more.
Browse VolumeFootnotes
- The team of nine research scientists were all on staff at Korea Research Institute of Ships and Ocean Engineering (KRISO) in Daejeon, Korea. Undertaken in 1992, the results were published in Korean the following year. The paper was translated to English and published in Creation Ex Nihilo Technical Journal 8 (1):26–35, 1994. See Safety Investigation of Noah’s Ark in a Seaway.
- Despite the popular belief that science is totally objective, even the most “cut-and-dry” analysis may require some assumptions to be made. For example, in the comparative analysis of Noah’s ark, the choice center of gravity and draft is somewhat flexible (within constraints of what would be reasonable for that type of cargo). Since this study compared the relative performance of each hull, these “flexible” assumptions tend to cancel each other out. Perhaps the only place where Noah’s ark could be artificially promoted is in the choice of weighting factors for the combined stability/seakeeping/strength index. However, the outcome is not particularly sensitive to major changes to these weights. See comments above on the paper.

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- Available Monday–Friday | 9 AM–5 PM ET
- © 2026 Answers in Genesis

