A Flat-Earth Prediction Falls Flat

Introduction

Earlier this year, I published an article on the flat earth. In that article, I

• noted a sudden, rapid increase in the belief of a flat earth
• commented on possible reasons for this recent trend
• examined and refuted a few claims made by those promoting the flat earth
• gave a few reasons to believe the conventional thinking that the earth is spherical, concentrating on a few observations that anyone can carry out to show that the earth is spherical
• concluded with a testimony by Charlie Duke, a Christian and one of the twelve men who walked on the moon

Later I wrote a blog in which I refuted the claim that flat-earthers make about the apparent motion of the stars around the north celestial pole each night. I showed that the flat earth model cannot explain this motion, but that the conventional thinking explains it very easily.

In this article, I will test a prediction based upon the flat-earth model and show that the results of the test clearly contradict the prediction.

Specifics of the Flat Earth Model

In the flat earth model, the sun is 32 miles in diameter and about 3,000 miles above the earth’s surface.1 According to this theory, this rather modest sun orbits the axis of the earth’s North Pole each day (Figure 1). The sun is a spotlight that illuminates a region of the earth under this spotlight. As the sun orbits, different parts of the earth are illuminated, producing day and night. This motion also would bring the sun alternately closer and farther from each and every location on the flat earth. The sun allegedly appears to rise and then set each day as a result of perspective.2

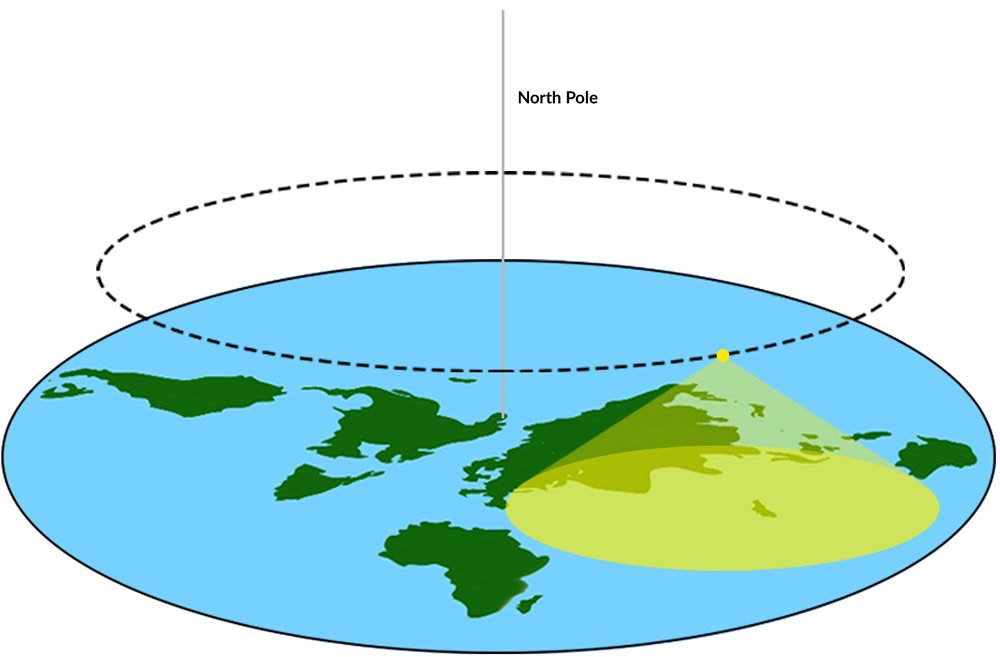
Figure 1.

This model makes some predictions. One prediction is that throughout the day the sun’s distance dramatically changes from any location on the earth, resulting in the sun appearing noticeably smaller when low in the sky compared to when it is high in the sky. In fact, some videos promoting the flat-earth theory show time-lapse movies of the sun sinking in the sky toward sunset, and, on the videos, the sun allegedly gets smaller (alternately, some videos show the same sort of thing in reverse at sunrise). For instance, in this video, the producer indicated the width of the sun’s image with parallel lines at the video’s start. As the sun approaches the horizon, its image appears to shrink. The proper explanation for this is that early in the video the sun’s light is very great, causing light to bleed into surrounding pixels. The overexposed image is larger than the true apparent size of the sun. As the sun gets lower in the sky, atmospheric extinction greatly dims (and reddens) the sun’s light. Thus right at sunset the sun’s image is not overexposed, and it more accurately portrays the correct apparent size of the sun. In the conventional model, the sun is 93 million miles away and the earth is only 8,000 miles across. Hence, the maximum possible fractional change in distance to the sun is 8,000/93,000,000 = 0.000086; this is a change of one part in nearly 12,000, so the conventional model predicts no appreciable change in the apparent size of the sun.

Quantifying the Predictions

Notice that the producer of this video (and many others like it on the internet) did not quantify how much smaller the sun ought to appear. This is not difficult to do. Let the sun be at some distance d above the earth’s surface (Figure 2). If the sun’s altitude (the angle that the sun makes with the horizon) is θ, then s, the distance of the sun from an observer, is

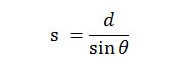
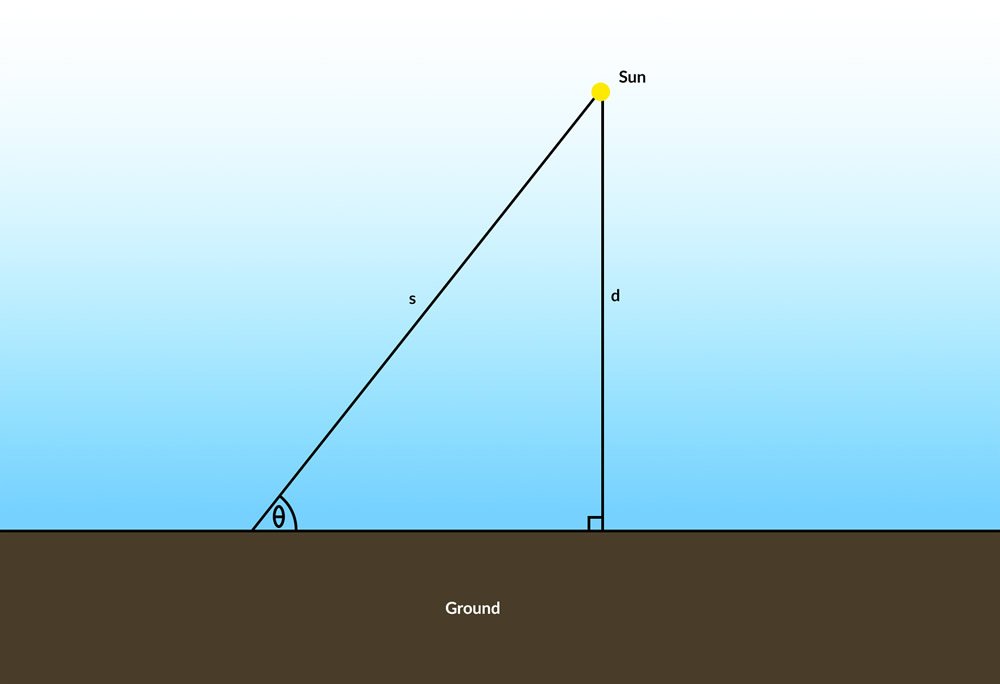
Figure 2.

Notice from either Figure 2 or this equation that, as the altitude of the sun decreases, the distance to the sun increases.

Let D be the diameter of the sun. The angular size of the sun, α (Figure 3), in radian measure, will be

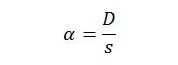
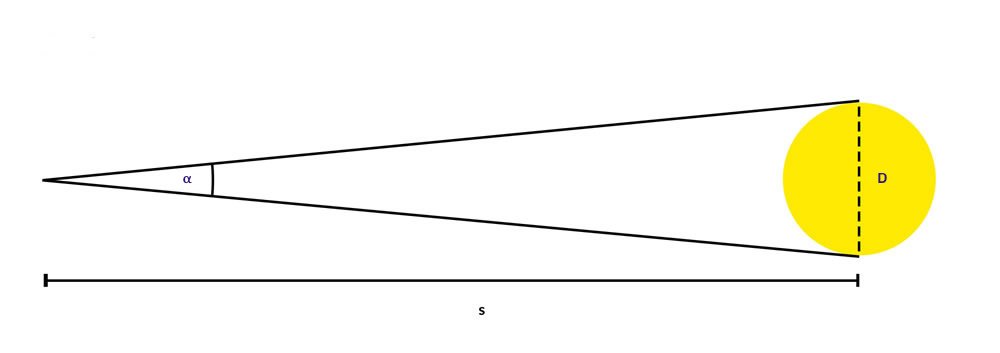
Figure 3.

Conversion to degrees is done by multiplying by 57.3 degrees, but, as I shall demonstrate, this is not necessary. Combining these two equations, we find

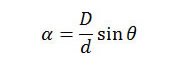
This equation is best expressed in the form of a ratio of measurements made at two different times. Let α₁ and α₂ be the sun’s angular diameters at altitudes θ₁ and θ₂, respectively, then,

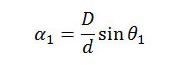
and

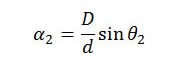
Dividing the equation for α1 by the equation for α2, the common terms in D and d cancel, leaving

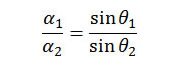
This equation is very useful for two reasons. First, it does not rely upon any particular flat-earth model, because both the sun’s size and its height above the earth factor out when expressed as a ratio. Second, because this is a ratio, there is no need to convert the angular sizes from radians to degrees.

Testing the Predictions

On Wednesday, August 3, 2016, I took photographs of the sun at Johnson Observatory on the grounds of the Creation Museum in Northern Kentucky. I shot the photos with a digital SLR camera at the Observatory’s Questar 3.5-inch telescope’s prime focus. Of course, photographing or looking at the sun is very dangerous, and neither should be attempted without a proper filter. The Questar telescope comes equipped with a very safe filter that fits on the front, preventing most of the sun’s light from entering the telescope. I took the first photograph (Figure 4) at 7:30 a.m. EDT, when the sun was at an altitude of 8 degrees. I took the second photograph (Figure 5) at 1:45 p.m. EDT. I chose the time of the first photograph because that was when the sun first rose above the trees to the east of the Observatory (a small branch of a tree can be seen silhouetted against the sun to the lower right). I selected the time of the second photograph because it was when the sun was highest that day as it transited the celestial meridian. The celestial meridian is an imaginary line that passes north-south through the zenith (the point directly overhead). When the sun passes through, or transits, the meridian, it is local noon. There are several reasons why local noon was not at twelve o’clock, the chief two reasons being that daylight-saving time was in effect, and Northern Kentucky is in the Eastern Standard Time Zone when it ought to be in the Central Standard Time Zone. The sun’s altitude at the time of the second photograph was 63 degrees. Both exposures were 1/200 of a second with an ISO setting of 200. Notice that the image of the sun on the first photograph is fainter and redder than on the second photograph. This is because of the dimming and reddening due to atmospheric extinction. I could have produced the same color and brightness by changing the exposure time and/or the ISO setting, but I wanted the settings of the exposures to be the same. Processing, such as with Photoshop, could have equalized the color and intensity of the two photographs, but neither of them were processed.

Figures 4 and 5. Photographs courtesy Danny Faulkner.

The flat-earth model and the conventional model make very different predictions about the relative sizes of the two images. Using the above equation and the angles of 8 and 63 degrees, we get

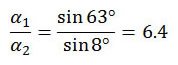
Therefore, the flat-earth model predicts that the sun’s image on the later photograph (Figure 5) ought to be 6.4 times larger than on the earlier photograph (Figure 4). On the other hand, as previously mentioned, the conventional model predicts that the images ought to be about the same size.

Examine the sizes of the sun’s image on each photograph. Notice that the images appear to be the same size. I printed the images on 8x11-inch paper and measured the horizontal diameter of the sun’s image on each photograph. The diameter on the earlier image was 237 mm, while the diameter on the later image was 240 mm. This is a ratio of 1.0126, or a difference of 1.26%. Clearly, the prediction of the flat-earth model fails, unquestionably disproving the flat-earth theory. One may object that the two images are not exactly the same size, so the conventional model is disproved too. However, the printing process is not exact due to several factors. For instance, while being printed, the paper may have stretched, compressed, or wrinkled slightly, or the feed may not have been 100% consistent. A variance of a little more than one percent is not surprising. Therefore, the conventional model is confirmed, within the errors likely inherent in the experiment.

We can take this discussion further. What would be the angular size of the sun when it is at an altitude of one degree as compared to the sun’s angular size at 63 degrees? From the equation, it ought to appear 51 times larger at 63 degrees than it would at an altitude of one degree. At one-half degree altitude, the ratio is 102. Due to atmospheric extinction, it is relatively safe on some occasions to look at the sun as it is rising or setting and has this altitude. Because many people have done this, they have some idea of how large the sun appears at the horizon. Does the sun really appear 50–100 times larger when much higher in the sky? It is interesting that those who promote the flat-earth never quantify their predictions in this manner, because if they did, their predictions would not match what we observe.

Those who promote the flat-earth never quantify their predictions in this manner, because if they did, their predictions would not match what we observe.

We can apply similar reasoning to the moon; for, in the flat-earth model, the moon is the same size and distance above the earth as the sun. Therefore, when the moon is high in the sky, it ought to appear much larger than it does when rising or setting. However, as all can easily verify for themselves, the moon does not look larger when high in the sky compared to when it is low in the sky. If anything, the moon appears larger when rising or setting than it does high overhead. This is due to the moon illusion, an effect that occurs in the brain, so is not entirely understood. Photographs of the moon when taken either high or low in the sky show no appreciable difference in size, proving that the moon illusion indeed is an illusion.

But there is a second prediction that we can test. If the earth is flat and the sun appears to set because of perspective, perspective also ought to cause both the sun and the moon to move most quickly when near the zenith and very slowly when near the horizon. We frequently observe this effect—a vehicle speeding by very close to us appears to move much faster than a vehicle far away moving the same speed. Of course, we do not observe this with the sun and moon as they rise or set. Apparently, this prediction of the flat-earth model has not occurred to its supporters.

Conclusion

In the flat-earth model, the sun is much smaller and closer to us than in the conventional understanding of the universe. Because of this vast difference in scale, the two models make specific and very different predictions about the apparent size of the sun throughout the day. The conventional model predicts that the sun’s apparent size will be the same when viewed both high and low in the sky. However, the flat-earth model predicts that the sun will appear far larger when seen higher in the sky than when the sun is lower in the sky. The results of the relatively simple experiment presented here convincingly show that the flat-earth model is not true, but are consistent with the prediction of the conventional model. Once again, I urge Christians not to be taken in by flat-earth nonsense.