
Does the North Star (Polaris) Prove the Earth Is Flat?
Is it really motionless?
Flat-earthers make two false claims about Polaris (a.k.a. the North Star, a.k.a. Alpha Ursae Minoris). One of these false claims is that Polaris remains motionless in the sky as all other stars circle it. That is the impression one gets by watching the sky over several hours. Even long exposure photographs and time-lapse videos seem to show this too. However, appearances can be deceiving.
Examining Claim Number 1: Polaris Is Motionless
The sky appears as a dome above one’s location. Since most celestial objects rise and set, it is easy to understand that what we see at any given time is just one half of a celestial sphere. There are two diametrically opposite points on the celestial sphere around which all astronomical objects spin once a day. In the conventional cosmology, these two points are the extension of the earth’s rotation axis to where it intersects the celestial sphere. We call these two points the celestial poles. Except at the earth’s equator, only one celestial pole is above the horizon. The north celestial pole is above the horizon in the northern hemisphere, while the south celestial pole is above the horizon south of the equator. Polaris is about three-quarters of a degree from the north celestial pole, so each day Polaris makes a circle in the sky with a three-quarter degree radius. That circle is too small to be readily noticed by the naked eye, and it is too small to be recorded by most photographs and time-lapse videos using standard camera lenses.
However, if one uses a lens that greatly magnifies the view (such as a zoom lens), then Polaris’ daily motion can be recorded. I have done this several times by removing the lens from a digital SLR camera and attaching it to the 127 mm f/5.2 Tele Vue refracting telescope at Johnson Observatory on the grounds of the Creation Museum. This telescope has a focal length of 660 mm, a bit more than the Nikon P900 and P1000 cameras that flat-earthers like to use. The aperture and optical quality of Tele Vue telescopes are much greater than those super zoom bridge cameras. Because of the long focal length, the field of view in the photographs is quite small, a little larger than a degree vertically in the landscape mode. Consequently, it is not possible to capture the entire circle that Polaris follows in photos with this telescope. That doesn’t matter, because it takes 23 hours, 56 minutes (the sidereal day) for Polaris to complete one circuit, and nights where I live aren’t nearly that long. Therefore, I can capture at best a little more than one-half of Polaris’ daily motion in such photos.
Rather than a single long photograph showing trailed motion, I take many short exposure photographs to produce time-lapse videos. I had done this several times for Polaris, but until recently, those time-lapse videos spanned only a few hours. I made this video from 1,165 images that I took on the night of April 14–15, 2022. I attached my Nikon D5600 digital SLR camera to the telescope. This camera is programmable, which allows me to take photographs even while I am asleep. Each photograph is a 13-second exposure with ISO 200. For proper noise reduction, each photograph was followed by a 13-second dark image, and I placed a 15-second delay between each photo, so the recorded images were spaced 42 seconds apart. The time-lapse video spans ten hours, starting in evening twilight and ending in morning twilight. The sky background is brighter than I would have liked, with the moon nearly full (astronomical full moon was about 36 hours later), along with the brightness of the lights of suburban Cincinnati. Polaris is the brightest star in the video.
Early in the video, you will see the lights of an airplane that passed through the field of view. A couple of times later in the video, the background became very bright, and the stars blurred a bit. That was due to thin clouds passing through. The clouds dimmed the stars and made them fuzzy, and the bright moon and city lights illuminated the clouds, making the background bright. Toward the end of the video, you will see a slight jump in Polaris’ motion. This was caused by a small gap of a few minutes in which the battery ran down, whereupon I changed the battery. As you can see, Polaris moved in nearly half of a circle in this video. Therefore, flat-earthers are wrong when they claim that Polaris remains motionless.
How do flat-earthers respond to this evidence? Probably no flat-earthers have seen this video yet, but a few flat-earthers have seen an earlier, shorter time-lapse videos of Polaris that I had made. For instance, Bob Knodel, a flat-earther whose work I have criticized before, saw one of my earlier, shorter Polaris time-lapse videos that I showed during a recent interview. The next day, Bob responded to the interview in his weekly podcast. Bob and the panelists on his show identified what they thought were several flaws in the video. If Bob had listened to more of the interview and shared with his friends what I had said about the time-lapse video, they would have heard me discuss what they thought were flaws but weren’t. Bob also opined that the star I identified as Polaris was not Polaris. He didn’t say what star it was, but that it just wasn’t Polaris. This is a common tactic of flat-earthers—deny all evidence that contradicts what they have chosen to believe.
Examining Claim Number 2: Polaris Has Always Been the Pole Star
The second false claim flat-earthers make about Polaris is that Polaris has always been the pole star and always will be. This is false because an effect called the precession of the equinoxes slowly but continually changes the position of Polaris in the sky. What response do flat-earthers have to this fact? They generally deny it. For instance, in my recent interview that Bob Knodel criticized, I discussed Polaris’ slow change in position over the centuries. In response to precession, Bob asserted “We’ve never recorded that.”1 Of course, Bob gave no supporting evidence for his assertion. Bob also claimed the Antikythera device from 2,000 years ago shows Polaris “to be exactly where it is today,” again with no evidence to support his claim. Bob went on to claim without substantiation that “all ancient cultures showed Polaris in exactly the same part of the sky” and asked how I explain that. Bob answered his own question with “You don’t; you lie about it.” Let’s check Bob’s assertion about ancient cultures and his claim there is no evidence for precession of the equinoxes.
Hipparchus
Hipparchus is generally credited with discovering precession of the equinoxes in the second century BC. Hipparchus measured the positions of about 850 stars and compiled them into a star catalog. Before I discuss how Hipparchus discovered precession of the equinoxes, I must discuss two of the coordinate systems astronomers use in the sky. They are similar to latitude and longitude on the earth. Being on spheres, these coordinate systems use two poles and a reference great circle arc halfway between the poles. On earth, the poles are the north and south poles, and the reference great circle arc is the earth’s equator. Latitude is measured north and south of the equator. Meridians of longitude are perpendicular to the earth’s equator. Since all meridians are equivalent, there is no obvious zero point for longitude, so geographers arbitrarily assign zero degrees longitude as passing through Greenwich, England, and all other meridians of longitude are measured with respect to this prime meridian.
The equatorial system is one coordinate system astronomers define in the sky. It uses the north and south celestial poles and the celestial equator halfway between the two poles as its reference. The north celestial pole is directly above the earth’s north pole, the south celestial pole is directly above the earth’s south pole, and the celestial equator is directly above the earth’s equator. Like latitude, declination is measured north (+) and south (-) of the celestial equator. Right ascension is similar to longitude on the earth. The prime meridian of right ascension is the meridian passing through the vernal equinox, with right ascension increasing eastward. Today, the equatorial system is the most common astronomical coordinate system because it spins with the stars each day. To remain motionless in the sky, Polaris must have a declination of exactly 90 degrees. As we shall see, this is not the case.
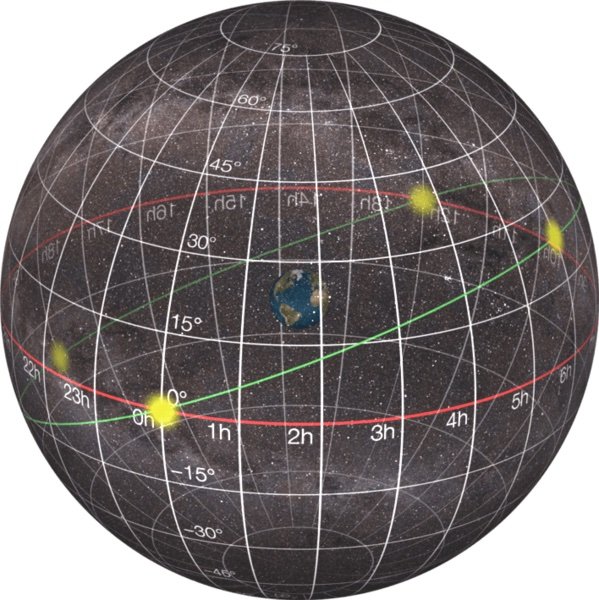
Equatorial system, by ChristianReady via Wikimedia Commons Wikimedia Commons.
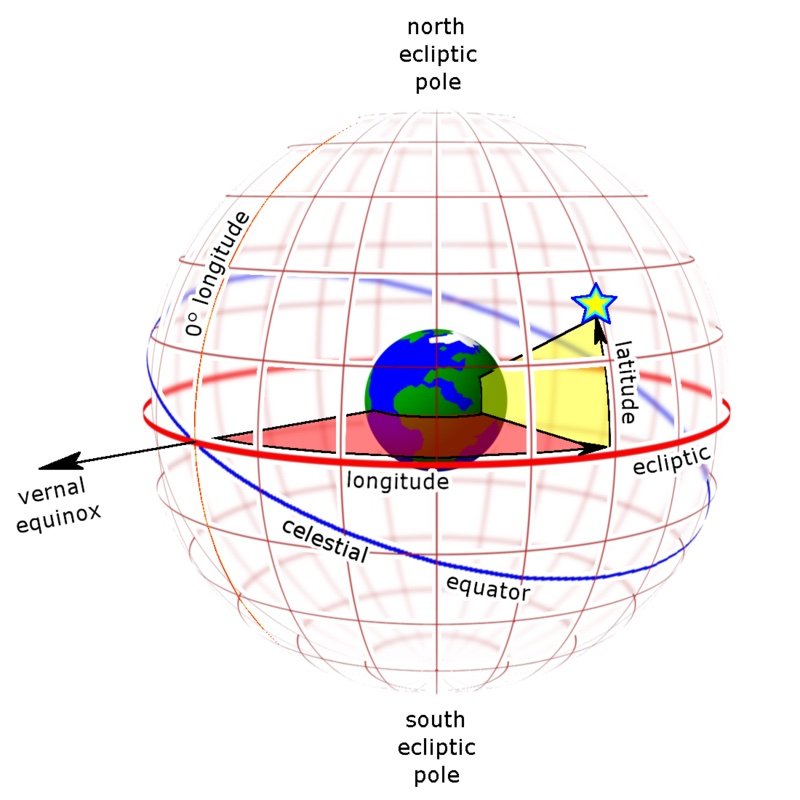
Ecliptic system, by Tfr000 via Wikimedia Commons.
The ecliptic coordinate system uses the ecliptic, the plane of the earth’s orbit, as its reference great circle arc. The extension of an axis perpendicular to the ecliptic defines the north and south ecliptic poles. Like latitude on earth, ecliptic latitude is measured north (+) or south (-) of the ecliptic. Meridians of ecliptic longitude are measured eastward from the vernal equinox.
While the north celestial pole currently is close to Polaris, this hasn’t always been so.
Due to a torque produced by the sun’s gravity, the earth’s rotation axis turns, or precesses, over a calculated 25,900-year cycle. Thus, the celestial poles spin around the ecliptic poles once each precession cycle, with a radius equal to the earth’s axial tilt (currently 23.4 degrees). Since the stars are unaffected by this change in the direction of the earth’s rotation axis, the north celestial pole slowly moves through the stars. While the north celestial pole currently is close to Polaris, this hasn’t always been so.
Precession of the Equinoxes
Hipparchus measured the ecliptic longitude and latitude of the bright star Spica, and he compared his measurement to those of Timocharis and Aristullus, made about 150 years earlier. Hipparchus found that while the ecliptic latitude of Spica had not changed, its ecliptic longitude had shifted by about two degrees. Furthermore, Hipparchus compared the lengths of the tropical year (the orbital period of the earth with respect to the vernal equinox) and the sidereal year (the orbital period of the year with respect to the stars), and he found a slight difference that was consistent with the change of Spica’s ecliptic latitude over one-and-a-half centuries. These two lines of evidence indicated that the equinoxes were sliding along the ecliptic at a rate of at least one degree per century, which is why we call this effect the precession of the equinoxes. The actual rate is about 1.39 degrees per century but given the accuracy of the measurements used and the relatively short baseline, Hipparchus’ estimation was close to the correct value. The rate of 1.39 degrees per century is about 50 arcseconds per year.
Precession of the equinoxes leaves the ecliptic latitudes of stars unchanged, so the effect of precession on ecliptic coordinates is solely a shift in ecliptic longitude. The effect of precession upon right ascension and declination is more complicated—it changes both right ascension and declination. This is problematic because we point our telescopes using right ascension and declination, making it necessary to update, or “precess,” coordinates. For instance, coordinates now are often expressed as what they were in the year 2000 (we say that the epoch is 2000). To find what the coordinates are at the current epoch (the year in which one is observing), one must precess the coordinates expressed at a different epoch to the current epoch. The conversion formulae involve trigonometric functions. Years ago, I did many precession computations with my handheld calculator. Fortunately, most research observatories now have computers that control where their telescopes are pointing, and those computers will precess the coordinates for us. There also are online resources that can precess coordinates for us (for instance, here is one).
Ptolemy
Hipparchus’ star catalog is lost, but we have Ptolemy’s star catalog. Working in Alexandria, Egypt, around AD 140, Claudius Ptolemy compiled a catalog with more than a thousand stars. This is part of Ptolemy’s great work on astronomy, The Almagest. Ptolemy’s star catalog lists the ecliptic longitude and latitude of each star. To see how close Polaris was to the north celestial pole at the time of Ptolemy, all one must do is convert Ptolemy’s coordinates to equatorial coordinates. The compliment of the declination will be the angular distance from the north celestial pole. For the conversion, I used the Clear Sky Tonight online utility.2 For the date, I used a recent date. The major factor involving the date is that the earth’s tilt changes slightly with time too. Using the wrong date doesn’t matter for our purposes because the difference caused by slight changes in the earth’s tilt over the time interval is much less than the effect of precession on Ptolemy’s data. Furthermore, expressing the angular distance from the north celestial pole to within a tenth of a degree is sufficient for our purposes.
It is easy to find the star we now call Polaris in Ptolemy’s catalog because Polaris is the first star listed. Ptolemy gave the ecliptic latitude of Polaris as +66 degrees, and the ecliptic longitude as one-sixth of a degree in the twins (Gemini).3 It took me a little while to figure out how to convert this to our modern way of expressing ecliptic longitude. At the time of Ptolemy, the vernal equinox was in the constellation Aries. Even though precession since then has moved the vernal equinox about one zodiacal sign westward, we astronomers still sometimes call the vernal equinox “the first point in Aries.” The symbol for the vernal equinox, ^, comes from the association with Aries (see the ram’s horns?). Each zodiacal sign stretches 30 degrees along the ecliptic (360 degrees/12 = 30 degrees). Since Gemini is the second sign after Aries, then one must add 60 degrees to get the ecliptic longitude of any star in Ptolemy’s catalog at the epoch of Ptolemy. Doing this for Polaris, I get 60.1 degrees (expressing the ecliptic longitude as decimals of degrees rather than in degrees, minutes, and seconds).
When I converted this ecliptic longitude and latitude of Polaris into the equatorial system using the link above, I got a right ascension of 23 hours, 16 minutes and a declination of +78.1 degrees. That is, at the time of Ptolemy, the star we call Polaris was nearly 12 degrees from the north celestial pole. That is hardly a pole star. This was about 2,000 years ago. Ptolemy qualifies as an ancient source, so Bob Knodel’s claim that “all ancient cultures showed Polaris in exactly the same part of the sky” is demonstrably false. How would Bob respond to this information? I expect that Bob would denounce The Almagest as a forgery (Jeran, a member of Bob’s program panel, opined that all sorts of ancient sources, such as Aristotle and Plato, are fakes from the 1600s and 1700s).
Copernicus
Nicholas Copernicus is generally credited with introducing the heliocentric model in his 1543 book, De Revolutionibus. But Copernicus’ book contained far more. For instance, his book included Ptolemy’s star catalog with remeasured ecliptic coordinates. Rather than expressing ecliptic longitude from the vernal equinox at the epoch of Copernicus, Copernicus expressed the ecliptic longitude of each star in reference to the star in Ptolemy’s catalog, of which was listed first in the constellation Aries. Copernicus explained why he chose to express ecliptic longitudes of stars from a reference star rather than the standard of the vernal equinox—he wanted a coordinate system fixed to the stars rather than the celestial equator.4 This explanation precedes the star catalog in Copernicus’ book.
Nicholas Copernicus is generally credited with introducing the heliocentric model in his 1543 book, De Revolutionibus. But Copernicus’ book contained far more.
How can one convert the ecliptic longitudes in Copernicus’ catalog in terms of the vernal equinox at Copernicus’ epoch? Copernicus gave specific numbers that allow this conversion.5 Copernicus explained his measurements of Spica made in Frauenburg (today Frombork) in AD 1525 and the reduction of those measurements. Copernicus found that Spica was 17 degrees, 21 minutes from the beginning of Libra. That corresponds to 197 degrees, 21 minutes ecliptic longitude. Ptolemy tabulated Spica in his catalog as being 26 and two-thirds degrees from the beginning of Virgo. This corresponds to 176 and two-thirds degrees ecliptic longitude. The difference between these two is 20 degrees, 14 minutes. This is about the amount of shift in ecliptic longitude expected from the known rate of the precession of the equinoxes at a rate of 50 arcseconds per year. Therefore, adding this difference to the ecliptic longitude of any star in Copernicus’ catalog will produce the ecliptic longitude of that star in the epoch of AD 1525. Using Ptolemy’s ecliptic latitude of 66 degrees (it doesn’t change) and putting these into the online conversion algorithm I linked above, I get a declination for Polaris of 86.1 degrees at the time of Copernicus. This is nearly four degrees from the north celestial pole. Therefore, four centuries ago, Polaris made a circle having a radius of four degrees around the north celestial pole.
Copernicus included the measurement of the position of Regulus by Al-Battani (c. AD 900), probably the greatest Muslim astronomer of the Middle Ages. Using the same approach as I did for Spica in Copernicus’s epoch, I found the declination of Polaris around AD 900 was 82.5 degrees at the epoch of Al-Battani. Therefore, 1,100 years ago, Polaris made a circle of 7.5 degrees around the north celestial pole. These data, 10 degrees from the pole 2,000 years ago, 7.5 degrees from the pole 1,100 years ago, and 4 degrees from the pole 500 years ago show that Polaris has been slowly approaching a place in the sky that eventually would earn it the title of the pole star.
But we don’t have to rely upon ancient or medieval sources to see precession for ourselves. Polaris’ 50” change in ecliptic longitude per year shows up each year in the equatorial coordinates of Polaris. I recently acquired copies of The Astronomical Almanac in 1981–1994. Section H of The Astronomical Almanac lists the positions of stars in the Bright Star Catalog. Here are the right ascension and declination of Polaris from the copies of the Astronomical Almanac that I have:
| Epoch | Right Ascension | Declination |
|---|---|---|
| 1981.0 | 02h 12m 41.5s | 89° 10ʹ 41ʺ |
| 1982.0 | 02h 13m 36.1s | 89° 10ʹ 58ʺ |
| 1983.0 | 02h 14m 31.2s | 89° 11ʹ 15ʺ |
| 1984.5 | 02h 15m 54.6s | 89° 11ʹ 39ʺ |
| 1985.5 | 02h 16m 51.3s | 89° 11ʹ 56ʺ |
| 1986.5 | 02h 17m 48.6s | 89° 12ʹ 12ʺ |
| 1987.5 | 02h 18m 46.6s | 89° 12ʹ 29ʺ |
| 1988.5 | 02h 19m 45.2s | 89° 12ʹ 45ʺ |
| 1989.5 | 02h 20m 43.7s | 89° 13ʹ 02ʺ |
| 1990.5 | 02h 21m 43.7s | 89° 13ʹ 18ʺ |
| 1994.5 | 02h 25m 50.4s | 89° 14ʹ 23ʺ6 |
As you can see, in that time interval, Polaris’ declination was slowly increasing, bringing it closer to the north celestial pole (exactly 90°). Wikipedia entries for individual stars gives positions in epoch J2000. Here is the J2000 position of Polaris from Wikipedia:7
| Epoch | Right Ascension | Declination |
|---|---|---|
| 2000.0 | 02h 31m 49.09s | 89° 15ʹ 50.8ʺ |
This is about 44ʹ (almost three-quarters of a degree) from the north celestial pole. The current position of Polaris as of April 18, 2022 is slightly closer to the north celestial pole:8
| Epoch | Right Ascension | Declination |
|---|---|---|
| 2022.3 | 02h 31m 47s | 89° 15ʹ 50ʺ |
Finally, my copy of Norton’s Star Atlas, 15th edition, printed in 1969, gives the 1950 coordinates of Polaris.9
| Epoch | Right Ascension | Declination |
|---|---|---|
| 1950 | 01h 48m 08s | 89° 02ʹ |
That is, 72 years ago, Polaris was nearly a degree from the north celestial pole.
To be exactly at the north celestial pole and truly remain motionless throughout the night, a star must have a declination of exactly 90 degrees. Polaris has never had that declination, and it never will. When will Polaris be closest to the north celestial pole? According to researchers C. H. Smiley, and Kahn A. Majid, Polaris will be closest to the north celestial pole in about 80 years (2102), when it will be a little less than a half degree from the north celestial pole.10
As you can readily see, the right ascension and declination of Polaris noticeably changes over just a few years, much less than a human lifetime.
As you can readily see, the right ascension and declination of Polaris noticeably changes over just a few years, much less than a human lifetime. Anyone using setting circles on a telescope to find faint objects such as galaxies must account for precessional changes. And it is not just the thousands of professional astronomers around the world who do this—many hundreds of thousands of amateur astronomers know about precession and make corrections to accurately point their telescopes. Hence, people do not need to take the word of professional astronomers that precession is real; anyone can verify the reality of precession if they bother to properly research the topic.
Conclusion
I have demonstrated how two claims that many flat-earthers make about Polaris are false. First, with a time-lapse video, I have shown that Polaris does not remain motionless throughout the night but rather goes through a small circular motion around the north celestial pole. Second, using historical data and modern data, I have demonstrated that Polaris has not always been the pole star. It was shortly after Copernicus that Polaris was close enough to the north celestial pole to be called “the pole star,” or in Latin, Stella Polaris, from which we get the relatively modern name Polaris for this star. These two false claims that flat-earthers repeat about Polaris do nothing to support their belief that the earth is flat, so flat-earthers could readily abandon them, if they wanted to.
Answers in Depth
2022 Volume 17
Answers in Depth explores the biblical worldview in addressing modern scientific research, history, current events, popular media, theology, and much more.
Browse VolumeFootnotes
- “Imagineering Space,” https://www.youtube.com/watch?v=kI4jcGmuZoU. Quotes from this broadcast in this article are around 1:26:00–1:28:00.
- “Astronomy Calculator,” Clear Sky Tonight, accessed May 4, 2022, clearskytonight.com/projects/astronomycalculator/coordinate/ecliptic_equatorial.html.
- Claudius Ptolemy, The Almagest.
- Nicholas Copernicus, “Book II, Chapter Fourteen,” On the Revolutions of the Heavenly Spheres, trans. A. M. Duncan (Norwalk: The Easton Press, 1999).
- Nicholas Copernicus, “Book III, Chapter Two,” On the Revolutions of the Heavenly Spheres, trans. A. M. Duncan (Norwalk: The Easton Press, 1999).
- United States Naval Observatory and Her Majesty’s Nautical Almanac Office, “Section H—Bright Star Catalog,” The Astronomical Almanac, (1981–1994).
- “Polaris,” Observation Data, Wikipedia, last modified April 30, 2022, https://en.wikipedia.org/wiki/Polaris.
- “Polaris (Star),” Guides to the Night Sky, In-the-Sky, accessed April 18, 2022, https://in-the-sky.org/data/object.php?id=TYC4628-237-1.
- Arthur P. Norton and James Gall Inglis, “Coordinates of Polaris,” Norton’s Star Atlas and Telescopic Handbook, (Edinburgh: Neill & Co., 1959).
- C. H. Smiley, and Kahn A. Majid, “Polaris and Precession,” Journal of the Royal Astronomical Society of Canada 53, (December 1959): 249, https://articles.adsabs.harvard.edu/full/seri/JRASC/0053/0000251.000.html.
Recommended Resources

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- © 2024 Answers in Genesis







