
Significance of Highly Discordant Radioisotope Dates for Precambrian Amphibolites in Grand Canyon, USA
Abstract
The Brahma amphibolites of the Precambrian crystalline basement of Grand Canyon were originally erupted as basalt lavas and subsequently suffered high-grade regional metamorphism. Composed predominantly of hornblende with minor subordinate plagioclase, the collected samples showed no signs of post-metamorphic alteration. K-Ar radioisotope analyses yielded a wide range of model ages, even for adjacent samples from the same outcrop of the same original lava flow. No statistically viable K-Ar isochron age could be obtained because of so much scatter in the data, which is most likely due to 40Ar* mobility within these rocks. By contrast, the Rb-Sr, Sm-Nd, and Pb-Pb radioisotope systems yielded good, statistically consistent, isochron ages of 1240 ± 84 Ma, 1655 ± 40 Ma, and 1883 ± 53 Ma, respectively. These are obviously discordant with one another and with published ages, but there are no clear reasons to reject any of them as unreliable or invalid. One explanation for the discordance is that the decay rates of the parent radioisotopes were different relative to their presently measured rates at some time during the time interval since these rocks formed. We observe that the a-decaying U and Sm yield older ages than the ß-decaying Rb, and the heavier atomic weight U yields a Pb-Pb age older than the Sm-Nd age. This pattern in the discordances thus may provide clues into the physics responsible for time variations in the decay process. Obviously, if decay rates have not been constant, radioisotope decay methods do not yield valid absolute ages for rocks.
This paper was originally published in the Proceedings of the Sixth International Conference on Creationism, pp. 407–424 (2008) and is reproduced here with the permission of the Creation Science Fellowship of Pittsburgh.
Keywords: Grand Canyon, Precambrian crystalline basement, Brahma amphibolites, hornblende, plagioclase, whole-rock chemical analyses, whole-rock K-Ar model ages, whole-rock Rb-Sr, Sm-Nd, and Pb-Pb isochron ages, discordancy, accelerated radioisotope decay, half-lives, mode of decay, atomic weights
Introduction
The assumption of constant radioisotope decay rates has undergirded the interpretation of all radioisotope data and the establishment of the absolute dates in the uniformitarian geologic timescale. Anomalous radioisotope dates that do not fit the chosen timescale are usually explained by open-system behavior and/or inheritance, and then discarded. Because most anomalous radioisotope dates are not published, it is difficult to know just what proportion of dating analyses in geochronology laboratories are discarded. Furthermore, rock samples are often only dated using the one radioisotope method. Thus, it is difficult to quantify just how significant are the few multiple radioisotope concordances published in the literature, and how reliable and consistent is the apparent overall trend of progressively decreasing dates from lower strata in the geologic record through to upper strata. However, the impression gained from a detailed examination of the primary radioisotope dating systems1 is that, if the absolute dates of the uniformitarian timescale were ignored, and both accepted and anomalous radioisotope dates were considered, where more than one radioisotope system has been utilized to date specific rock strata, radioisotope discordances would be in the majority. That such discordances are often the case has already been discussed,2 and has been thoroughly tested and documented on some specific strata.3, 4, 5, 6
Furthermore, it is highly significant that there are no obvious geologic or geochemical explanations evident for these discordances.7 Thus, if it weren’t for the assumption that the approved radioisotope dates are acceptable because they correlate with the conventional uniformitarian timescale, then all the discordant isochron ages could actually be anomalous. Using the same reasoning, therefore, there is no guarantee that even where radioisotope concordances do occur the resultant dates are somehow objectively correct. In any case, the ages derived from the radioisotope systems should only be regarded as maximum ages. The prolific evidence of open-system behavior and mixing and/or inheritance suggests that the true ages of the strata may be considerably, or even drastically, younger. This is intolerable for uniformitarians, as their evolutionary timescale is crucial to their paradigm. These endemic problems with the radioisotope dating methods demonstrate that the conventional interpretation of radioisotope dating is not secure, and also provide evidence that indicates a much younger earth.
A very relevant example is the stark contrast between the U-Pb radioisotope age of 1500 Ma for the zircon grains in the Jemez granodiorite of New Mexico and the He (derived from U decay) diffusion age of the same zircon grains of only about 6,000 years.8, 9, 10, 11 This huge discrepancy can be explained if the rate of 238U decay was grossly accelerated at some time(s) in the past. A proposed test of this explanation is to document whether there is a systematic pattern in the discordances between the different radioisotope systems. If there is a systematic pattern, it may reflect differing amounts of such accelerated nuclear decay in the different radioisotope systems over the same real time interval, due to their different modes of decay and parent half-lives.12 The amphibolites in the Precambrian basement of the Grand Canyon were chosen for this study for three reasons. First, the Grand Canyon is a well known and well studied area that contains a good, clear strata cross-section representative of much of earth history. Second, as metamorphosed basalts, amphibolites consist of a very simple two-component system, essentially just the minerals plagioclase and hornblende, which simplifies the geochemistry of radioisotope systematics. And third, being Precambrian, these rocks should have accumulated large enough amounts of the radioisotope decay products to produce isochrons with good statistics.
Geology of the Precambrian Basement Metamorphics in Grand Canyon
The east-west trending Grand Canyon presents spectacular exposures of the Lower Proterozoic (Paleoproterozoic) rocks of the crystalline basement beneath the Colorado Plateau.13 In the Upper Granite Gorge, these rocks are continuously exposed from river mile 78 to 120 (downstream from Lees Ferry), while there are discontinuous exposures in the Middle Granite Gorge from mile 127 to mile 137 (fig. 1).14, 15 Powell was the first to identify the Precambrian “granite” and “Grand Canyon schist.”16 Walcott identified Significance of Highly Discordant Radioisotope Dates for Precambrian Amphibolites in Grand Canyon, USA the Vishnu “terrane” as a complex of schist and gneiss.17 Subsequently, Campbell and Maxson identified different mappable units called the Vishnu “series”18 and Brahma “series”.19 However, Campbell and Maxson20 underestimated the structural complexities and probably overestimated the stratigraphic thickness when they proposed that the combined stratigraphic sequence of these metasedimentary and metavolcanic rocks was 8–16 km thick. This stratigraphic approach was called into question by Ragan and Sheridan,23 and subsequently Brown, Babcock, Clark, and Livingston24 also emphasized the complex deformational features, so they lumped all of the metasedimentary and metavolcanic rocks together under the name “Vishnu Complex,” the approach continued by Babcock,25 who used the term “Vishnu Metamorphic Complex.”
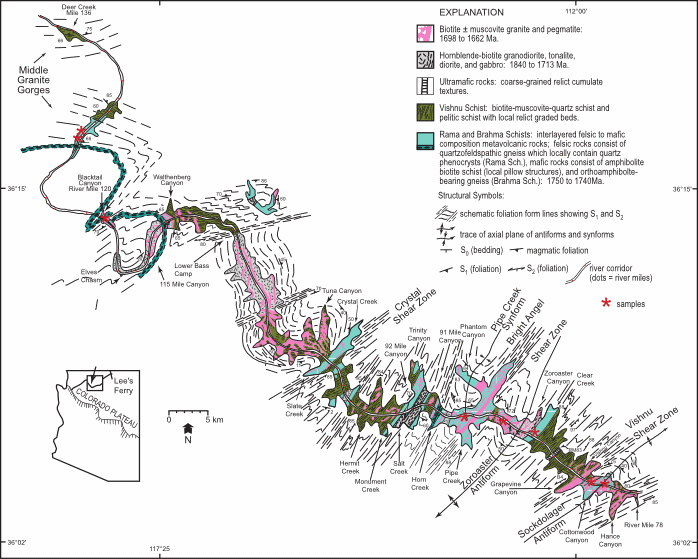
Fig. 1. Simplified geologic map of Paleoproterozoic (lower Proterozoic) rocks in the Upper and Middle Granite Gorges, Grand Canyon, northern Arizona (after Ilg et al.21, Karlstrom et al.22). Form lines outside the Paleoproterozoic exposures show their interpretation of the trace of the regional foliation on the map surface. The transect is divided into metamorphic domains that are generally separated by shear zones. Sample locations are marked.
More recent detailed field mapping, based on the approach that recognizes the need to pursue simultaneously both tectonic and stratigraphic subdivisions of these Lower Proterozoic rocks, has resulted in a new geologic map (fig. 1). Thus, Ilg et al.26 and Karlstrom et al.27 have proposed the new name of Granite Gorge Metamorphic Suite for the entire sequence of metamorphosed volcanic and sedimentary rocks in the Grand Canyon. Furthermore, the new names assigned to the mappable rock units in the Upper and Middle Granite Gorges (fig. 1), as well as the Lower Granite Gorge, are Brahma Schist for the mafic metavolcanic rocks (after the Brahma “series” of Campbell and Maxson28), the Rama Schist for the felsic metavolcanic rocks, and Vishnu Schist for the metamorphosed sedimentary rocks. This designation of only the metamorphosed sedimentary rocks as the Vishnu Schist is probably that which was originally intended by Walcott,29 recommended by Noble and Hunter30 (their Vishnu schist), and proposed by Campbell and Maxson31 (their Vishnu “series”). These metasedimentary and metavolcanic rocks of the Granite Gorge Metamorphic Suite make up about half of the exposed rocks in the Granite Gorges of Grand Canyon, the rest being intrusive rocks (granite, granodiorite, tonalites, and gabbros). Descriptive metamorphic rock names are used for the rocks seen in outcrop and in thin section, and the original sedimentary or volcanic “protoliths” are inferred from rock compositions and a limited number of primary structures that have survived the deposition and metamorphism. Primary structures such as relict pillows and graded bedding show that the original sedimentary rocks were locally deposited on a volcanic sequence, and that the mafic and felsic metavolcanic rocks are commonly interlayered. However, because similar volcanogenic sequences could have been deposited at different times or in separate basins, and such differences would be difficult to unravel due to the subsequent tectonism, this terminology can be considered mainly as lithologic, rather than necessarily stratigraphic.
The Rama Schist consists of quartzofeldspathic schist and gneiss with locally preserved phenocrysts of quartz and feldspar, and possible relict lapilli, that suggest a felsic to intermediate volcanic origin.32, 33 It is dominated by massive fine-grained quartzofeldspathic rocks, but also contains metarhyolites and interlayered micaceous quartzofeldspathic schists and gneisses. The Rama Schist is commonly complexly injected with pegmatite and contains leucocratic layers that may in part reflect preferential partial melting of these rocks due to the peak metamorphic conditions of about 720 °C and 6 kbar.34, 35 It is also locally interlayered with the mafic Brahma Schist.
The Brahma Schist consists of amphibolite, hornblende-biotite-plagioclase schist, biotite plagioclase schist, orthoamphibole-bearing schist and gneiss, and metamorphosed sulfide deposits.36, 37 The petrology and geochemistry of Brahma Schist amphibolites were studied by Clark,38, 39 who divided the amphibolites and mafic schists into five groups based on field occurrence and mineral assemblage: (1) anthophyllite-bearing and cordierite-anthophyllite-bearing rocks (orthoamphibole schist), (2) “early amphibolites,” (3) the Granite Park mafic body (Lower Granite Gorge area), (4) hornblende-bearing dikes, and (5) tremolite-bearing dikes. Ilg et al.40 agreed with Clark’s interpretation that the orthoamphibole-bearing (group 1) rocks are metamorphosed, hydrothermally altered, mafic marine volcanic rocks, and that the “early amphibolites” (group 2) are metamorphosed basalts and basaltic tuffs. Clark’s groups 1 and 2 compose the supracrustal Brahma Schist, following Campbell and Maxson’s original usage of the term.41
Massive amphibolites (part of Clark’s group 2) make up 30–40% of the Brahma Schist. This unit does not typically preserve primary igneous features, but relict pillow structures are present at a number of localities. Massive amphibolites occur in units several meters to tens of meters thick, and are composed of plagioclase and hornblende, plus subordinate quartz, biotite, clinopyroxene, and epidote (plus accessories).42, 43 Furthermore, these massive amphibolites have a tholeiitic character and trace element compositions consistent with an island-arc environment. The biotite-plagioclase and hornblende-biotite-plagioclase schists (the remainder of Clark’s group 2) make up approximately 50% of the Brahma Schist in the Upper Granite Gorge. Although strong tectonic layering has mostly obscured primary igneous textures, in several locations original textures are preserved, such as subangular quartz + plagioclase + biotite fragments entrained in an amphibolitic matrix, which suggests that some of these rocks may have been volcaniclastic breccias. Interlayered with the biotite schists are discontinuous meter-scale lenses of garnet + diopside + epidote + calcite rocks, the protoliths of these lenses possibly being relatively thin layers of calcareous shale or algal mats interbedded with submarine sediments.44 The Brahma Schist also contains exposures of orthoamphibole-bearing rocks (Clark’s group 1) (fig. 1). They are interpreted to be hydrothermally altered, mafic marine volcanic rocks.45 The presence of relict pillow basalt, orthoamphibolite rocks, and associated sulfide mineralization indicates that the Brahma Schist was a product of dominantly mafic submarine volcanism. The Rama and Brahma metavolcanic schists can be complexly interlayered so that contact relationships support variable relative ages between mafic and intermediate metavolcanic rocks. However, in the Upper Granite Gorge, the Rama Schist is underneath and older than the Brahma Schist.
The Vishnu Schist consists of pelitic schist and quartz-biotite-muscovite schists that are interpreted as metamorphosed sandstones and mudstones, with numerous calc-silicate lenses and pods that are interpreted to be concretions.46, 47 Several-kilometer thick sections of meta-lithic-arenite and metagreywacke sequences exhibit rhythmic banded (centimeter-to meter-scale) coarser and finer layers, with locally well-preserved bedding and graded bedding48, 49 suggesting deposition as submarine turbidites. The original grain sizes in the Vishnu Schist metasedimentary rocks probably ranged from medium-grained sand to silt and clay, while conglomerates are conspicuously absent, all of which suggests a lack of high-energy proximal facies. The preserved relict graded bedding, association with metavolcanic rocks containing pillow structures, lack of coarse sediments, and geochemical data50 indicate that these Vishnu metasedimentary units were deposited in submarine conditions on the flanks of eroding oceanic islands (an oceanic island-arc environment). The preserved graded bedding indicates that the Vishnu Schist was deposited stratigraphically above the Brahma Schist, and the accessible exposures indicate that the contact between them is generally concordant, although there is some interlayering of the contact in some places.
These Brahma amphibolites have not previously been dated using radioisotope methods. Metamorphic rocks in general are not easy to date with radioisotopes, because often it is not readily apparent whether the results represent the date of the metamorphic event or the date of the cooling and crystallization of the original rock. However, by U-Pb dating what is believed to be original zircon grains in metamorphosed felsic volcanic units within the Brahma and Rama Schists, it has been proposed that the original basalt lavas were erupted between 1741 and 1750 Ma.51, 52 The subsequent metamorphism of these basalt lavas to form these Brahma amphibolites is believed to have occurred between 1690 and 1710 Ma, based on U-Pb dating of monazite, xenotime, and titanite (sphene) in the overlying Vishnu Schist and underlying Rama Schist, assuming that these minerals formed, or were radioisotopically reset, during the metamorphism.53, 54
Sampling

Fig. 2. Outcropping amphibolites below the Tapeats Sandstone and the Great Unconformity beside the Colorado River, just upstream of Blacktail Canyon (see fig. 1). Seven samples were collected along the river here.
Twenty-seven Brahma Schist amphibolite samples were collected in the Upper and Middle Granite Gorges (with a Scientific Research and Collecting Permit issued by the Grand Canyon National Park): (1) three samples from the Cottonwood Canyon area, (2) nine samples from the Clear Creek area, including seven samples from a single 50 m long and 2 m wide amphibolite body just upstream from the mouth of Clear Creek, (3) one sample from the Cremation Creek area, (4) one sample from near the mouth of Pipe Creek, (5) seven samples from outcrops just upstream of Blacktail Canyon (fig. 2), and (6) six samples from outcrops along the Colorado River between miles 126.5 and 129. All these locations are marked on Fig. 1. The small tabular body of amphibolite near the mouth of Clear Creek was intensively sampled because it appeared to show mineralogical variation through its width, perhaps suggesting that it may have been a thin sill rather than a lava flow (fig. 3). Otherwise, all the other samples were of massive amphibolite. In the area just upstream of Blacktail Canyon, there was clear field evidence that the amphibolites represented a series of basaltic lava flows, there being well-defined competent layers 3–10 meters thick in succession along the outcrop separated by structural breaks accompanied by leaching of the rock (possibly paleoweathering), or in one instance by what appeared to be a thin inter-flow sandstone layer (fig. 4). This sequence of metamorphosed basalt flows was thus systematically sampled.
Chemical and Radioisotope Analyses

Fig. 3. A single amphibolite body (dark rock through the center of the photograph in the erosion gully) that likely represents an original basalt lava flow, just upstream of Clear Creek (see fig. 1). Seven samples were collected from this outcrop and yielded widely divergent K-Ar model ages.
Split by hammering or cutting with a rock saw, a portion of each sample was thin sectioned for subsequent petrographic analysis. Approximately 100 gram splits of each sample were then dispatched to the Amdel laboratory in Adelaide, South Australia, where each sample was crushed and pulverized. Whole-rock analyses were undertaken by total fusion and digestion of each powdered sample followed by ICPOES (inductively coupled plasma-optical emission spectrometry) for major and minor elements, and ICP-MS (inductively coupled plasma-mass spectrometry) for trace and rare earth elements. Separate analyses for Fe as FeO were also undertaken by wet chemistry methods that were able to indicate any sample loss on ignition, primarily as H2O or carbonate (given off as CO2).
A second representative set of 100 gram pieces of each sample was sent to the K-Ar dating laboratory at Activation Laboratories in Ancaster, Ontario, Canada, for whole-rock K-Ar dating under the direction of the laboratory manager, Dr. Yakov Kapusta. After crushing of the whole-rock samples and pulverizing them, the concentrations of K (weight %) were measured by the ICP technique. The 40K concentrations (ppm) were then calculated from the terrestrial isotopic abundance using these measured concentrations of K. The concentrations in ppm of 40Ar*, the supposed radiogenic 40Ar, were derived from isotope dilution measurements with a noble gas mass spectrometer.55, 56

Fig. 4. Outcrop of amphibolite just upstream of Blacktail Canyon (see fig. 1). The vertical layering in the amphibolite appears to parallel the original layering of successive horizontal basalt flows that were subsequently tilted. The rock hammer and brightly colored roll of tape mark the top and bottom of what was an original basalt flow.
Finally, a third representative set of 100 gram pieces of each sample was sent to the PRISE laboratory in the Research School of Earth Sciences at the Australian National University in Canberra, Australia, where under the direction of Dr. Richard Armstrong, whole-rock Rb-Sr, Sm-Nd, and Pb-Pb isotopic analyses were undertaken. After the sample pieces were crushed and pulverized, the powders were dissolved in concentrated hydrofluoric acid, followed by standard chemical separation procedures for each of these radioisotope systems. Once separated, the elements in each radioisotope system were loaded by standard procedures onto metal filaments to be used in the solid source thermal ionization mass spectrometer (TIMS), the stateof- the-art technology in use in this laboratory. Sr isotopes were measured using the mass fractionation correction 86Sr/88Sr = 0.1194, and the 87Sr/86Sr ratios were reported normalized to the NBS standard SRM 987 value of 0.710207. Nd isotopes were corrected for mass fractionation using 146Nd/144Nd = 0.7219 and were normalized to the present-day 143Nd/144Nd value of 0.51268 for standard BCR-1 (a Columbia River basalt, Washington, sample). Pb isotope ratios were normalized to NBS standard SRM 981 for mass fractionation.
Results
The whole-rock major and selected trace element data for all 27 amphibolite samples are listed in Table 1. These analytical results are consistent with these amphibolites being tholeiitic basalts that were metamorphosed without any significant chemical alteration (losses or additions). This can especially be seen in the high MgO, Cr, and Ni contents of the amphibolite in the small body near Clear Creek, which is also high in rare earth elements. Otherwise the range of 43.8%–51.2% SiO2 is typical of the variations found in basalt lavas. Especially noteworthy are the low K2O contents (0.11%–1.96%) of these amphibolites, which are consistent with the absence of any pervasive alteration of the plagioclase in them to sericite, confirmed by petrographic examination (fig. 5). This is particularly relevant to the suitability of these amphibolites for K-Ar radioisotope dating. Any sericitic alteration of the plagioclase would represent post-formation hydrothermal alteration with introduced K2O, so the K2O in these amphibolites is, thus, of the primary in situ origin required for valid K-Ar radioisotope dating. Equally significant are the wide variations in the contents of Rb, Sr, Sm, Nd, U, and Pb in these amphibolites, which make them extremely suitable for radioisotope dating using the isochron method, in spite of the simplicity of their dominant mineralogy (plagioclase + hornblende ± biotite).
The results of the K-Ar radioisotope analyses on these Brahma amphibolite samples are summarized in Table 2. The K-Ar model ages were calculated for each sample analyzed using the standard model-age equation, which assumes that 10.5% of the 40K atoms in each sample decay to 40Ar atoms. Furthermore, because 40Ar is a common atmospheric gas which can leak into rocks and minerals making them appear older than their actual ages, in conventional K-Ar model age determinations it is assumed that a certain proportion of the 40Ar in each rock sample is contamination, and therefore, a certain proportion of the total 40Ar determined in the laboratory on each sample, in accordance with the 40Ar to 36Ar ratio of the present atmosphere, is subtracted so that only what is thus assumed to be the radiogenic 40Ar in each sample is used in the model-age calculations.57 Furthermore, it is convention to assume that no radiogenic 40Ar (written as 40Ar*) was present in the rock when it initially formed, so that all the 40Ar* now measured in the rock has been derived from in situ radioactive decay of 40K. The reported error listed with each model age in Table 2 represents the estimated 1s (sigma) uncertainty due to the analytical equipment and procedure.
Table 1. Major oxide and selected trace element analyses.
| Oxide/ Element | Clear Creek small body | Blacktail Canyon area sequence | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BA-2 | BA-7 | BA-8 | UM-1 | UM-2 | UM-3 | UM-4 | BA-5 | BA-9 | BA-10 | BA-11 | BA-12 | BA-13 | BA-14 | |
| SiO2 (%) | 44.4 | 46.1 | 45.4 | 47.3 | 47.1 | 48.7 | 46.8 | 47.9 | 50.8 | 44.6 | 43.8 | 45.9 | 49.1 | 48.6 |
| TiO2 (%) | 1.05 | 1.00 | 1.09 | 0.68 | 0.78 | 0.62 | 0.47 | 1.03 | 1.13 | 2.30 | 1.21 | 0.70 | 0.80 | 1.06 |
| Al2O3 (%) | 14.4 | 12.9 | 13.9 | 9.53 | 11.0 | 8.29 | 6.00 | 14.5 | 13.4 | 13.2 | 14.4 | 14.8 | 14.6 | 14.9 |
| Fe2O3 (%) | 11.2 | 11.1 | 12.5 | 10.0 | 10.2 | 9.98 | 8.55 | 14.6 | 13.1 | 20.2 | 16.3 | 10.8 | 12.3 | 12.5 |
| MgO (%) | 10.6 | 11.5 | 10.6 | 15.6 | 13.7 | 15.5 | 19.6 | 7.09 | 7.14 | 4.86 | 9.21 | 5.05 | 8.20 | 5.40 |
| MnO (%) | 0.19 | 0.19 | 0.20 | 0.18 | 0.17 | 0.19 | 0.16 | 0.22 | 0.16 | 0.26 | 0.22 | 0.18 | 0.19 | 0.21 |
| CaO (%) | 12.1 | 12.4 | 10.7 | 12.0 | 12.2 | 11.9 | 12.2 | 11.2 | 9.22 | 10.7 | 9.62 | 14.2 | 11.3 | 11.1 |
| Na2O (%) | 0.82 | 0.80 | 0.82 | 0.66 | 0.82 | 0.63 | 0.20 | 2.10 | 3.50 | 2.14 | 1.79 | 2.33 | 2.38 | 2.71 |
| K2O (%) | 1.95 | 1.35 | 1.96 | 1.00 | 0.91 | 1.02 | 0.11 | 0.47 | 0.76 | 0.67 | 1.12 | 1.58 | 0.25 | 1.26 |
| P2O5 (%) | 1.02 | 0.70 | 0.81 | 0.54 | 0.57 | 0.54 | 0.35 | 0.12 | 0.12 | 0.53 | 0.15 | 0.07 | 0.07 | 0.11 |
| LOI (%) | 2.21 | 2.67 | 2.52 | 1.97 | 2.57 | 2.96 | 6.04 | 1.01 | 1.28 | 1.18 | 2.43 | 5.15 | 1.32 | 2.74 |
| Total | 99.94 | 100.71 | 100.50 | 99.46 | 100.02 | 100.33 | 100.48 | 100.24 | 100.61 | 100.64 | 100.25 | 100.76 | 100.51 | 100.59 |
| Cr (ppm) | 320 | 400 | 280 | 900 | 900 | 750 | 850 | 170 | 96 | 78 | 110 | 185 | 210 | 200 |
| V (ppm) | 260 | 240 | 250 | 200 | 210 | 180 | 125 | 290 | 310 | 320 | 320 | 200 | 230 | 310 |
| Ni (ppm) | 99 | 210 | 160 | 440 | 300 | 450 | 700 | 89 | 64 | 62 | 74 | 115 | 120 | 82 |
| Co (ppm) | 57 | 54 | 56 | 60 | 50 | 50 | 60 | 59 | 54 | 54 | 60 | 49 | 49 | 47.5 |
| Cu (ppm) | 49 | 29.5 | 440 | 13.5 | 36 | 115 | 66 | 73 | 84 | 32 | 16 | 96 | 84 | 78 |
| Zn (ppm) | 67 | 84 | 86 | 78 | 80 | 110 | 60 | 105 | 105 | 175 | 150 | 60 | 86 | 100 |
| Rb (ppm) | 91 | 70 | 120 | 58 | 41 | 62 | 1.0 | 8.0 | 15.5 | 11 | 33 | 50 | 2.4 | 35 |
| Sr (ppm) | 430 | 480 | 600 | 200 | 390 | 125 | 140 | 230 | 125 | 100 | 72 | 290 | 200 | 220 |
| Pb (ppm) | 11.5 | 13.5 | 12.0 | 4.5 | 13.0 | 6.5 | 5.5 | 4.0 | 7.0 | 6.5 | 6.5 | 3.0 | 5.0 | 2.0 |
| Th (ppm) | 10.5 | 6.5 | 7.0 | 5.5 | 6.0 | 4.4 | 4.3 | 0.25 | 0.29 | 0.65 | 0.24 | 0.16 | 0.17 | 0.34 |
| U (ppm) | 4.6 | 2.3 | 2.8 | 2.1 | 2.1 | 1.6 | 1.45 | 0.09 | 0.11 | 0.28 | 0.09 | 0.06 | 0.05 | 0.14 |
| Ce (ppm) | 145 | 98 | 105 | 91 | 84 | 66 | 54 | 5.5 | 6.0 | 15.0 | 5.0 | 3.5 | 3.5 | 6.0 |
| La (ppm) | 73 | 52 | 56 | 47.0 | 45.5 | 34 | 29.5 | 2.5 | 2.5 | 7.5 | 2.0 | 1.5 | 1.5 | 3.0 |
| Nd (ppm) | 91 | 100 | 115 | 57 | 88 | 64 | 56 | 5.5 | 8.5 | 21.0 | 8.5 | 5.5 | 6.0 | 8.5 |
| Sm (ppm) | 15.0 | 16.5 | 17.5 | 10.0 | 14.0 | 10.5 | 9.0 | <0.02 | 2.5 | 5.5 | 2.4 | 1.65 | 1.70 | 2.3 |
Table 1b. Major oxide and selected trace element analyses.
| Oxide/ Element | River Miles (RM) 126.5-129 sequence | Cottonwood Canyon | RM 79.85 | Clear Creek area | Cremation Creek | Pipe Creek | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VS-13 | BA-6 | BA-15 | BA-16 | BA-17 | BA-18 | VS-8 | VS-10 | BA-1 | VS-11 | BA-3 | VS-12 | BA-4 | |
| SiO2 (%) | 50.2 | 49.0 | 51.2 | 51.1 | 47.1 | 49.3 | 50.5 | 49.1 | 50.4 | 47.7 | 50.1 | 50.1 | 47.3 |
| TiO2 (%) | 1.31 | 1.95 | 2.33 | 1.12 | 1.14 | 1.75 | 0.99 | 1.11 | 1.20 | 0.79 | 0.92 | 0.76 | 0.49 |
| Al2O3 (%) | 13.2 | 12.7 | 12.3 | 13.1 | 13.7 | 12.2 | 13.8 | 13.0 | 13.6 | 14.7 | 12.6 | 14.7 | 14.0 |
| Fe2O3 (%) | 16.8 | 18.5 | 16.9 | 13.8 | 14.5 | 17.1 | 14.1 | 15.3 | 14.8 | 13.0 | 11.0 | 12.2 | 10.8 |
| MgO (%) | 5.12 | 5.13 | 4.62 | 6.77 | 6.74 | 4.89 | 6.16 | 6.11 | 6.14 | 6.29 | 11.4 | 7.39 | 11.0 |
| MnO (%) | 0.24 | 0.25 | 0.18 | 0.20 | 0.21 | 0.24 | 0.30 | 0.23 | 0.28 | 0.21 | 0.19 | 0.21 | 0.24 |
| CaO (%) | 8.36 | 8.89 | 7.93 | 8.78 | 10.9 | 8.19 | 9.34 | 9.59 | 8.41 | 13.8 | 9.32 | 9.57 | 11.8 |
| Na2O (%) | 3.17 | 2.19 | 2.66 | 3.08 | 2.36 | 2.63 | 2.15 | 1.63 | 1.93 | 0.69 | 0.77 | 2.71 | 2.17 |
| K2O (%) | 0.51 | 0.61 | 0.44 | 0.50 | 0.63 | 0.74 | 1.04 | 1.41 | 1.66 | 0.82 | 1.62 | 1.40 | 1.10 |
| P2O5 (%) | 0.16 | 0.18 | 0.37 | 0.16 | 0.16 | 0.31 | 0.15 | 0.16 | 0.15 | 0.24 | 0.17 | 0.12 | 0.06 |
| LOI (%) | 0.86 | 0.69 | 1.44 | 1.47 | 2.83 | 2.77 | 1.08 | 1.97 | 1.49 | 1.77 | 1.61 | 1.18 | 0.90 |
| Total | 99.93 | 100.09 | 100.37 | 100.08 | 100.27 | 100.12 | 99.61 | 99.61 | 100.06 | 100.01 | 99.70 | 100.34 | 99.86 |
| Cr (ppm) | <2 | <2 | 33 | 165 | 170 | 26 | 63 | 8 | 31 | 130 | 550 | 110 | 480 |
| V (ppm) | 340 | 650 | 390 | 320 | 350 | 380 | 270 | 300 | 330 | 180 | 195 | 230 | 240 |
| Ni (ppm) | 25 | 24 | 28 | 78 | 86 | 28 | 52 | 30 | 37 | 73 | 300 | 69 | 160 |
| Co (ppm) | 49.5 | 66 | 32 | 45.5 | 49.5 | 42 | 46 | 51 | 63 | 39 | 54 | 47.5 | 59 |
| Cu (ppm) | 39.5 | 120 | 150 | 23 | 23.5 | 45.5 | 130 | 43 | 96 | 60 | 6.5 | 48 | 2.0 |
| Zn (ppm) | 145 | 140 | 130 | 115 | 105 | 145 | 250 | 150 | 140 | 87 | 88 | 98 | 175 |
| Rb (ppm) | 11.0 | 8.5 | 4.7 | 9.5 | 16 | 10.5 | 17.5 | 29 | 30 | 22.5 | 82 | 44.5 | 9.0 |
| Sr (ppm) | 220 | 160 | 150 | 165 | 145 | 115 | 360 | 240 | 180 | 320 | 65 | 230 | 210 |
| Pb (ppm) | 5.0 | 5.0 | 8.0 | 5.5 | 3.5 | 6.5 | 34.5 | 11.5 | 8.0 | 10.0 | 6.5 | 6.0 | 6.0 |
| Th (ppm) | 0.81 | 0.92 | 1.10 | 0.29 | 0.37 | 0.63 | 1.0 | 0.63 | 4.1 | 0.24 | 4.9 | 0.87 | 1.95 |
| U (ppm) | 0.35 | 0.39 | 0.51 | 0.13 | 0.17 | 0.24 | 0.64 | 0.45 | 0.40 | 0.29 | 1.35 | 0.36 | 0.26 |
| Ce (ppm) | 13.5 | 15.5 | 18.5 | 5.5 | 8.0 | 14.0 | 11.0 | 16.5 | 18.0 | 11.5 | 43.0 | 9.5 | 5.5 |
| La (ppm) | 7.5 | 8.0 | 9.0 | 2.5 | 4.0 | 7.0 | 6.0 | 9.0 | 9.5 | 8.0 | 23.5 | 5.0 | 3.1 |
| Nd (ppm) | 11.5 | 11.5 | 23.5 | 9.0 | 11.0 | 18.5 | 9.5 | 13.5 | 13.0 | 9.5 | 21.5 | 8.0 | 3.8 |
| Sm (ppm) | 3.3 | 2.4 | 6.0 | 2.6 | 2.8 | 4.8 | 2.6 | 3.3 | 2.9 | 2.4 | 4.6 | 2.2 | <0.02 |
All the results of the Rb-Sr, Sm-Nd, and Pb isotope analyses are listed in Table 3. As expected from the trace element analyses, there is a relatively good spread in the isotope ratios for each of the radioisotope pairs. This is ideal for the plotting of isochrons with good statistics for the fits to the data, and for significant age calculations.
The Isoplot computer program,58 which is now commonly utilized by the geochronology community, was used to process the analytical data for each radioisotope system. This program utilizes the least-squares linear regression method59 to plot the isochron as the best-fit regression line through the data. The slope of the isochron is then used by the program to calculate the isochron age using the standard isochron-age equation. When plotted, each data point has assigned to it error bars that represent the estimated 2s uncertainties due to the analytical equipment and procedure. The program also evaluates the uncertainties associated with the calculated isochron age using a statistic known as the “mean square of weighted deviates” (MSWD), which is roughly a measure of the ratio of the observed scatter of the data points from the best-fit line or isochron to the expected scatter from the assigned errors and error correlations (including, but not limited to, the analytical equipment). If the assigned errors are the only cause of scatter, so that the observed scatter approximates the expected scatter, then the value of the MSWD will tend to be near unity. MSWD values much greater than unity generally indicate either underestimated analytical errors or the presence of non-analytical scatter, while MSWD values much less than unity generally indicate either overestimated analytical errors or unrecognized error-correlations. Thus it is crucial to estimate adequately the analytical errors so that the observed scatter of the data points from the isochron line yields an MSWD near unity. This was the procedure adopted here, so that the isochrons plotted in Figs. 6–8 have MSWDs near unity. The errors for the isochron ages calculated from the isochrons represent the estimated 2s uncertainties. This does not mean that the true age of the samples has a 95% probability of falling within the stated age interval, but rather only signifies that the mean of the infinitely-replicated regressions would yield an isochron age within this interval.
Table 2. K-Ar isotope analyses and “model ages”.
| Location | Sample Code | K2O (wt%) | 40K (ppm) | 40Ar* (nl/g) | 40Ar* (ppm) | 40Ar* (%) | 40Ar*/ Total40Ar | Total 40Ar (ppm) | 40Ar/ 36Ar | 36Ar (ppm) | 40K/ 36Ar | Model Age (Ma) | Uncer- tainty (Ma) (1 sigma) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Clear Creek small body | BA-2 | 1.997 | 1.977 | 93.72 | 0.1671 | 94.03 | 0.9403 | 0.1777 | 4960.3 | 0.0000358 | 55223.5 | 1082.5 | ±29 |
| BA-7 | 1.738 | 1.721 | 79.36 | 0.1415 | 73.3 | 0.733 | 0.1930 | 1108.3 | 0.0001741 | 9885.1 | 1060.4 | ±28 | |
| BA-8 | 1.752 | 1.734 | 95.08 | 0.1695 | 82.1 | 0.821 | 0.2065 | 1650.4 | 0.0001251 | 13860.9 | 1205.3 | ±31 | |
| UM-1 | 1.015 | 1.005 | 87.97 | 0.1569 | 85.85 | 0.8585 | 0.1828 | 2092.5 | 0.0000873 | 11512.0 | 1666.5 | ±63 | |
| UM-2 | 1.011 | 1.001 | 73.58 | 0.1312 | 77.9 | 0.779 | 0.1684 | 1339.0 | 0.0001257 | 7963.4 | 1482.8 | ±39 | |
| UM-3 | 0.776 | 0.768 | 53.92 | 0.0961 | 75.3 | 0.753 | 0.1276 | 1197.7 | 0.0001065 | 7211.3 | 1436.5 | ±38 | |
| UM-4 | 0.118 | 0.117 | 21.34 | 0.0380 | 49.5 | 0.495 | 0.0768 | 585.8 | 0.0001310 | 893.1 | 2574.2 | ±73 | |
| Blacktail Canyon area sequence | BA-5 | 1.474 | 1.459 | 21.95 | 0.0391 | 77.73 | 0.7773 | 0.0503 | 1389.8 | 0.0000361 | 40415.5 | 418.1 | ±12 |
| BA-9 | 0.837 | 0.829 | 42.34 | 0.0755 | 84.7 | 0.847 | 0.0891 | 1933.1 | 0.0000460 | 18021.7 | 1144.3 | ±30 | |
| BA-10 | 0.687 | 0.680 | 45.98 | 0.0820 | 81.5 | 0.815 | 0.1006 | 1598.0 | 0.0000629 | 10810.8 | 1399.7 | ±37 | |
| BA-11 | 0.904 | 0.895 | 49.63 | 0.0885 | 72.2 | 0.722 | 0.1226 | 1065.6 | 0.0001150 | 7782.6 | 1215.8 | ±32 | |
| BA-12 | 1.304 | 1.291 | 41.19 | 0.0734 | 78.4 | 0.784 | 0.0936 | 1372.9 | 0.0000681 | 18957.4 | 794.6 | ±21 | |
| BA-13 | 0.672 | 0.665 | 20.06 | 0.0358 | 58.7 | 0.587 | 0.0610 | 716.8 | 0.0000850 | 7823.5 | 758.6 | ±21 | |
| BA-14 | 1.352 | 1.338 | 38.51 | 0.0687 | 84.6 | 0.846 | 0.0812 | 1925.3 | 0.0000421 | 31781.5 | 730.3 | ±20 | |
| River Miles 126.5–129 sequence | VS-13 | 0.528 | 0.523 | --- | 0.05528 | 53.7 | 0.537 | 0.1029 | 870.5 | 0.0001182 | 4424.70 | 1259 | ±38 |
| BA-6 | 0.607 | 0.601 | 32.80 | 0.0585 | 79.41 | 0.7941 | 0.0737 | 1437.8 | 0.0000512 | 11738.3 | 1201.1 | ±39 | |
| BA-15 | 0.368 | 0.364 | 5.28 | 0.00941 | 74.5 | 0.745 | 0.01263 | 1159.3 | 0.0000108 | 33703.7 | 405.1 | ±10 | |
| BA-16 | 0.653 | 0.646 | 28.42 | 0.0507 | 62.6 | 0.626 | 0.0810 | 791.1 | 0.0001023 | 6314.8 | 1022.2 | ±28 | |
| BA-17 | 0.613 | 0.607 | 24.76 | 0.04414 | 61.1 | 0.61 | 0.0722 | 760.9 | 0.0000948 | 6403.0 | 964.9 | ±26 | |
| BA-18 | 1.323 | 1.310 | 71.82 | 0.1280 | 87.4 | 0.874 | 0.1465 | 2345.8 | 0.0000624 | 20989.9 | 1205.9 | ±31 | |
| Cottonwood Canyon | VS-8 | 1.138 | 1.126 | --- | 0.1440 | 92.3 | 0.923 | 0.1560 | 4571.5 | 0.0000341 | 33020.5 | 1439 | ±37 |
| VS-10 | 0.827 | 0.818 | --- | 0.1147 | 89.5 | 0.895 | 0.1282 | 3507.5 | 0.0000365 | 22411.0 | 1532 | ±39 | |
| RM 79.85 | BA-1 | 2.234 | 2.212 | 109.66 | 0.1955 | 83.4 | 0.834 | 0.2344 | 1783.2 | 0.0001314 | 16834.1 | 1119.4 | ±34 |
| Clear Creek | VS-11 | 0.272 | 0.269 | --- | 0.03036 | 43.2 | 0.432 | 0.07028 | 693.5 | 0.0001013 | 2655.48 | 1318 | ±43 |
| near Clear Creek | BA-3 | 1.527 | 1.512 | 62.51 | 0.1115 | 81.92 | 0.8192 | 0.1361 | 1637.5 | 0.0000831 | 18194.9 | 975.4 | ±24 |
| Cremation Creek | VS-12 | 0.571 | 0.565 | --- | 0.07295 | 73.0 | 0.730 | 0.09993 | 1116.5 | 0.0000894 | 6319.91 | 1447 | ±43 |
| Pipe Creek | BA-4 | 1.138 | 1.126 | 77.98 | 0.1390 | 92.08 | 0.9208 | 0.1510 | 3739.7 | 0.0000403 | 27940.4 | 1372.9 | ±26 |
The K-Ar model ages in Table 2 range from 405.1 ± 10 Ma to 2574.2 ± 73 Ma. The other radioisotope pairs yielded isochron ages of 1240 ± 84 Ma (Rb-Sr), 1655 ± 40 Ma (Sm-Nd), and 1883 ± 53 Ma (Pb-Pb) (figs. 6–8). Unfortunately, the K-Ar isotope data contained too much scatter to yield a statistically viable K-Ar isochron and isochron age. This suggests that a significant component of the data has been perturbed by factors other than simple analytical error. Factors likely to be responsible for the wide variations in the K-Ar model ages include contamination by open-system behavior such as additions from the host wallrocks, and/or perturbing of the K-Ar radioisotope system.

Fig. 5. Representative photo-micrographs of the amphibolite samples collected for this study from outcrops along the Colorado River corridor (see fig. 1). All photo-micrographs are at the same scale (20× or 1 mm = 40mm). The amphibolites are here viewed under crossed polars and consist of hornblende (bright colors, two cleavages) and plagioclase (grey, multiple twinning). There is only occasional minor sericite alteration (speckled, shimmering) of the plagioclase.
- BA-1 (River Mile 78.5)
- VS-11 (Clear Creek area)
- BA-10 (Blacktail Canyon area)
- BA-13 (Blacktail Canyon area)
- BA-6 (River Miles 126.5–129)
- BA-15 (River Miles 126.5–129)
Some of the 27 data points do not plot on the isochrons in Figs. 6–8. The Rb-Sr isochron is defined by only 19 samples, the Sm-Nd isochron by 21 samples, and the Pb-Pb isochron by 20 samples. For each isochron the assigned analytical errors are low and the statistics are excellent.
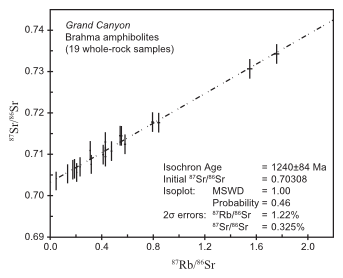
Fig. 6. 87Rb/86Sr versus 87Sr/86Sr isochron diagram for the Brahma amphibolites in Grand Canyon. Nineteen of the 27 whole-rock samples were used in the isochron and age calculations. The bars represent the 2s uncertainties.
The observed scatter matches low assigned analytical errors whenever the MSWD equals unity. The excellent statistics for these isochrons, coupled with the wide spread of the data points, yield isochron ages with low 2s uncertainties. If more data points were included in the Isoplot analyses, both the Sm-Nd and Pb-Pb isochron ages would essentially be the same, but the 2s uncertainties would be higher, whereas the Rb-Sr isochron age would be significantly lower. Only 6–10 samples are routinely used in most radioisotope dating studies for plotting isochrons and calculating isochron ages. The use of 19–21 samples in this study is exceptionally generous. In isochron regression analysis and isochron age calculations outlying data points are frequently excluded in order to improve the isochron fits and the resultant statistics, even when the excluded data plot as close to the isochrons as they do here.
Discussion
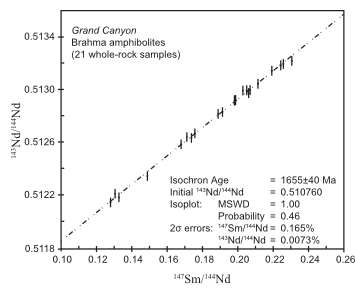
Fig. 7. 147Sm/144Nd versus 143Nd/144Nd isochron diagram for the Brahma amphibolites in Grand Canyon. Twenty-one of the 27 whole-rock samples were used in the isochron and age calculations. The bars represent 2s uncertainties.
These 27 samples of the Brahma amphibolites in Grand Canyon yielded an enormously wide range of K-Ar model “ages,” from 405.1 ± 10 Ma to 2574.2 ± 73 Ma, for a rock unit that is supposed to be 1740–1750 Ma. Even samples only 0.84 meters apart in the same outcrop of the small amphibolite body near Clear Creek (table 2, lower right corner of fig. 1, fig. 3) yielded K-Ar model “ages” of 1205.3 ± 31 Ma and 2574.2 ± 73 Ma. Petrographically these amphibolites are dominated by hornblende which shows no signs of any alteration to chlorite, while the minor plagioclase is not replaced by sericite alteration, which is confirmed by the low whole-rock K2O contents of 0.11–1.96 wt% (table 1). Thus the wide range of K-Ar model ages for these amphibolites cannot be explained by any significant variable alteration. These differences instead could be explained easily by 40Ar* loss from one part of the outcrop and accumulation of excess 40Ar* in the other part of the same outcrop. This could also account for why there is too much scatter in the K-Ar isotope data for this rock unit to produce a viable isochron and a statistically valid isochron age for it. Such an excessively wide range of K-Ar model “ages” and the corresponding inability to obtain a valid K-Ar isochron age, plus the uncertainty over 40Ar* mobility and the role of excess 40Ar*, must cast some doubt over the reliability of K-Ar radioisotope dating. While the Ar-Ar method is now often preferred, due to its ability often to decipher loss or accumulation of Ar, in this study the K-Ar method was used because the Ar-Ar method is usually performed on individual minerals, whereas here the focus was on comparison of the whole-rock analyses of the four major radioisotope systems.
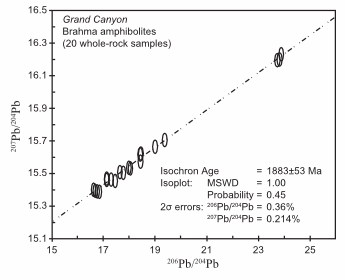
Fig. 8. 206Pb/204Pb versus 207Pb/204Pb isochron diagram for the Brahma amphibolites in Grand Canyon. Twenty of the 27 whole-rock samples were used in the isochron and age calculations. The ellipses represent the 2s uncertainties.
Snelling60, 61 reported much evidence of the mobility of 40Ar* in crustal rocks. This can result in 40Ar* loss from some rock units and some minerals within rock units and 40Ar* excess in other rock units and minerals. As an inert gas which does not chemically bond with the crystal lattices of minerals, 40Ar* can migrate from and through lava flows. Subsequent to their extrusion these lava flows were buried under a considerable thickness of sedimentary and other volcanic strata, and subjected to metamorphism. Thus, there were ample opportunities for 40Ar* to be lost from these rock units to surrounding rock units or the atmosphere. In other rock units excess 40Ar* could accumulate. Even within single rock units there could be regions and minerals whose 40Ar* content has been depleted, and nearby areas and minerals in which excess 40Ar* has accumulated. This explanation might well account for the wide variations in the individual sample K-Ar model ages for the metamorphosed basalts reported in Table 2. Different samples of amphibolite units may contain different quantities of K, and therefore 40K (sometimes vastly different quantities). Nevertheless, all samples from these amphibolites are supposed to be the same age. No matter what their 40K concentrations are, a constant rate of 40K decay should have yielded the same proportional quantities of 40Ar*, so that all samples yielded the same model age. Thus the wide range of K-Ar model ages recorded for these amphibolites must be due to some cause, other than decay rate variability. The mobility of 40Ar* would seem to provide the most likely explanation.
Alternately, it might be postulated that substantial 40K decay has not really occurred but that the 40Ar in the lavas was acquired instead from their mantle source and conduit contacts. However, it is certain that much radioactive decay has occurred throughout the earth’s history, physical evidence for which is provided by radiohalos62, 63, 64, 65 and fission tracks.66 This would thus imply that the K-Ar model ages and Rb-Sr, Sm-Nd, and Pb-Pb isochron ages yielded by these ancient volcanic rocks should be due primarily to radioactive decay of the parent radioisotopes.
Austin67 has discussed the nature of the linear isotope plots for two other rock units. That discussion is equally relevant to the linear isotope plots obtained for the Brahma amphibolites in Figs. 6–8. These isochron plots reveal an extraordinary linearity within the 87Rb-87Sr, 147Sm-143Nd, and 207Pb/206Pb-204Pb radioisotope systems. The extraordinary linearity implies a high degree of statistical consistency undergirding these isochrons and isochron ages, with the isochrons passing within the relatively small estimated range of analytical errors for every one of the data points. As already indicated, the observed scatter in these plots has been fully accounted for by the assigned errors, as measured by the MSWD being at or near unity in each case. By contrast, the attempted isochron plot for 40K-40Ar was not successful because the observed scatter was much too vast to be accounted for, even if the analytical errors were assumed to be much larger than the laboratory estimates.
Snelling68 has reviewed the many problems that beset the major parent-daughter radioisotope pairs. Whole-rock Rb-Sr systems can be disturbed and reset to give good-fit secondary isochrons even by relatively low-grade metamorphism when there may be little field evidence and only relatively minor mineralogical alteration.69 Rb and Sr elemental abundances are known to have been redistributed during metamorphism,70 but such redistribution would not necessarily be systematic, so the Rb-Sr data would not then plot on an isochron as they do for these Grand Canyon Brahma amphibolites. 87Sr loss from hornblende at high temperatures has been documented,71 but in that study the loss was due to contact metamorphism, whereas systematic loss would not be likely during regional metamorphism where the whole region is at a similar temperature, as is evident with the Grand Canyon Brahma amphibolites. Thus, it is not legitimate to discount the reliability of this whole-rock Rb-Sr isochron age of 1240 ± 84 Ma for these amphibolites because it is discordant with the Sm-Nd and Pb-Pb isochron ages for the same rocks, and with the expected age of 1741–1750 Ma for the original basalt lavas based on a zircon U-Pb date for associated felsic lavas.72, 73 After all, the published 10-point whole-rock Rb-Sr isochron age for the Cardenas Basalt in Grand Canyon74 is conventionally regarded as the best constrained radioisotope date for a Grand Canyon rock unit where the Rb-Sr radioisotope system was closed, in contrast to the K-Ar radioisotope system.
On the other hand, great confidence has been placed in Sm-Nd isochron dating of Precambrian igneous and metamorphic rocks because of the belief that the Sm-Nd radioisotope system is not reset, even during highgrade regional metamorphism.75, 76 Although some studies have shown that the Sm-Nd radioisotope system is not remobilized during hydrothermal alteration of felsic rocks, Poitrasson, Pin, and Duthou77 maintain that rare earth element mobility caused by certain hydrothermal conditions does perturb the Sm-Nd system. However, in a study of high-grade metamorphic tonalitic gneisses and mafic rocks, Whitehouse78 showed that the mafic rocks had “retained” the older “true” Sm-Nd age, whereas the Sm-Nd whole-rock radioisotope systems in the non-mafic rocks had been reset to the same age as the U-Pb zircon and other whole-rock radioisotope systems. It has already been noted that there are neither petrographic or geochemical indications in these Grand Canyon Brahma amphibolites of hydrothermal alteration, and being mafic rocks it is thus most likely the Sm-Nd radioisotope system in them has not been reset. Thus this 1655 ± 40 Ma whole-rock Sm-Nd isochron age should be considered as both valid and reliable (in conventional terms). Yet it is discordant with the published accepted ages for the eruption of the original basalt lavas and their subsequent metamorphism, except perhaps that its upper limit does fall within the age range for the metamorphism.
The whole-rock Pb-Pb isochron method is still utilized because it is regarded as reliable, even where U has been mobilized.79, 80 It is argued that if a group of rock samples all have the same age and initial whole-rock Pb isotopic composition, they will then have developed with time different present-day, whole-rock Pb-isotopic compositions according to their respective present-day U-Pb ratios. If the present-day, whole-rock Pb isotopic compositions of a suite of rock samples is then plotted, as has been done here with these Grand Canyon Brahma amphibolites, they are expected to form a straight-line array provided they have remained closed systems, the slope of the array being dependent on the age of the rocks, in this case 1883 ± 53 Ma. However, Pb-Pb isotopic linear arrays are also known to be mixing lines, particularly for mafic volcanic rocks,81 as these amphibolites originally were. Faure admits the problem with a word of caution: “not all linear arrays on the Pb-Pb diagram are isochrons.”82 This Pb-Pb isochron age for these Braham amphibolites is also discordant with the accepted published age based on zircon U-Pb dating of associated felsic volcanic rocks; yet there is no good reason to discard it as unreliable or invalid, because there is no way of determining if this isochron represents a linear array inherited from the original mafic magma source. However, it is more likely that high-grade metamorphism homogenized the whole-rock Pb isotopic compositions but did not reset the Pb-Pb radioisotope system, as with the zircon U-Pb system in the associated felsic volcanic rocks.83, 84 It is often argued that usually zircon U-Pb ages are the best, but they do suffer from the possibilities of the zircons being inherited grains so their U-Pb ages are source ages, and of thermal resetting of the radioisotope systems within them. On the other hand, the whole-rock Pb-Pb system is more likely to have been homogenized but not reset, so it could be argued the whole-rock Pb-Pb isochron age is more reliable.
Therefore, assuming that each of the Rb-Sr, Sm-Nd, and Pb-Pb isochron ages are valid and reliable, it is clearly evident that there is gross disagreement between these radioisotope systems as to the age of these amphibolites. Indeed, the discordances between the isochron ages are pronounced. Snelling et al.85 and Austin86 have discussed explanations for these discordances and have concluded that, since the different radioisotope systems have to be dating the same geologic event, the only explanation that can account for them is that the radioisotope decay rates have not always been constant. Several examples were cited from the geologic literature that similarly report discordant isochron ages for other rock units, most notably for the Great Dyke in Zimbabwe,87, 88 for the Stuart dyke swarm of central Australia,89 and the Uruguayan dike swarm in South America.90 These examples, together with the large number of other examples recorded by Snelling strongly suggest that, where two or more of the commonly-used radioisotope pairs are applied to date rock units, discordances are the norm and not the exception.91
Explanations for these discordances have been attempted.92, 93, 94 For example, different isotope pairs have different closure temperatures that can therefore result in different ages. There may also have been an open-system, magma mixing, inheritance, and/or paleoweathering. It is sometimes suggested that there may have been differing chemical activity of the daughter elements in comparison with the parent elements due to having different chemical properties, which is supposedly why the Pb-Pb age is often the highest. Furthermore, submarine volcanic rocks have been known to retain Ar due to the hydrostatic pressure. Yet while those geologic or geochemical explanations can often seem reasonable, they are not relevant to this study. In nearly every other study reported in the literature, the discordant ages have been obtained by using the different radioisotope methods on different whole-rock samples and/or different minerals. Similarly, in the many studies where concordant ages have been obtained, such as for the Shap Granite in England as reported by Snelling, the different radioisotope methods have been used again both on different samples and different minerals.95 However, in this study all four radioisotope methods were used on the same whole-rock samples. This rules out the possibility of any of these postulated processes having any significant effect on the resultant radioisotope ages. The high-grade metamorphism would have affected all four radioisotope systems similarly. Using whole-rocks for the analyses homogenizes any different chemical or system behaviors in the different minerals. In any case, these amphibolites are essentially just simple, two-mineral systems (fig. 5). Thus, this somewhat uniform approach makes it more likely that the discordances are due to the radioisotope decay rates having not always been constant.
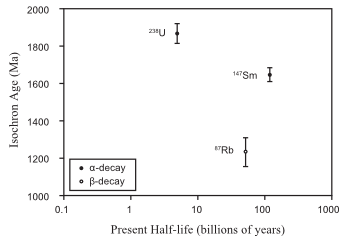
Fig. 9. The isochron ages yielded by three radioisotope systems for the Brahma amphibolites, Grand Canyon, plotted against the present half-lives of the parent radioisotopes according to their mode of decay.
There is a pattern to the isochron discordances. The isochron ages consistently indicate that the a-emitters (238U, 235U, 147Sm) yield older ages than the ß-emitters (87Rb and 40K) when used to date the same geologic event—that is, the formation of a specific rock unit. In the case of the Brahma amphibolites, none of the isochron ages date the eruption of the original basalt lavas at 1740–1750 Ma, the value based on U-Pb concordia dating of zircon grains in metamorphosed felsic volcanic lavas within the associated Brahma and Rama Schists that are believed to have survived the metamorphism without the U-Pb radioisotope system being reset.96, 97 Nor do the isochron ages yield the accepted date for the metamorphism of the original basalt lavas to form the amphibolites. That event has been placed at 1690–1710 Ma, on the basis of U-Pb concordia dating of metamorphic monazite, xenotime and titanite in the overlying Vishnu Schist and underlying Rama Schist.98, 99 Nevertheless, assuming the isochron ages for the Brahma amphibolites are dating the same geologic event, the formation of the amphibolites, a logical explanation of these data is that the radioisotope decay of the various parent isotopes has not always proceeded at the rates described by the present-day decay constants. Thus, the discordances would instead be due to the parent radioisotopes decaying at different rates from present rates, with the decay rates for the different parent isotopes having been accelerated by different amounts. The data are consistent with the possibility that at some time or times in the past a-decay was accelerated more than ß-decay.
The correlation between the present radioactive decay constants for these a- and ß-emitters and the ages they have yielded for the Brahma amphibolites is illustrated in Fig. 9. Austin100 and Snelling101 provide similar isochron age versus half-life and mode of decay diagrams for the radioisotope systems within other rock units. In each of these examples the a-decaying isotopes (238U and 147Sm) yielded older isochron ages than the ß-decaying isotopes (40K and 87Rb). Among the ß-decaying isotopes, 87Rb has the smaller decay constant and thus the longer half-life, yet in the cited rock units it consistently yields the older ages, for example, double the K-Ar isochron age of the Cardenas Basalt.102 On the other hand, even though 147Sm has the smaller decay constant (and thus the longer half-life) of the a-decaying isotopes, it does not always yield the older isochron age. It does for other rock units,103, 104, 105 but not for the Brahma amphibolites (fig. 9). Perhaps the metamorphism of the original basalt lavas may have reset the Sm-Nd radioisotope system in the resulting Brahma amphibolites but not perturbed the U-Pb radioisotope pairs. If this is the case, then it may also be possible that at some time or times in the past the longer half-life a-emitter 147Sm had its decay accelerated more than the other a-emitters 238U and 235U.
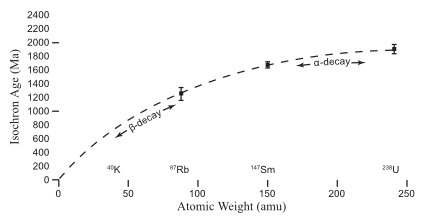
Fig. 10. The isochron ages yielded by three radioisotope systems for the Brahma amphibolites, Grand Canyon, plotted against the atomic weights of the parent radioisotopes according to their mode of decay.
There is another possibility originally suggested by Austin and displayed by Vardiman et al. in their Fig. 5.106 If these isochron ages are plotted against the atomic weights of the parent radioisotopes (fig. 10), there is a clear relationship of increasing isochron age with atomic weight. In this instance, U has a heavier atomic weight than Sm, and the Pb-Pb isochron age is older than the Sm-Nd isochron age. And in this relationship the a-decay ages are older than the one ß-decay (Rb-Sr) age. Whatever mechanism or mechanisms were involved in causing accelerated radioisotope decay, there thus were likely at least three factors involved to produce differing amounts of acceleration for the different parent isotopes—the mode of decay, the present halflife, and the atomic weight. However, with a combination of these three factors influencing the amount of acceleration of the decay rates of the different parent radioisotopes, it might seem that these four methods—K-Ar, Rb-Sr (ß-decay), and Sm-Nd, U-Pb (a-decay)—may not be really enough to resolve the mystery of the mechanism for accelerated decay. Thus, in future studies it is planned to utilize all four ß-decay radioisotope systems—K-Ar, Rb-Sr, Lu-Hf, and Re-Os.
The critical problems with accelerated radioisotope decay have been discussed by Vardiman et al.107 The question of how the heat would have been dissipated is particularly relevant. Volumetric cooling due to concurrent stretching of the fabric of space has been suggested as a viable mechanism.108 Kinnaird has demonstrated that a small change in the binding energies within the nuclei of the parent radioisotopes not only causes the decay rates of the heavier elements to be greatly increased, but drastically decreases the output of heat energy.109 Furthermore, if the accelerated nuclear decay is due to small changes in the forces holding together the nuclei of the parent radioisotopes,110 then the accelerated nuclear decay would not alter the electronic aspects of matter or affect the chemistry of the elements involved. On the other hand, there is clear evidence that there may not have really been a heat problem. Because 238U radiohalos in biotite flakes are annealed at and above 150 °C, if there had been too much heat during accelerated 238U decay, no 238U radiohalos would have formed and still be visible today.111
In any case, it is clear that the different radioisotope systems produced discordant isochron ages for the same geologic event (the eruption of the original basalt lavas or their subsequent metamorphism). For this discordance to be due to changes in radioisotope decay rates, the a-decay rates must have been accelerated more than the ß-decay rates. It is also possible that the longer the half-life of a radioisotope, whether a or ß-emitter, the more its decay has been accelerated at some time or times in the past—that is, the slower the decay rate, the more it is has been temporarily increased. For these reasons, the isochron dating method cannot be relied on to give true real time ages. As with the K-Ar radioisotope system, there are good reasons, many perhaps as yet unknown, for rejecting each of these radioisotope systems as being capable of yielding reliable absolute ages.
Conclusions
The Brahma amphibolites of the Granite Gorge Metamorphic Suite of the Grand Canyon were originally erupted as basalt lavas in a thick sequence of lavas and sediments that suffered high-grade regional metamorphism. This sequence was intruded by granitic plutons to form the crystalline basement of the region. These amphibolites are a very simple whole-rock system, primarily composed of hornblende, with minor subordinate plagioclase. Both petrographic examination and geochemical analyses of the 27 samples used in this study do not suggest these rocks have suffered any significant hydrothermal alteration or regressive metamorphism. The hornblende shows no sign of chloritisation, or the plagioclase of sericitisation, and the K2O contents of the rocks are low.
The samples yielded a wide range of K-Ar model ages, even for adjacent samples from a single outcrop of the same original lava flow. No statistically viable K-Ar isochron age could be calculated because of this scatter in the data. The best and most likely explanation is 40Ar* mobility within these rocks.
The Rb-Sr, Sm-Nd, and Pb-Pb radioisotope systems, on the other hand, yielded good, statistically valid, isochron ages of 1240 ± 84 Ma, 1655 ± 40 Ma, and 1883 ± 53 Ma, respectively. These are clearly discordant with one another, with the published 1741–1750 Ma age for the original basalt lavas (based on zircon U-Pb dating of related felsic volcanics), and with the published 1690–1710 Ma age for the subsequent metamorphism (based on monazite and titanite U-Pb dating of the overlying Vishnu Schist). There are no clear reasons to reject any of these discordant isochron ages as invalid, or not dating the same event. An explanation for this discordancy may be made on the basis of parent radioisotope decay at rates different than presently measured during the interval since these rocks formed. This change in decay rate cannot have been by a single common proportionality factor, applicable to all radioisotope species. Instead, the change in rate must have been different for the different isotope pairs such that the U-Pb system decayed through 1,883 million years (in terms of today’s rate), while the Rb-Sr system decayed through 1,240 million years (likewise in terms of today’s rate) over the identical actual time interval.
The pattern of isochron ages suggests several factors that may have been involved in the acceleration mechanism(s)—mode of decay (a or ß), decay rate, and atomic weight. The a-decaying U and Sm yielded older ages than the ß-decaying Rb, while the heavier atomic weight U yielded an older age than the Sm. In any case, if decay rates have not been constant, radioisotope dating is unreliable and cannot provide valid absolute ages for rocks.
Acknowledgments
Numerous people made this research possible, and all are acknowledged and thanked. The samples were collected with the permission of the National Park Service and the Research Office of the Grand Canyon National Park. Funding for the sampling trips and analytical work was provided by the Institute for Creation Research from donations received towards the RATE project. Help with sampling was provided by Tom Vail, Kurt Wise, and ICR raft tour participants. The reviewers and the editor of the manuscript are thanked for their helpful input that greatly improved the readability of this paper. My wife Kym and my family have tolerated my many long absences on field and other trips, and have supported my research endeavors. Finally, the Lord has faithfully helped and guided to bring research projects like this to fruition.
Footnotes
- Snelling, A. A., 2000a. Geochemical processes in the mantle and crust. In, Vardiman, L., A. A. Snelling, and E. F. Chaffin (eds.), Radioisotopes and the age of the earth: A young-earth creationist initiative, pp. 123–304. El Cajon, California: Institute for Creation Research and St. Joseph, Missouri: Creation Research Society.
- Austin, S. A., 2000. Mineral isochron method applied as a test of the assumptions of radioisotope dating. In, Vardiman, L., A. A. Snelling, and E. F. Chaffin (eds.), Radioisotopes and the age of the earth: A young-earth creationist initiative, pp. 95–121. El Cajon, California: Institute for Creation Research and St. Joseph, Missouri: Creation Research Society.
- Austin, S. A., 2005. Do radioisotope clocks need repair? Testing the assumptions of isochron dating using K-Ar, Rb-Sr, Sm-Nd, and Pb-Pb isotopes. In, Vardiman, L., A. A. Snelling, and E. F. Chaffin (eds.), Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, pp. 325–392. El Cajon, California: Institute for Creation Research and St. Joseph, Missouri: Creation Research Society.
- Austin, S. A., and A. A. Snelling, 1998. Discordant potassium-argon model and isochron “ages” for Cardenas Basalt (Middle Proterozoic) and associated diabase of eastern Grand Canyon, Arizona. In, Walsh, R. E. (ed.), Proceedings of the fourth international conference on creationism, pp. 35–51. Pittsburgh, Pennsylvania: Creation Science Fellowship.
- Snelling, A. A., 2005a. Isochron discordances and the role of inheritance and mixing of radioisotopes in the mantle and crust. In, Vardiman, L., A. A. Snelling, and E. F. Chaffin (eds.), Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, pp. 393–524. El Cajon, California: Institute for Creation Research and St. Joseph, Missouri: Creation Research Society.
- Snelling, A. A., S. A. Austin, and W. A. Hoesch, 2003. Radioisotopes in the diabase sill (Upper Precambrian) at Bass Rapids, Grand Canyon, Arizona: An application and test of the isochron dating method. In, Ivey, R. L., Jr. (ed.), Proceedings of the fifth international conference on creationism, pp. 269–284. Pittsburgh, Pennsylvania: Creation Science Fellowship.
- Austin, Ref. 3.
- Humphreys, D. R., S. A. Austin, J. R. Baumgardner, and A. A. Snelling, 2003a. Helium diffusion rates support accelerated nuclear decay. In, Ivey, R. L., Jr (ed.), Proceedings of the fifth international conference on creationism, pp. 175–195. Pittsburgh, Pennsylvania: Creation Science Fellowship.
- Humphreys, D. R., S. A. Austin, J. R. Baumgardner, and A. A. Snelling, 2003b. Recently measured helium diffusion rate for zircon suggests inconsistency with U-Pb age for Fenton Hill granodiorite. EOS, Transactions of the American Geophysical Union 84(46), Fall Meeting Supplement, Abstract V32C-1047.
- Humphreys, D. R., S. A. Austin, J. R. Baumgardner, and A. A. Snelling, 2004. Helium diffusion age of 6,000 years supports accelerated nuclear decay. Creation Research Society Quarterly 41:1–16.
- Humphreys, D. R., 2005. Young helium diffusion age of zircons supports accelerated decay. In, Vardiman, L., A. A. Snelling, and E. F. Chaffin (eds.), Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, pp. 25–100. El Cajon, California: Institute for Creation Research and St. Joseph, Missouri: Creation Research Society.
- Chaffin, E. F., 2005. Accelerated decay: Theoretical mechanisms. In, Vardiman, L., A. A. Snelling, and E. F. Chaffin (eds.), Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, pp. 525–585. El Cajon, California: Institute for Creation Research and St. Joseph, Missouri: Creation Research Society.
- Karlstrom, K. E., B. R. Ilg, M. L. Williams, D. P. Hawkins, S. A. Bowring, and S. J. Seaman, 2003. Paleoproterozoic rocks of the Granite Gorges. In, Beus, S. S. and M. Morales (eds.), Grand Canyon Geology (2nd ed.) pp. 9–38. New York: Oxford University Press.
- Karlstrom et al., Ref. 13.
- Ilg, B. R., K. E. Karlstrom, D. P. Hawkins, and M. L. Williams, 1996. Tectonic evolution of Paleoproterozoic rocks in the Grand Canyon: Insights into middle-crustal processes. Geological Society of America Bulletin 108(9):1149–1166.
- Powell, J. W., 1876. Exploration of the Colorado River of the west. Washington, D.C.: Smithsonian Institution.
- Walcott, C. D., 1894. Precambrian igneous rocks of the Unkar Terrane, Grand Canyon of the Colorado. US Geological Survey 14th Annual Report for 1892/93, Part 2, pp. 497–519.
- Campbell, I., and J. H. Maxson, 1938. Geological studies of the Archean rocks at Grand Canyon. Carnegie Institution of Washington Year Book 37:359–364.
- Maxson, J. H., 1968. Geologic map of the Bright Angel Quadrangle, Grand Canyon National Park, Arizona, revised. Grand Canyon Natural History Association, Grand Canyon, Arizona, scale 1:48,000.
- Campbell and Maxon, Ref. 18.
- Ilg et al., Ref. 15.
- Karlstrom et al., Ref. 14.
- Ragan, D. N., and M. F. Sheridan, 1970. The Archean rocks of the Grand Canyon, Arizona. Geological Society of America Abstracts with Programs 2(2):132–133.
- Brown, E. H., R. S. Babcock, M. D. Clark, and D. E. Livingston, 1979. Geology of the Precambrian rocks of the Grand Canyon: Part I. Petrology and structure of the Vishnu Complex. Precambrian Research 8:219–241.
- Babcock, R. S., 1990. Precambrian crystalline core. In, Beus, S. S., and M. Morales (eds.), Grand Canyon Geology, pp. 11–28. New York: Oxford University Press & Flagstaff, Arizona: Museum of Northern Arizona Press.
- Ilg et al., Ref. 15.
- Karlstrom et al., Ref. 14.
- Campbell and Maxon, Ref. 18.
- Walcott, Ref. 17.
- Noble, L. F., and J. F. Hunter, 1916. Reconnaissance of the Archean Complex of the Granite Gorge, Grand Canyon, Arizona. U.S. Geological Survey, Professional Paper 98-I:95–113.
- Campbell and Maxon, Ref. 18.
- Ilg et al., Ref. 15.
- Karlstrom et al., Ref. 14.
- Ilg et al., Ref. 15.
- Hawkins, D. P., and S. A. Bowring, 1999. U-Pb monazite, xenotime and titanite geochronological constraints on the prograde to post-peak metamorphic thermal history of Paleoproterozoic migmatites from the Grand Canyon, Arizona. Contributions to Mineralogy and Petrology 134:150–169.
- Ilg et al., Ref. 15.
- Hawkins and Bowring, Ref. 35.
- Clark, M. D., 1978. Amphibolitic rocks from the Precambrian of Grand Canyon: Mineral chemistry and phase petrology. Mineralogical Magazine 42:199–207.
- Clark, M. D., 1979. Geology of the older Precambrian rocks of the Grand Canyon: Part 3. Petrology of mafic schists and amphibolites. Precambrian Research 8:277–302.
- Ilg et a., Ref. 15.
- Campbell and Maxon, Ref. 18.
- Clark, Ref. 38.
- Clark, Ref. 39.
- Babcock, Ref. 25.
- Vallance, T. G., 1967. Mafic rock alteration and isochemical development of some cordierite-anthophyllite rocks. Journal of Petrology 8:84–96.
- Ilg et al., Ref. 15.
- Karlstrom et al., Ref. 14.
- Walcott, Ref. 17.
- Brown et al., Ref. 24.
- Babcock, Ref. 25.
- Hawkins, D. P., S. A. Bowring, B. R. Ilg, K. E. Karlstrom, and M. L. Williams, 1996. U-Pb geochronological constraints on the Paleoproterozoic crustal evolution of the Upper Granite Gorge, Grand Canyon, Arizona. Geological Society of America Bulletin 108(9):1167–1181.
- Ilg et al., Ref. 15.
- Hawkins and Bowing, Ref. 35.
- Hawkins et al., Ref. 51.
- Dalrymple, G. B., and M. A. Lanphere, 1969. Potassium-argon dating: Principles, techniques and applications to geochronology. San Francisco: W. H. Freeman.
- Dickin, A. P., 2005. Radiogenic isotope geology (2nd ed.). Cambridge, England: Cambridge University Press.
- Dalrymple and Lanphere, Ref. 55.
- Ludwig, K. R., 2001. Isoplot/Ex (version 2.49): The geochronological toolkit for Microsoft Excel. University of California Berkeley, Berkeley Geochronology Center, Special Publication No. 1a.
- York, D., 1969. Least squares fitting of a straight line with correlated errors. Earth and Planetary Science Letters 5: 320–324.
- Snelling, A. A., 1998. The cause of anomalous potassium-argon “ages” for recent andesite flows at Mt Ngauruhoe, New Zealand, and the implications for potassium-argon “dating.” In, Walsh, R. E. (ed.), Proceedings of the fourth international conference on creationism, pp. 503–525. Pittsburgh, Pennsylvania: Creation Science Fellowship.
- Snelling, Ref. 1.
- Snelling, A. A., 2000b. Radiohalos. In, Vardiman, L., A. A. Snelling, and E. F. Chaffin (eds.), Radioisotopes and the age of the earth: A young-earth creationist research initiative, pp. 381–486. El Cajon, California: Institute for Creation Research and St. Joseph, Missouri: Creation Research Society.
- Snelling, A. A., 2005b. Radiohalos in granites: Evidence for accelerated nuclear decay. In, Vardiman, L., A. A. Snelling, and E. F. Chaffin (eds.), Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, pp. 101– 207. El Cajon, California: Institute for Creation Research and St. Joseph, Missouri: Creation Research Society.
- Snelling, A. A., and M. H. Armitage, 2003. Radiohalos—a tale of three granitic plutons. In, Ivey, R. L., Jr. (ed.), Proceedings of the fifth international conference on creationism, pp. 243–267. Pittsburgh, Pennsylvania: Creation Science Fellowship.
- Snelling, A. A., J. R. Baumgardner, and L. Vardiman, 2004. Abundant Po radiohalos in Phanerozoic granites and timescale implications for their formation. EOS, Transactions of the American Geophysical Union 84(46), Fall Meeting Supplement, Abstract V32C-1046.
- Snelling, A. A., 2005c. Fission tracks in zircons: Evidence for accelerated nuclear decay. In, Vardiman, L., A. A. Snelling, and E. F. Chaffin (eds.), Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative , pp. 211–326. El Cajon, California: Institute for Creation Research and St. Joseph, Missouri: Creation Research Society.
- Austin, Ref. 3.
- Snelling, Ref. 1.
- Zheng, Y.-F., 1989. Influences of the nature of the initial Rb-Sr system on isochron validity. Chemical Geology 80:1–16.
- Dickin, Ref. 56.
- Hanson, G. N., and P. W. Gast, 1967. Kinetic studies in contact metamorphic zones. Geochimica et Cosmochimica Acta 31: 1119–1153.
- Hawkins, et al., Ref. 51.
- Ilg et al., Ref. 15.
- Larsen, E. E., P. E. Patterson, and F. E. Mutschler, 1994. Lithology, chemistry, age and origin of the Proterozoic Cardenas Basalt, Grand Canyon, Arizona. Precambrian Geology 65:255–276.
- Snelling, Ref. 1.
- Dickin, Ref. 56.
- Poitrasson, F., C. Pin, and J.-L. Duthou, 1995. Hydrothermal remobilization of rare earth elements and its effects on Nd isotopes in rhyolite and granite. Earth and Planetary Science Letters 130:1–11.
- Whitehouse, M. J., 1988. Granulite facies Nd-isotopic homogenization in the Lewisian Complex of northwest Scotland. Nature 331:705–707.
- Snelling, Ref. 1.
- Dickin, Ref. 56.
- Moorbath, S., and H. Welke, 1969. Lead isotope studies on igneous rocks from the Isle of Skye, northwest Scotland. Earth and Planetary Science Letters 5:217–230.
- Faure, G., 1986. Principles of isotope geology (2nd ed.). New York: Wiley.
- Hawkins et al., Ref. 51.
- Ilg et al., Ref. 15.
- Snelling et al., Ref. 6.
- Austin, Ref. 3.
- Musaka, S. B., A. H. Wilson, and R. W. Carlson, 1998. A multielement geochronologic study of the Great Dyke Zimbabwe: Significance of the robust and reset ages. Earth and Planetary Science Letters 164:353–369.
- Oberthür, T., D. W. Davis, T. G. Blenkinsop, and A. Höhndorf, 2002. Precise U-Pb mineral ages, Rb-Sr and Sm-Nd systematics for the Great Dyke, Zimbabwe—constraints on Late Archean events in the Zimbabwe craton and Limpopo belt. Precambrian Research 113:293–305.
- Zhao, J., and M. T. McCulloch, 1993. Sm-Nd mineral isochron ages of Late Proterozoic dyke swarms in Australia: Evidence for two distinctive events of mafic magmatism and crustal extension. Chemical Geology 109:341–354.
- Teixeira, W., P. R. Renne, G. Bossi, N. Campal, and M. S. D’Agrella Filho, 1999. 40Ar-39Ar and Rb-Sr geochronology of the Uruguayan dike swarm, Rio de la Plata, craton and implications for Proterozoic intraplate activity in western Gondwana. Precambrian Research 93:153–180.
- Snelling, Ref. 5.
- Dickin, Ref. 56.
- Faure, Ref. 82.
- Snelling, Ref. 1.
- Snelling, A. A., 2008. Radiohalos in the Shap Granite, Lake District, England: Evidence that removes objections to Flood geology. In, Snelling, A. A. (ed.), Proceedings of the sixth international conference on creationism, pp. 389–405. Pittsburgh, Pennsylvania: Creation Science Fellowship and Dallas, Texas: Institute for Creation Research.
- Hawkins et al., Ref. 51.
- Ilg et al., Ref. 15.
- Hawkins et al., Ref. 51.
- Hawkins and Bowring, Ref. 35.
- Austin, Ref. 3.
- Snelling, Ref. 5.
- Austin and Snelling, Ref. 4.
- Austin, Ref. 3.
- Snelling, Austin, and Hoesch, Ref. 6.
- Snelling, Ref. 5.
- Vardiman, L., S. A. Austin, J. R. Baumgardner, S. W. Boyd, E. F. Chaffin, D. B. DeYoung, D. R. Humphreys, and A. A. Snelling, 2005. Summary of evidence for a young earth from the RATE project. In, Vardiman, L., A. A. Snelling, and E. F. Chaffin (eds.), Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, pp. 735–772. El Cajon, California: Institute for Creation Research and St. Joseph, Missouri: Creation Research Society.
- Vardiman et al., Ref. 106.
- Humphreys, Ref. 11.
- Kinnaird, M. G., 2007. The “heat problem” for accelerated nuclear decay—another look. Creation Research Society Quarterly 44(2):161–164.
- Chaffin, Ref. 12.
- Snelling, Ref. 63.

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- Available Monday–Friday | 9 AM–5 PM ET
- © 2026 Answers in Genesis

