January 2019’s Total Lunar Eclipse and the Flat Earth

The night of Sunday–Monday, January 20–21, 2019, there was a total lunar eclipse visible across the Western Hemisphere. We had planned an eclipse-watching event at Johnson Observatory here at the Creation Museum that night. But concerns about the very cold temperatures and safety at the observatory for our guests prompted us to cancel it. We had much rain on Saturday, followed by several inches of snow overnight. Then after the snow came very frigid temperatures—the temperature fell throughout the day Sunday, and it was in single digits Fahrenheit by the beginning of the eclipse. Consequently, there was much ice and snow around the observatory where we would have watched the eclipse. That wouldn’t have been safe for our guests.

However, the sky was mostly clear much of Sunday and into the night. So, I watched the eclipse from my home. I set up the observatory’s portable 3.5-inch Questar telescope in my driveway to which I attached my digital SLR camera. I made many trips between the inside of my house and the telescope outside. Besides taking photographs of the eclipse, I also watched the eclipse with just my eyes and with binoculars. A lunar eclipse is one of those astronomical events that doesn’t require a telescope.

Of the more than 200 photographs that I took, I was most pleased with this 13-second exposure that I took during totality. It captures something close to what I saw with the naked eye. Total lunar eclipses are rarely so dark as to make the moon disappear. Typically, the moon assumes some shade of red or orange. This color results as the earth’s atmosphere refracts light into the earth umbra, or shadow. Refraction not only bends light, but it also disperses it into various colors. The earth’s atmosphere also scatters light, but it does so differently at different wavelengths, or colors, of light. These two processes, refraction and scattering, combine to produce reddish hues in the earth’s umbra that are different at each lunar eclipse. I would describe most total lunar eclipses that I have seen as pumpkin or copper. This one was a bit odd because of its shade of red and because the color varied across the moon. I struggled to find a good description, but my research partner, Ron Samec, came up with a good one—strawberries and cream.

There have been reports of a meteoroid impact on the moon during the eclipse. From what I’ve seen, the impact showed up on videos and visually as a brief flash of light about the time that the total phase began. Unfortunately, I neither was looking at the moon nor took a photo at the time, so I didn’t see it. Even if I had taken a photo then, the impact likely would not have shown up.

What Causes Eclipses?

Lunar eclipses happen only when the moon is exactly opposite the sun in the sky. Obviously, the moon must be at full phase for this, but a lunar eclipse doesn’t happen every full moon. Why? The moon’s orbit is tilted to our orbit around the sun by about five degrees. Therefore, the full moon usually is too high or too low for the earth’s umbra to fall on it. Only if the moon is near one of its two nodes, the points where its orbit intersects our orbit around the sun, is an eclipse possible. Therefore, there are two requirements for a lunar eclipse:

• The moon must be full.
• The moon must be near a node.

Notice that, like horseshoes and hand grenades, the moon merely must be close to one of its two nodes for an eclipse to happen. There are two periods per year when the line connecting the moon’s nodes point toward the sun and eclipses are possible. These two eclipse seasons are a little more than a month long each and are about six months apart. This year’s second eclipse season is early this summer, when a solar eclipse and a lunar eclipse will happen. However, neither one of these eclipses will be visible from North America.

Lunar Eclipses and Flat Earth

Many ancient societies eventually figured out that eclipses occur only when these two requirements are met. Consequently, many of those societies could anticipate when eclipses were possible, though they couldn’t predict eclipses with much precision. This knowledge made it obvious that the earth’s shadow falling on the moon must be the cause of lunar eclipses. Some of those ancient people also noticed that the earth’s shadow always is a circle. A flat, round earth could cast a circular shadow, but only if the eclipse is at midnight and then only if the moon were high in the sky, as it is during the winter. But if the earth were disk-shaped and an eclipse happened near sunrise or sunset, the earth’s shadow could not be circular. Since the earth’s shadow on the moon always is a circle, some ancient societies concluded that the earth is a sphere. For instance, the earth’s shadow being round was one of the arguments that Aristotle gave for the earth being a sphere (c. 350 BC).

Most of us grew up learning the flat-earth myth, that, until the time of Christopher Columbus five centuries ago, nearly everyone thought that the earth was flat. However, at least in the West, the earth’s spherical shape was established more than two millennia ago. The flat-earth myth was created by skeptics in the nineteenth century as an attack on Christianity and the authority of the Bible. They falsely claimed that the Bible, and therefore the church, had taught that the earth was flat. Neither is the case. Unfortunately, some Christians at the time bought this lie and came to believe that the Bible teaches that the earth is flat. The flat-earth movement faded in the early twentieth century, but recently there has been a resurgence in the flat-earth movement fueled by the internet and social media. Anyone who has read my blogs or some of my other articles at the Answers in Genesis website knows that I have been critical of the current flat-earth movement.

If lunar eclipses are caused by the earth’s shadow, then the circular shape of that shadow is powerful evidence that the earth is a sphere.

If lunar eclipses are caused by the earth’s shadow, then the circular shape of that shadow is powerful evidence that the earth is a sphere. Consequently, flat-earthers strenuously deny that this is what is happening at lunar eclipses. Furthermore, the earth’s shadow can’t fall on the moon in the cosmology of modern flat-earthers. Their cosmology is a disk-shaped earth covered by a dome to which the stars are attached. The sun and moon move around inside that dome. In this model, the sun and moon are perpetually above the earth’s surface. How do flat-earthers explain sunrise and sunset (and moonrise and moonset) in their model? They claim that the sun and moon only appear to rise and set due to perspective. This explanation doesn’t work, but true believers in the flat earth won’t listen to the evidence. How do flat-earthers explain lunar eclipses? They don’t. They merely assert that something else must move between us and the moon during a lunar eclipse. They never get around to identifying what this something else might be. And they probably never will, because none of the flat-earthers I know seem to be the least bit curious about that.

Testing the Cosmology

Some of the photos that I took in the recent lunar eclipse allowed me to test a prediction of the conventional understanding of lunar eclipses. Since the earth is a sphere, its umbra that falls on the moon must be a circle. But how large is that circle? In the figure, let the green circle with diameter D be the earth. The sun subtends an angle, θ, of a little more than ½ degree. Therefore, the earth’s shadow will be a cone having the circumference of the earth as its base and the angle θ at its apex. The figure shows this cone in a sideview cross section as an isosceles triangle. Obviously, since θ is only ½ degree, this figure is not to scale. Let L be the distance between the earth and the apex of its shadow. The length L will be given by

L=D/tanθ

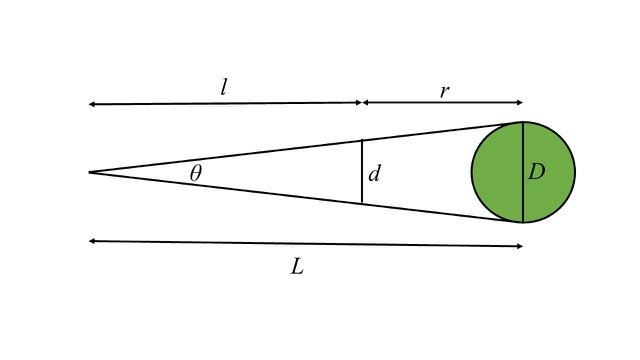
The earth’s diameter is 12,742 km. The angle θ is a little more than ½ degree. However, θ varies throughout the year. What was its value on January 21? I found that value to be 32.5 arcminutes = 0.54 degrees. This yields L being 1.348 x 10⁶ km. Let d be the diameter of the earth’s shadow at the moon’s distance, r, from the earth. Let l be the distance of the moon to the apex of the earth’s shadow. Therefore, l = L – r. Notice that in the diagram, d is the base of a second isosceles triangle that is similar to the first isosceles triangle. Therefore, we can set up the ratio

d/D=l/L

Since the moon’s orbit is elliptical, the moon’s distance from the earth, r, varies. I found that the moon’s distance from the earth at the time of the eclipse was 357,716 km. Therefore, l = 9.901 x 10⁵ km, from which I determined d = 9,360 km. The moon’s diameter is 3,474 km. Therefore, at this eclipse the earth’s umbra was 9,360/3,474 = 2.69 times larger than the moon. This calculation of the earth’s umbra is based on the edge of the earth being sharp. While the surface of the earth is sharp, the earth’s atmosphere tends to change the size of the earth’s umbra slightly and make its edge a bit fuzzy. This uncertainty in the size of the umbra and the fuzziness of its edge results in a few minutes of uncertainty when comparing measured and calculated timings of when the earth’s umbra reaches parts of the moon’s surface. Nevertheless, let me now test this prediction of the size of the earth’s umbra.

The next figure shows two photographs that I took during the partial phases of the lunar eclipse. The photo on the right was prior to totality, and the photo on the left was from after totality. The moon’s monthly motion took the moon right to left (west to east) through that shadow. By eye, I drew a circle to fit the curve of the shadow on the moon. Once I was satisfied with the fit, I printed the image on paper and measured the diameters of the circle and the moon on the paper. The circle was 12.4 cm across, and the moon’s images were 4.3 cm across. This results in a ratio of 2.88. This is a difference from my predicted value of 6.8%.

Considering the uncertainties of either calculation, this is a good match. Therefore, my experimental results confirm the theory that lunar eclipses are caused by the earth’s shadow falling on the moon, as well as the distance of the moon from earth. Lunar eclipses remain the best method that most people can see for themselves that the earth is a sphere. It’s remarkable that flat-earthers don’t have much to say about lunar eclipses. They can’t deny that something happens during a lunar eclipse, but they seem to have no curiosity about what is going on. I find that to be very strange. In an informal internet discussion with some flat-earthers, I found that very few of them even bothered to watch this eclipse. That’s a pity, because it was a beautiful and wonderful thing to see. And the origin of lunar eclipses is a mystery to flat-earthers. Most people are attracted to mysteries because, well, they’re mysterious. But, apparently flat-earthers are not. It’s almost as if they are afraid of the truth.