Celestial Navigation and Flat Earth

What Is Celestial Navigation?

One minor argument that rose in popularity is celestial navigation. One definition of celestial navigation is “the action of finding one’s way by observing the sun, moon, and stars.” Flat-earthers often claim that for thousands of years, people have used celestial navigation to figure out where they are on a flat earth. This is ironic. Many of the best arguments for the earth being spherical come from observing celestial bodies, which flat-earthers usually dismiss by saying, “Why would you look up to the sky to figure out what shape the earth is? That makes about as much sense as looking at the ceiling of a room to figure out what shape the floor is.” Touché. If we cannot infer the earth’s shape by looking at the sky, as flat-earthers claim, then why would flat-earthers look at the sky to figure out where they are on a flat earth? (Note the contradiction!) Flat-earthers seem to be incapable of applying their reasoning to their own arguments.

I think what flat-earthers have in mind about celestial navigation is something akin to determining directions by looking at the sky. For instance, in modern times, Polaris is close to the north celestial pole (less than a degree), so its position in the sky gives a good indication of the direction of north from which the other cardinal directions can be inferred. If one is familiar with the sky as I am, then even if Polaris is not visible, other stars may be used to determine the cardinal directions as well. If one has an intended destination that is in a known direction from one’s starting point, then once one knows the cardinal directions, dead reckoning may be used to find one’s way to the destination. This meaning is consistent with the definition of celestial navigation above. However, that definition of celestial navigation is inadequate. Here is a better definition of celestial navigation: “Use of the observed positions of celestial bodies to determine a navigator’s position.” The navigator’s position is expressed in latitude and longitude. So to fully understand celestial navigation, it is best that we begin with a review of latitude and longitude, which form the foundation of this method.

The Geographic Coordinate System

Flat-earthers don’t seem to be aware that latitude and longitude are coordinates based on a spherical earth.

Flat-earthers don’t seem to be aware that latitude and longitude are coordinates based on a spherical earth. I will describe that system of coordinates, as well as two coordinate systems in the sky. Later, I will attempt to explain what flat-earthers think latitude and longitude are.

The earth spins once per day around an axis. The two points where the axis passes through the surface of the earth are the poles. A great circle is the intersection of a plane with the surface of a sphere, with the plane passing through the center of the sphere (dividing the sphere into two halves). A system of great circles may be drawn through the poles that pass through every point on the earth’s surface. A meridian of longitude is one-half of one of these great circle arcs, extending from pole to pole, so every point on the earth’s surface lies on one and only one meridian of longitude. All meridians of longitude are equivalent, so there is nothing special about any of them. We select one meridian of longitude to be the prime meridian, from which longitudes are measured. By convention, the prime meridian originally was defined as passing through the Royal Observatory in Greenwich, England. The longitude of a location is the angle, expressed at the earth’s center, between the meridian of longitude of the location and the prime meridian. Figure 1 shows the longitude, λ, of a point on the earth’s surface. The prime meridian is to the left, and the point is on a meridian to the right, so the angle, λ, between the two meridians is the longitude. Longitude usually is measured 180 degrees eastward (positive) and 180 degrees westward (negative).

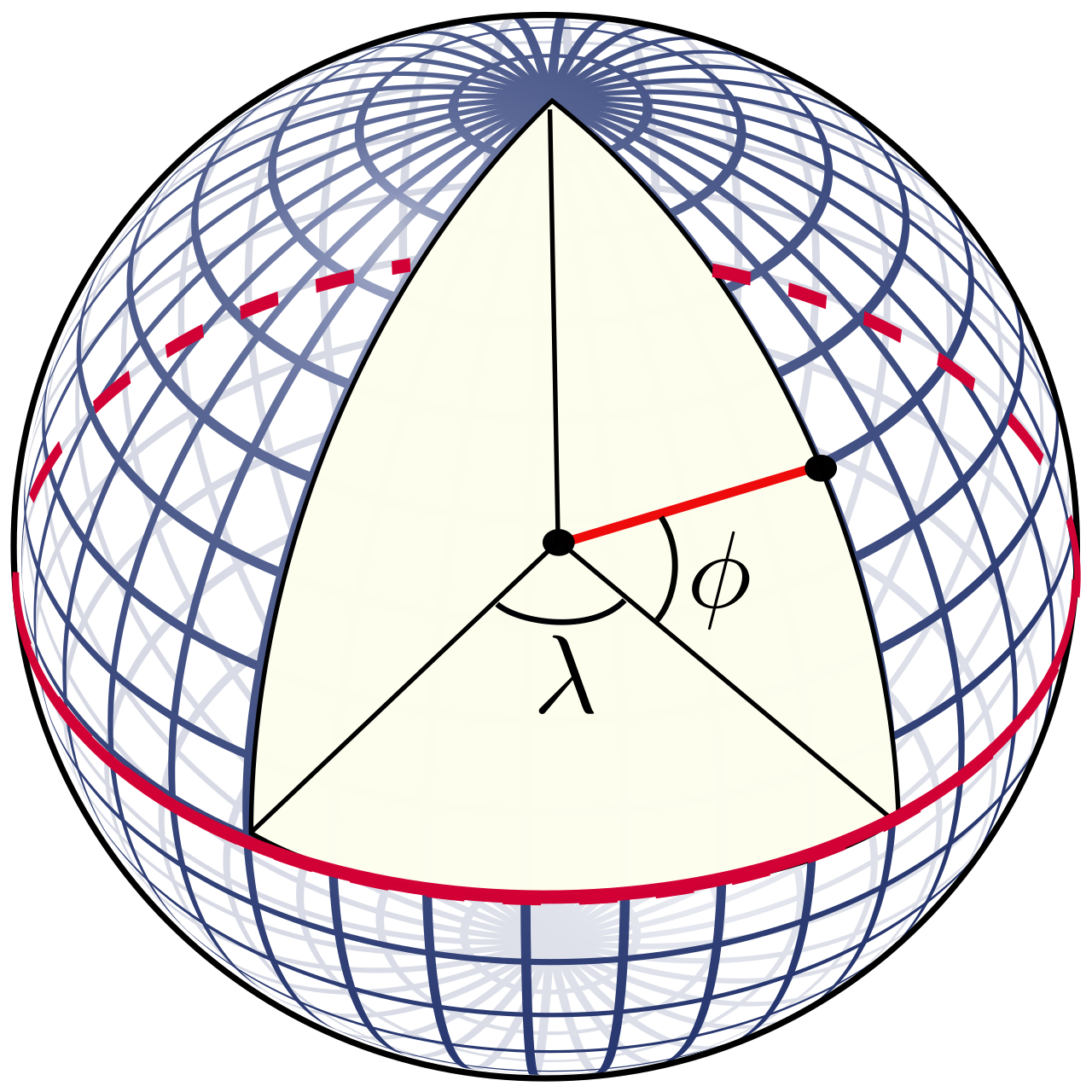
Only one great circle exists perpendicular to the meridians of longitude. It is the equator, located halfway between the poles, dividing the earth’s surface into the Northern Hemisphere and the Southern Hemisphere. To define latitude, we can construct circles in either hemisphere that are parallel to the equator. These are parallels of latitude. Unlike meridians of longitude, parallels of latitude are not equivalent—the equator is the only great circle among the parallels of latitude (all others are smaller circles that decrease in size as they approach the poles), so we use the equator as the reference circle for expressing latitude. The latitude, ϕ, of a location is the angle between the equator and parallel of latitude that the location lies on, expressed from the earth’s center. Latitude is measured from 0 degrees at the equator to 90 degrees northward (in the Northern Hemisphere) and 90 degrees southward (in the Southern Hemisphere).

Note that every location on the earth’s surface has a unique latitude and longitude. Also, note that latitude and longitude are defined as they would be measured at the earth’s center. This is the basis of one of the sillier criticisms some flat-earthers have of celestial navigation, which I will discuss later.

The Equatorial Coordinate System

When one looks up at the night sky, the sky appears hemispherical, as if a dome were over one’s location. However, this is an illusion, for there is no dome over us.1 How does this illusion happen? Using lenses, our eyes and cameras receive light from three dimensions and produce images. These images are two-dimensional, so what we see in images is flat. Our foveal vision (our center of vision) is very narrow, and most camera lenses have only slightly larger fields of view. Consequently, the flat images of our eyes and most cameras are so limited in vista that what we see in these images closely match reality. However, wide-angle camera lenses have much wider fields of view, so the two-dimensional images they produce begin to depart from reality. This shows up as barrel distortion, a common result of wide-angle lenses, causing straight lines to appear curved. This is the classic problem of depicting a curved (three-dimensional) surface onto a flat (two-dimensional) plane. We normally don’t notice the barrel distortion in these lenses, though it is easy to spot in extra-wide-angle lenses, such as fish-eye lenses. I readily see the barrel distortion in the time-lapse videos of stars that I often make with a wide-angle lens—the stars’ motion slightly changes speed and direction as they move across the field of view.

There is a small separation between our eyes, so if objects are close enough, then our two eyes have slightly different images due to a parallax effect. When combining these two images, our brains give us stereoscopic vision, which permits us to judge distances. However, for distant objects, the separation of our eyes is too small to produce noticeable differences in positions in the images our eyes produce, and we lose our stereoscopic vision. For faraway objects that we are familiar with, we can judge their distances by how small they appear to us. This normally works well on the earth’s surface and even for aircraft in the sky. However, this technique fails us when looking at celestial bodies. For instance, sometimes the moon appears in the sky next to a bright planet and a bright star. The star and planet appear as points of light, and the moon appears around half degree in diameter. We have no clues as to the absolute sizes of the three objects, so the moon, planet, and star appear to be the same distance. However, in reality, they’re not even close—the planet can be hundreds or thousands of times farther away than the moon, and the star can be millions of times farther away than the planet. Again, this is due to the image produced by our eyes (and cameras) being flat.

While we do this, we are looking at only a small part of the sky. Our brains tend to interpret what we see in two dimensions, making the sky appear flat, with the plane of the flat image perpendicular to our line of sight. If we turn and face an entirely different direction in the sky, we will interpret what we see there in two dimensions as well, rendering that part of the sky flat as well. Again, the plane of the second two-dimensional image will be perpendicular to our line of sight. Since we are looking in two entirely different directions, the plane we see in the second direction cannot be the same plane that we perceive in the first direction. No matter which direction we look, the sky appears flat locally. That is, the sky appears flat locally while obviously the sky cannot be flat. Our minds automatically perceive these local two-dimensional images at the same distance from us. The definition of a sphere is the locus of all points having the same distance from a central point (the center of the sphere). Therefore, what we see in the sky fits the definition of a sphere, or more technically, a hemisphere, since what we see in the sky is limited to that above the horizon.

If we watch celestial objects for a few hours, we will see many of them rise and set, which easily leads to the conclusion that rather than a hemisphere above us, we are surrounded by a celestial sphere, only half of which can be visible at one time. However, keep in mind that the celestial sphere is an illusion, for the objects on the celestial sphere are varying distances from us. We live in a world with three spatial dimensions, so we need three coordinates to properly locate things. We can define the three coordinates in terms of distance and two coordinates on the surface of a sphere. Keep in mind that unlike the two coordinates on the sphere, we cannot directly observe distance. Consequently, the celestial sphere is a useful device to plot the directions of celestial objects, but not their distances. The ancient Greeks thought that the celestial sphere was not an illusion but that the stars were located on a crystalline sphere. Since the ancient Greeks did not see parallax effects for the stars, the ancients thought that the celestial sphere was very large. For instance, Ptolemy thought that the radius of the celestial sphere was 20,000 times the earth’s radius. This was the dominant Western cosmology for two millennia, abandoned only four centuries ago. But this does not mean that the celestial sphere is not useful. Since the stars are very far away, their positions map as if they were all on a sphere that is very large. Astronomers use this convention. Since the stars appear to map onto a celestial sphere in two dimensions, then we can define celestial coordinate systems on that celestial sphere. Celestial coordinate systems are analogous to latitude and longitude on the earth. There are four such coordinate systems, but only two are relevant to celestial navigation. As with the geographic coordinate system, all spherical coordinates make use of two poles and a great circle perpendicular to the two poles.

One of these celestial coordinate systems is the equatorial coordinate system, illustrated in Figure 2. Since the celestial sphere is concentric with the earth, we can map the geographical coordinate system onto the sky. We can extend the earth’s rotation axis onto the sky to define the north celestial pole and the south celestial pole. We can extend the plane of the earth’s equator onto the sky to define the celestial equator. As the earth spins each day, the sky appears to spin around the two celestial poles, with the greatest apparent speed of objects on the celestial equator. The earth’s orbital plane projects onto the sky as a great circle called the ecliptic. The ecliptic is inclined at an angle of about 23.4 degrees to the celestial equator so that it intersects the celestial equator in two points, the equinoxes. With these references defined, we can define coordinates in the sky that are analogous to latitude and longitude. Similar to latitude, a star’s declination is the angle that the star makes with the celestial equator. Declination extends 90 degrees north of the celestial equator and 90 degrees south of the celestial equator. Rather than saying north or south, declinations are respectively positive or negative. Similar to longitude, we can construct great circle arcs between the celestial poles that are meridians of right ascension. A star’s right ascension is measured eastward from the meridian of the March equinox. Rather than expressing right ascension in degrees as longitude normally is, we usually express right ascension in hours, minutes, and seconds of time. A complete rotation is 360 degrees = 24 hours, so each hour of right ascension spans 15 degrees. The equatorial coordinate system is very useful when using telescopes that are aligned with the earth’s rotation axis. We can point telescopes using target objects’ right ascension and declination. Any telescope at any location on the earth will use the same right ascension and declination for pointing at a particular celestial object.

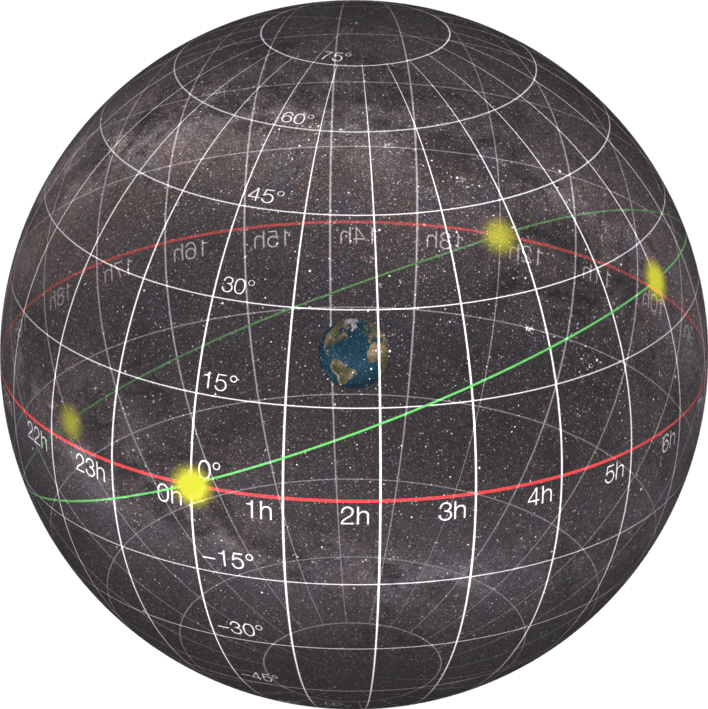
The Horizontal Coordinate System

However, if telescopes at different locations on earth are pointed at the same celestial object, the telescopes will not point in the same direction as defined by their localities. For instance, one telescope may be pointed nearly at the zenith, the highest part of the sky, while another telescope in a very different location may point just above the horizon. This gets to the heart of how celestial navigation works. To see this, we must define a second celestial coordinate system, the horizontal coordinate system. But first, we must define the horizon.

There are at least four definitions of the horizon. The colloquial definition of the horizon (the one that many flat-earthers like to use) is where the sky appears to meet the earth. However, this definition depends upon local topography because hills, buildings, and trees often define where the sky meets the earth. This definition of the horizon would render the horizon useless for celestial navigation because a slight displacement in position could dramatically alter the horizon. The horizon is better defined in an idealized case without local topography. This is not just convenient, but it is also practical because nautical navigation usually is done over the ocean without any local obstructions, and aerial navigation usually is done at high elevation above ground so that it has no local topography either.

The geometric horizon is the point where a tangent line from the observer meets the earth’s surface, assuming an idealized spherical earth and ignoring atmospheric refraction. Since the earth is spherical, the geometric horizon observed from any height above the earth’s surface will be slightly below horizontal (with horizontal defined to be perpendicular to plumb). The astronomical horizon is 90 degrees from the zenith (i.e., a circle perpendicular to the zenith). Hence, the astronomical horizon is horizontal. With any elevation, the geometric horizon will be below the astronomical horizon. This is called dip. Finally, the apparent horizon is where one observes the geometric horizon to be. Due to atmospheric refraction, the apparent horizon often lies beyond the geometric horizon. This usually is accounted for in correcting for dip.

Note that the two coordinate systems that I have described thus far (one on earth and one in the sky) require two poles with a great circle in between the two poles as a reference for one of the coordinates (the other coordinate uses a defined reference meridian). The horizontal coordinate system is illustrated in Figure 3. The horizontal coordinate system uses the astronomical horizon as the reference great circle. The zenith is the highest point in the sky, which is perpendicular to the horizon. The nadir is another point below that is perpendicular to the horizon. The nadir is in the direction of plumb—directly below our feet. The zenith and nadir are the poles through which there are meridians of azimuth. The prime meridian for azimuth is the meridian that intersects the horizon in the north direction. The azimuth of a star is the angle between the north direction and the star’s meridian of azimuth. Azimuth is measured eastward from north (0 degrees) around the horizon up to 360 degrees. Parallels of altitude are circles parallel to the horizon. A star’s altitude is the angle that the star makes with the horizon. Altitude ranges from zero degrees on the horizon to 90 degrees at the zenith. One also can define negative altitudes for objects below the astronomical horizon.

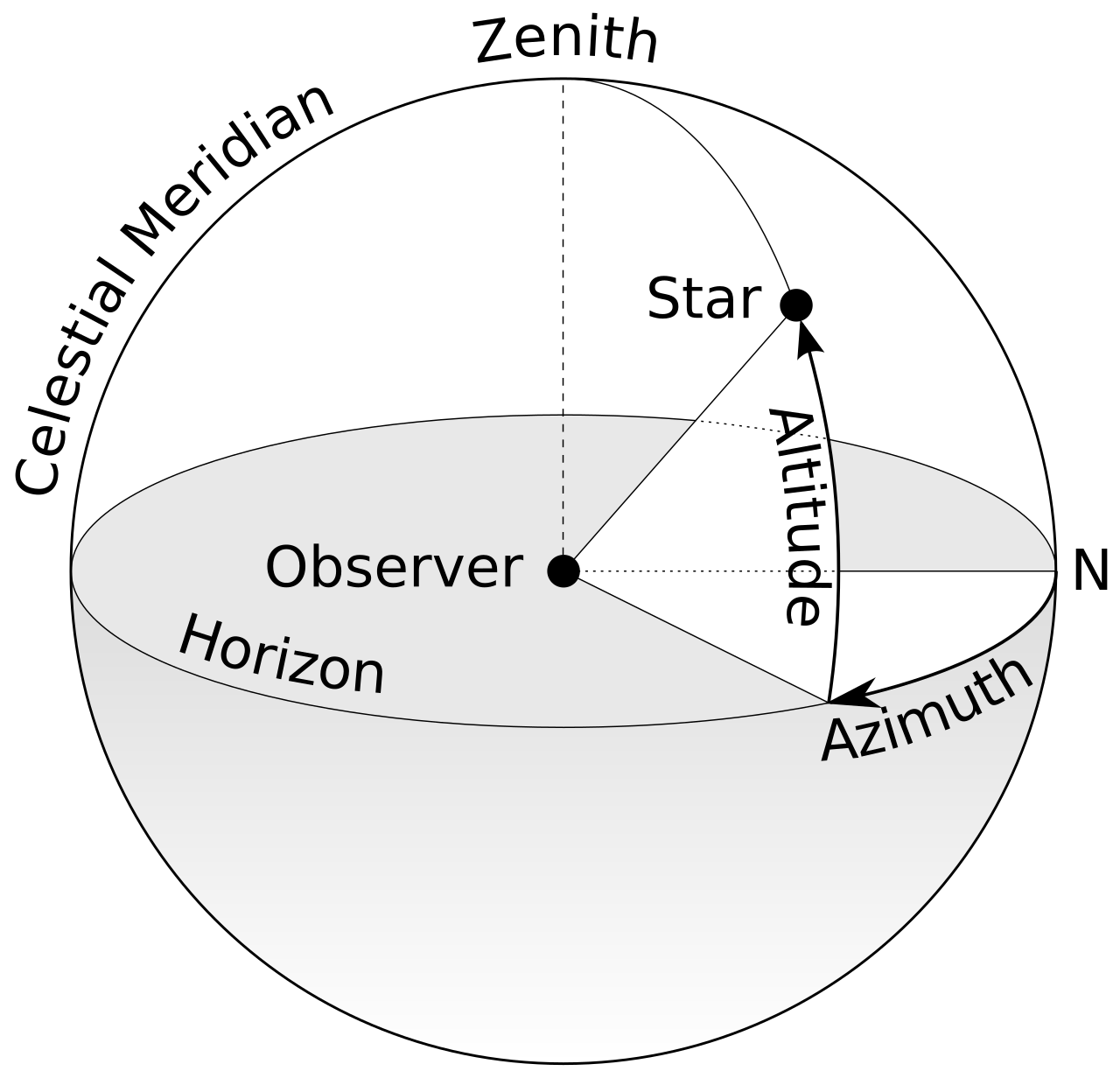
How Celestial Navigation Works

Note that the horizon coordinate system is unique to every location—observers at very different locations looking at the same star will not record the same altitude and azimuth for the star. Even at one location, the altitude and azimuth of the stars will change over time as the earth rotates. That is, the altitude and azimuth of a star will depend on the star’s position on the celestial sphere, the observer’s location on the earth, and the time. Since a star’s position is described by two coordinates in the sky and an observer’s location is described by two coordinates on the earth, the observed altitude and azimuth depends upon five quantities: the right ascension (α) and declination (δ) of the star, the observer’s latitude (ϕ) and longitude (λ), and the time (t). The time standard typically is universal time (UT). There is a very slight difference between UT and Greenwich Mean Time (GMT), but for our purposes, we can consider them to be the same. The right ascension and declination of many stars are tabulated each year in The Astronomical Almanac. Knowing the time, one can use spherical trigonometry to calculate the altitude and azimuth of a star at any time for any location (latitude and longitude) on earth. I have done this procedure many times.

We can reverse this process. One can measure the altitude and azimuth of a star, and knowing the UT, one can use spherical trigonometry to calculate one’s latitude and longitude. The sextant is a device that is used to accurately measure a star’s altitude. One could turn the sextant sideways to measure a star’s azimuth as well, but this would require knowing the direction to the north. This raises a problem—how does one know which way is north? A magnetic compass could be used, but since the geomagnetic poles do not exactly align with the geographical poles, the north-south direction indicated by a compass deviates from true north-south. The amount of this deviation is called the magnetic declination (sorry for using the term declination two different ways). Magnetic declination is known for most locations on earth, but if one is trying to determine one’s location, then one doesn’t know the amount of magnetic declination to correct for. The simplest way around this difficulty is to measure the altitudes of two widely separated stars in the sky. Why measurements of two stars instead of one? Remember that there are two unknowns in this problem: latitude and longitude of the observer. Recall from algebra that a problem in two unknowns requires two equations. The measurement of the altitudes of two stars provides two equations. Knowledge of the time (UT) allows solving for the only remaining unknowns, one’s latitude and longitude.

While the method using spherical trigonometry outlined above can be used, it rarely is used in practice because it can be unwieldy. Therefore, navigators have developed some shortcuts. There are 57 standard navigational stars. These stars are scattered across the entire celestial sphere, always making at least a few of the 57 stars visible worldwide, even if the skies are not entirely clear. At all times, each of the 57 navigational stars is directly overhead at some location on the earth. This location is called the geographical position (GP) of the star. Since the earth is rotating, the GPs of stars are continually changing. Nautical almanacs tabulate the GPs of the 57 navigational stars throughout each day of the year. When a navigator measures the altitude of a star, he knows that his angular separation on the earth’s spherical surface from the star’s GP is equal to the complement of the star’s altitude. To see this, refer to Figure 4. The black circle represents the earth, with its center at point C. The navigator is located at point P. The navigator’s astronomical horizon is the plane tangent to the earth’s surface at Point P, indicated by the yellow line AP. The navigator’s zenith is along the line CZ. The navigator sights a star in the direction of the red line PB and measures the altitude of the star to be the angle APB. The complement of the altitude is angle BPZ. Since the star is very far away from the earth, the direction of the star from the earth’s center is effectively parallel to the line PB, along the line CS. The star will be at the zenith where line CS intersects the earth’s surface. This is the GP of the star, as indicated in the diagram, The line CZ is a transversal crossing the parallel lines PB and CS. Therefore, angle BPZ and angle SCP are equal. The arc length between the GP and P, when expressed in angular measure, is the same as angle SCP, which is equal to BPZ, the complement of the star’s altitude.

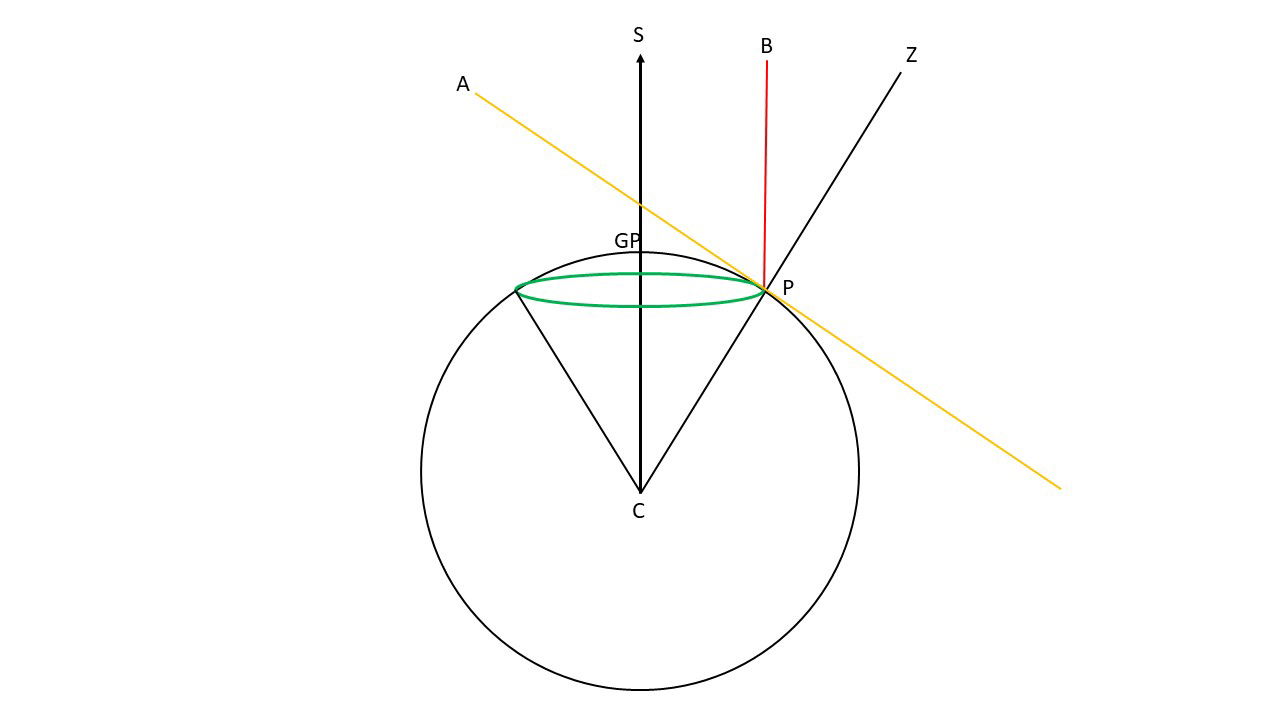
Hence, the navigator knows that his location lies along a circle centered on the GP and has a radius equal to the complement of the star’s altitude (90 degrees minus observed altitude). This circle is shown in green in Figure 4. Navigators use a portion of this circle, called a line of position. Note that a line does not necessarily have to be straight—a line, such as the arc of a circle, can be curved. However, only a small section of an arc, say on a line of position, can be approximated by a straight line. Navigators often draw a small portion of a line of position as a straight line on a navigation chart. Measurement of the altitude of a second star places the navigator on a second line of position. Being circles on the earth’s surface, the two lines of position intersect at only two points. If the navigator has some idea of his location (such as being in the Northern Hemisphere rather than the Southern Hemisphere or roughly knowing his latitude by sighting Polaris), then he can eliminate one of the two points of intersection, and the navigator knows that he is located at the other intersection point. If there is any doubt, then the navigator can measure the altitude of a third star, yielding a third line of position. These three lines of position will intersect at only one point. There are various ways that a navigator can quickly find the intersection of two or three lines of position and hence know his position.

When a navigator measures the altitudes of two stars, he makes two corrections to his altitude measurements before determining his location. The first correction is for dip. Since the navigator is some height above the earth’s spherical surface, he looks slightly downward from the horizontal direction when viewing the apparent horizon. Navigation tables are based on the astronomical horizon (which is horizontal), so the navigator must correct for this dip, using his known height. An additional complication is that atmospheric refraction raises the geometric horizon so the horizon that the navigator sees is a short distance beyond the geometric horizon. The dip correction considers both these effects. The second correction is for atmospheric refraction of the star’s light. Atmospheric refraction causes a star to appear slightly higher in the sky than it geometrically is. The lower in the sky the star is, the greater the amount of refraction. Thus, navigators avoid measuring the altitudes of stars that are very low in the sky. For more information about corrections for dip and atmospheric refraction, see pages 317–319 of Smart (1977). For that matter, chapter 8 (pages 314–339) is an excellent discussion of celestial navigation, which is where I gained most of my knowledge of celestial navigation.

How Flat-Earthers Think Celestial Navigation Works (or Doesn’t Work)

The theory of celestial navigation as I briefly described above is based upon the earth being spherical. For example, tables listing GPs of navigation stars in annual nautical almanacs are prepared assuming that the earth is spherical—not flat. Of course, flat-earthers reject this, but flat-earthers rarely address how on a flat earth GPs of stars are known. An explanation I have heard one flat-earther give is that the “GPs are observationally determined.” Apparently, he thinks that the people who prepare these tables simply have been all over the earth and observed when and where these 57 stars are at the zenith—which is an irrational claim. This begs the question of how these observers knew where they were (latitude and longitude) when they observed the navigation stars to be at the zenith. Furthermore, navigators plot lines of position on maps created assuming that the earth is spherical. Hence, in reality, celestial navigation works only on a spherical earth. On a flat earth, the links between observer altitude, star position, and GP locations would utterly fall apart, thus making navigation impossible. However, flat-earthers are oblivious to this, often simply parroting what other flat-earthers have claimed, blindly asserting that “celestial navigation works only if the earth is flat” (note the absurdity).

I frequently hear flat-earthers repeat talking points about celestial navigation (such as celestial navigation only working on a flat earth), but who is the source of these talking points? The most likely source is John Stunja (aka Quantum Eraser, aka QE), whom I have discussed before. Stunja has discussed celestial navigation many times in his YouTube videos, of which here is one example (I caution the reader that Stunja’s programs often have much profanity and other crude language). Listen for about 10 minutes starting at 47 minutes into this video. Here is another example of one of Stunja’s presentations on celestial navigation, beginning around 1 hour and 41 minutes into the program. Stunja is part of a group of people associated with Nathan Oakley (a staunch flat-earther with a large following). Oakley calls his group “Ballbusters,” a group that I have discussed before. Stunja usually presents his arguments on Oakley’s Discord and YouTube channels. In his daily program, Oakley often repeats many of Stunja’s claims about celestial navigation, and since Oakley is the leader of the group of which Stunja is a part and where Stunja usually presents his material, I shall simply use Oakley’s name as the source for the flat-earther claims about celestial navigation, all the while recognizing that Oakley probably simply summarizes and repeats Stunja’s claims.

First, there is the question of latitude and longitude on a flat earth. In the past, many flat-earthers endorsed an azimuthal equidistant (AE) map with the North Pole at the center or what is known as the Gleason map, shown in Figure 5. Ironically, this is actually a projection of the spherical earth onto a plane with the origin at the North Pole. Such a map is a good representation of the origin, but with increasing distance from the origin, there is much distortion. For instance, in Figure 5, you will notice that Australia is stretched in the east-west direction. Antarctica is “stretched” even more, wrapping all the way around the outer edge of the very large circle, encircling the rest of the earth. An azimuthal equidistant map centered on the South Pole does a good job of accurately depicting the Antarctic and Australia, but the Arctic region, as well as the northern parts of North America and Asia, are greatly stretched. Azimuthal equidistant maps can be generated for any location on earth, not just the poles. They are very useful in navigation because they accurately depict the distances and directions (azimuths) of other locations from the origin of these maps, regardless of how far away those locations are. However, AE maps are not useful for general navigation over long distances.

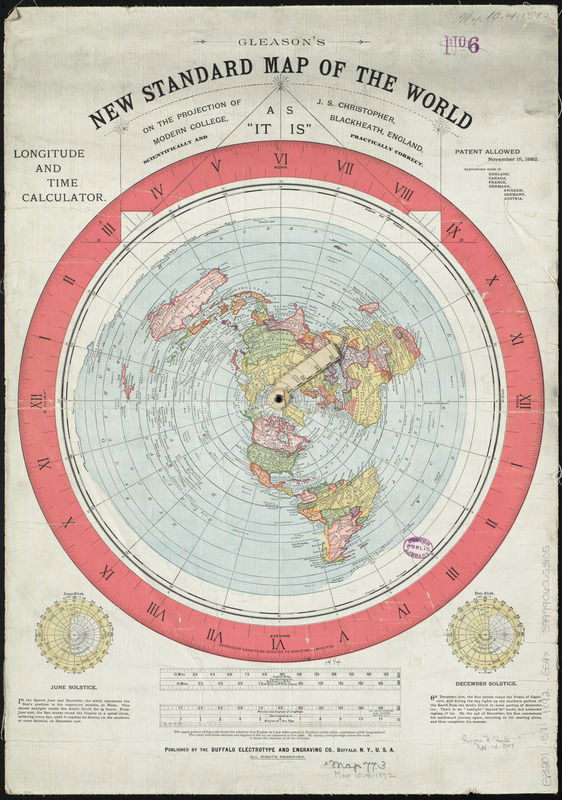
Though flat-earther Alexander Gleason did not invent the azimuth equidistant map, he introduced his azimuthal equidistant map centered on the North Pole in 1892. Flat-earthers in the late nineteenth and early twentieth century apparently liked the Gleason map, thinking that it gave a good representation of the earth. When the flat-earth movement reignited in the second decade of this century, Gleason’s map was widely accepted by flat-earthers. For instance, here is a video by Eric Dubay, a major figure in reintroducing flat earth this century, discussing the Gleason map. Examining any azimuthal equidistant maps centered on the North Pole such as Gleason’s, one can readily see that latitude plots as circles concentric with the North Pole, while longitude lines radiate from the North Pole. The latitudes and longitudes of locations on earth are accurately represented on such a projection, even if distances involving differences in longitude are not. Readers who had a good high school math curriculum should recognize that latitude and longitude on Gleason’s map or similar maps resemble a polar coordinate system.

As popular as the Gleason map has been with flat-earthers, it recently has lost favor with many flat-earthers. Early in 2024, Will Duffy announced an expedition to Antarctica in December 2024 that he called the Final Experiment (TFE). Flat-earthers generally believe that the earth is flat with the North Pole at its center (note that this is basically the Gleason map). Per the typical flat-earth AE map, the sun circles daily above the earth around an axis passing through the North Pole. Throughout the year, the radius of the sun’s daily motion changes, reaching its smallest size on the June solstice, when the sun passes over the Tropic of Cancer, and reaching its greatest size on the December solstice, when the sun passes over the Tropic of Capricorn. This model can explain why there is a 24-hour sun in the Arctic in June, but it cannot explain why there is a 24-hour sun in the Antarctic in December. There have been time-lapse videos of a 24-hour sun in the Antarctic, but flat-earthers generally dismissed those as “fake.” In TFE, Duffy invited several prominent flat-earthers to join him (at Duffy’s expense) at Union Glacier, at 80 degrees south latitude in the Antarctic, in December 2024 to see whether there is a 24-hour sun. A small group of flat-earthers (not all funded by Duffy) and globe-earthers made the trip, and on the trip, all participants agreed that they confirmed that the sun was up continuously over 24 hours. This has prompted some flat-earthers to abandon the belief that the earth is flat, but most flat-earthers dug deeper into their belief. As a result, many flat-earthers have distanced themselves from the Gleason map. Rob Webb and I interviewed Will before and after TFE.

If the Gleason map (or a similar map) does not accurately represent the flat earth, then what are latitude and longitude on the flat earth? I doubt many flat-earthers have pondered this question, though many of them apparently still believe that latitude and longitude can be delineated on a flat earth, with no rational justification for that belief. Oakley has an “answer,” at least for latitude. Oakley says that latitude is equal to the altitude (elevation angle) of Polaris. This is basically correct, but there are two problems. First, this is based upon the belief common among flat-earthers that Polaris is exactly at the north celestial pole, the center of the observed rotation of the stars in the sky. It isn’t, as I’ve already explained. Polaris is currently about 0.7 degrees from the north celestial pole (due to axial precession, this distance will continue to shrink). Consequently, if one were to follow Oakley’s method to measure one’s latitude today, it would vary about 0.7 degrees around one’s true latitude. The latitude measured this way would vary according to the time of night and the date, though the observer stayed at the same location and hence did not change latitude. Polaris usually is included with the 57 navigation stars in nautical almanacs but in a special category. Measuring the altitude of Polaris with a sextant can permit a navigator to roughly determine his latitude (within less than a degree), but Polaris is useless for longitude determinations. So while flat-earthers generally say that latitude can be estimated using Polaris, they utterly lack an explanation for longitude.

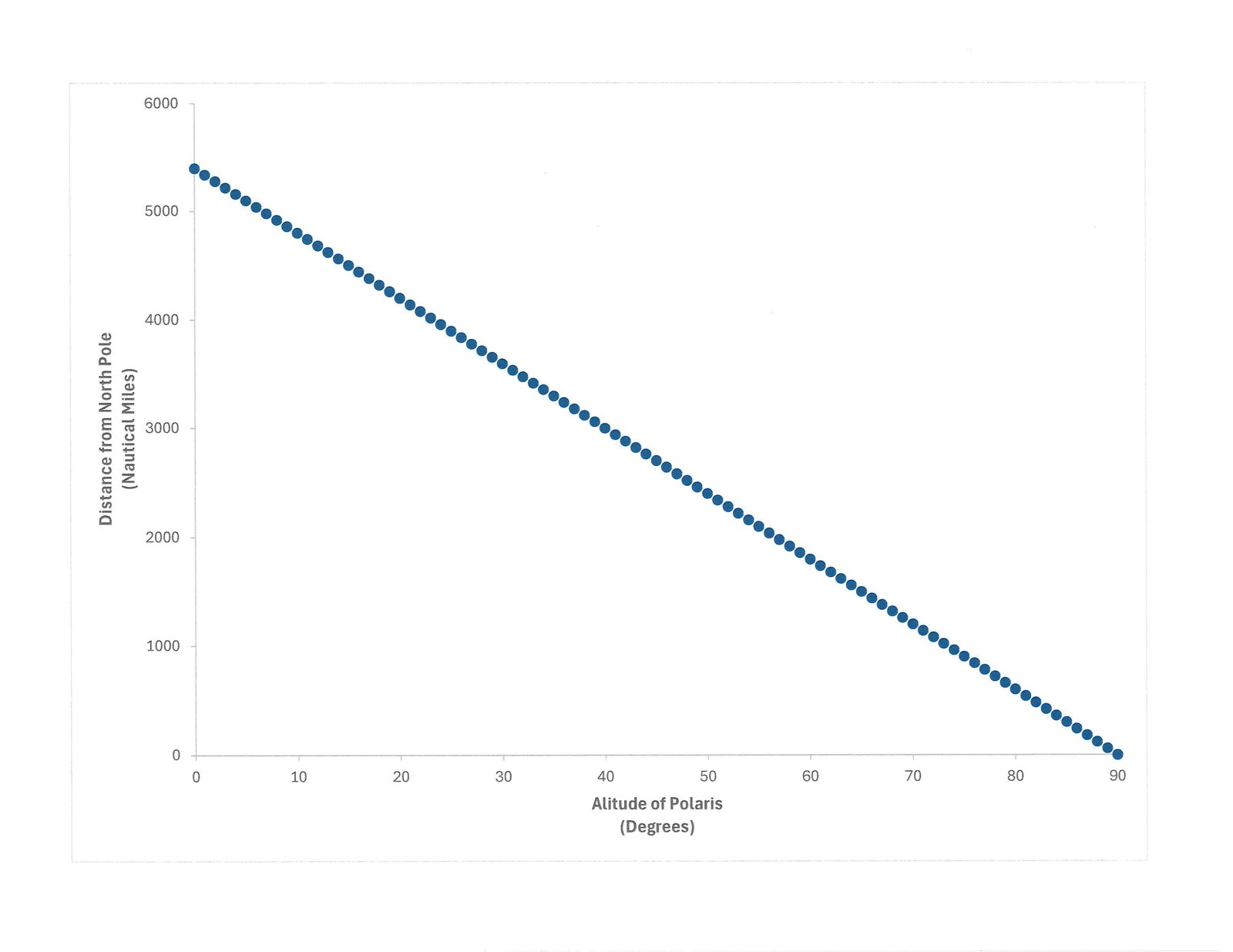
However, an even bigger problem with Oakley’s method of defining latitude is that even if Polaris coincided with the north celestial pole, this would work only if the earth were spherical. It fails on a flat earth. To simplify in demonstrating this, let us lay aside the problem of Polaris not coinciding exactly with the north celestial pole and assume that Polaris is at the north celestial pole. With a spherical earth, what would happen if we defined latitude to be the altitude of Polaris as Oakley thinks latitude is defined? Look at Figure 4 once again. Let the star being observed be Polaris. If the observer is at Polaris’ GP, then the altitude of Polaris is 90 degrees, the latitude is 90 degrees, and the observer is at the North Pole. Suppose that the observer moves away from the North Pole. As the observer departs from the North Pole, the altitude of Polaris will decrease. The altitude of Polaris will decrease approximately linearly as the distance traveled from the North Pole increases. More specifically, for every 60 nautical miles (69 statute miles) traveled south, the altitude of Polaris will decrease one degree. When one reaches the equator (latitude zero degrees), the altitude of Polaris will be zero degrees. This relationship is shown in Figure 6. South of the equator, Polaris will be below the horizon (negative altitude) and hence not be visible. The result is that latitude lines are evenly spaced on the earth, each degree being 60 nautical miles apart.

What is the expectation on a flat earth? On a flat earth, Polaris is some height above the North Pole. Let h be the height of Polaris above the plane of the earth, and d be the distance of the observer from the North Pole. Using very basic trigonometry, the altitude of Polaris, and hence the latitude, ϕ, would be given by

Or rearranging,

Suppose that a person is located at the North Pole, directly beneath Polaris. The altitude of Polaris would be 90 degrees, but the tangent of 90 degrees is undefined. That is because as the angle approaches 90 degrees, the tangent of the angle increases without bound (in colloquial language, people might say that the tangent of 90 degrees approaches infinity). Mathematically, this would result in d being zero, which is the expected value for d, since d was defined as being the distance one is from the North Pole, which is the only place where Polaris is at the zenith.

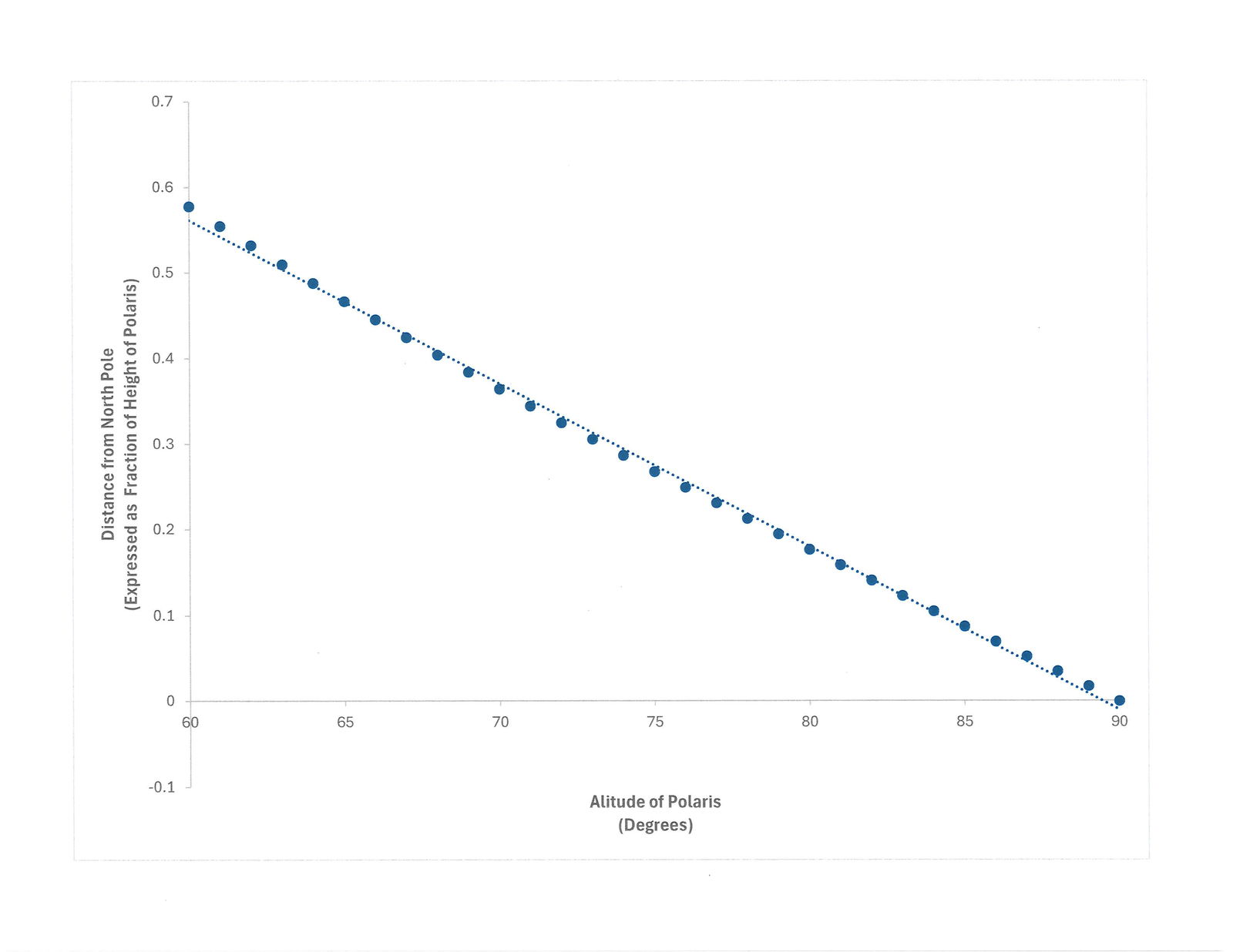
So far, so good. But what happens as the distance, d, increases? Obviously, as one gets farther from the North Pole, the altitude of Polaris must decrease. The above equations describe how the altitude of Polaris must change with increasing distance from the North Pole if the earth is flat. Figure 7 shows a plot of the distance from the North Pole for altitudes between 90 degrees and 60 degrees according to this function. The distance, d, is in terms of the height, h. The points look like they are linear, but they are not, as indicated by the dotted straight line drawn through the points. The points near 60 degrees and 90 degrees lie slightly above the straight line, but the points in the middle, near 75 degrees, lie slightly below the straight line. This indicates that the distance from the North Pole is not a linear function of the altitude of Polaris but rather there is an increase in the rate at which distance changes with decreasing altitude. This is because the tangent function is not linear—it has a hyperbolic nature. If Oakley were correct (he’s not) about how latitude is measured on earth, the latitude lines on earth must get progressively farther apart with increasing distance from the North Pole—which obviously does not match reality.

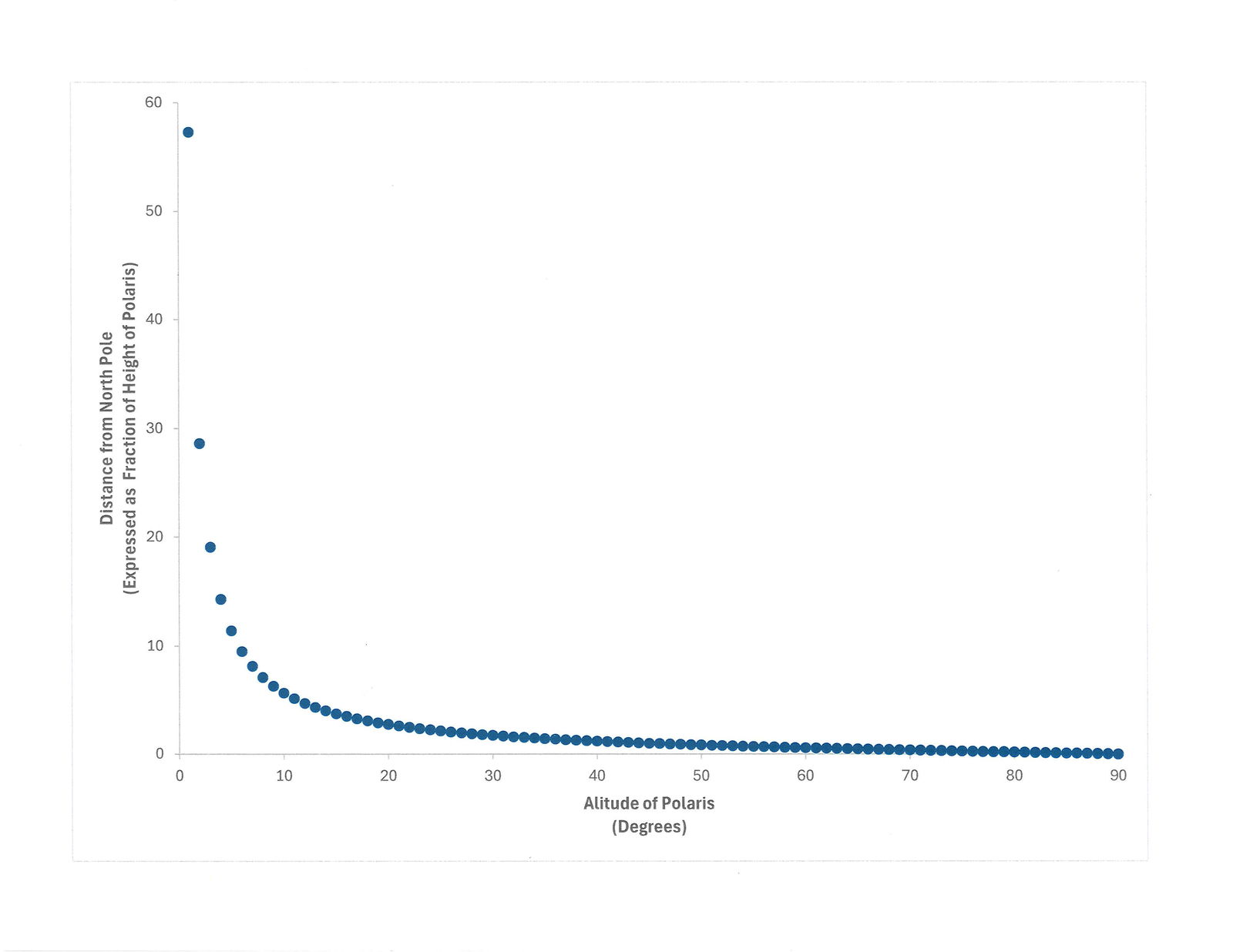
How large does this departure become? Figure 8 shows the distance, d, in the range of altitude between 1 and 90 degrees. The scale of the vertical axis has been changed from Figure 7 to show the departure from linearity. On this scale, the plot is approximately linear until about 20 degrees altitude. At lower altitudes, the distance, d, greatly increases. At one degree latitude north, the distance from the North Pole must be 57 times the height of Polaris above the flat earth. Does any flat-earther believe this to be the distance from the North Pole at a location one degree north latitude? Probably not, but this must be the case if Oakley is correct about how latitudes are measured on a flat earth, thus making their so-called “model” even more implausible. On the earth’s equator, Polaris between upper and lower culmination has zero degrees altitude (corrected for atmospheric refraction). I did not plot zero degrees latitude because the functions above would be undefined, indicating that for one to see Polaris on the horizon on a flat earth, one would have to be infinitely far away from the North Pole. I know that no flat-earther would accept this, for they don’t believe the earth is that large. Note that if Oakley is correct, then as one approaches the equator, parallels of latitude are spaced farther and farther apart. I suspect that few, if any, flat-earthers are aware of this fact.

Compare the predictions of the spherical earth and the flat earth for this definition of latitude, or alternately, a simplified method of measuring latitude. On a spherical earth, latitude lines are evenly spaced, but on a flat earth, latitude lines get progressively farther apart, becoming infinitely far apart on the equator. Which one better represents reality? (The answer is clear!)

Earlier I mentioned a particularly silly flat-earther objection to latitude measurements. Oakley has often criticized the definition of latitude on a spherical earth by pointing out that the angles defining latitude are considered at the earth’s center. From this, Oakley incorrectly reasons that the only way to measure latitude is from the earth’s center, which, of course, would be impossible. Oakley often derisively refers to this as “measuring latitudes in hell.” I must question whether Oakley is serious about this criticism. To call this sophomoric would be insulting to sophomores everywhere. I learned about latitude and longitude in the fourth grade. I am sure that when I was in fourth grade my classmates would have found Nathan’s criticism of the definition of latitude silly. The definition of latitude does not require that latitudes be measured only at the earth’s center. Meanwhile, as I have already demonstrated, Oakley’s claim of how latitude is determined (defined?) is untenable.

Oakley (erroneously) claims that measuring the altitude of stars with a sextant is possible only on a flat earth. Oakley’s reasoning is that an angle is defined to be the relationship between two intersecting straight lines. The direction to the star is a straight line, but if the earth is a sphere, then the other line is not straight but instead is a curve. According to Oakley, this violates the definition of an angle. Ergo, sextants cannot measure angles on a spherical earth, and sextant measurements are possible only on a flat earth. Apparently, Oakley does not understand that a tangent is a straight line that intersects a circle or sphere at one point. The astronomical horizon is defined as the plane tangent to a spherical surface, and hence a tangent line exists in every direction along the astronomical horizon. It does not matter if the earth’s surface is curved because sextant measurements are reduced to the astronomical horizon. It does not matter if the light from the observed horizon takes a slightly curved path to reach the navigator—the perceived direction is a straight line, and hence the navigator makes his measurements along two straight lines. Oakley takes descriptions of altitude measurements from reputable sources and then proceeds to misconstrue what they mean. Coincidentally, as I was writing this, I had Oakley’s daily live program on in the background, and he briefly discussed this topic. To hear what Oakley said about this, you can listen for a minute or two starting around 0:10:20 or for less than a minute around 1:13:15.

Once sextant measurements are completed, how does Oakley think a navigator determines his position? Oakley appeals to the standard answer—that the navigator finds the GPs of the stars measured and determines his position at the intersection of the lines of positions. Of course, Oakley insists that this is possible only on a flat earth. Which flat-earth maps does Oakley propose that we use? When pressed to discuss the specifics of flat earth, Oakley often bellows that “we don’t have a flat-earth map!” If there is no flat-earth map, then how can one determine one’s position on a flat earth using celestial navigation? Without an actual flat-earth map, there is no framework for even plotting GPs or lines of positions—and yet, ironically, they rely on a celestial navigation system designed for a spherical earth. Obviously, Oakley hasn’t thought this through very much, suggesting that Oakley really hasn’t considered the implications of his erroneous and incoherent claims.

Conclusion

Celestial navigation is a very useful purpose for the heavenly bodies that God made on day four (Genesis 1:14–19).

Celestial navigation is a very useful purpose for the heavenly bodies that God made on day four (Genesis 1:14–19). While celestial navigation is not explicitly mentioned among the list of purposes of the heavenly bodies in Genesis 1:14, elements of celestial navigation (“seasons, days, and years”) are mentioned. Thus, we can be assured that celestial navigation is one of the many things that man in his God-given ingenuity can employ in a God-honoring way, even if men do not always recognize this. By using the positions of stars to navigate and explore the earth, we exercise our dominion mandate over creation (Genesis 1:28). Anyone who truly understands how celestial navigation is done cannot possibly think that celestial navigation could work as it does if the earth were flat. Flat-earthers have been deceived into believing a lie when they say that celestial navigation only works on a flat earth. It is sad that some professing Christians have unknowingly fallen into the deception that the earth is flat and repeat the lie—as it contradicts both Scripture and observable reality.