Helium in the Earth’s Atmosphere
Originally published in Journal of Creation 8, no 2 (August 1994): 142-147.
Synopsis
Creationists have used the argument that the amount of helium in the earth’s atmosphere indicates a young earth. It was first brought to the public’s attention by Nobel Prize nominee Melvin A. Cook in 1957, when an article was printed in Nature.1 The rate at which helium is entering the atmosphere from radioactive decay is known fairly well; as is the rate at which helium is presently escaping from the atmosphere into interplanetary space.
However, the Australian Skeptics, in their publication Creationism, an Australian Perspective, have printed an article by Ken Smith, suggesting that creationists have not done their homework properly, and are in fact seriously in error with this conclusion.2 This paper is submitted with the aim of correcting the false claims put forward in the Skeptics’ publication. Much of Ken Smith’s article is highly misleading if not simply wrong as we will here attempt to show.
We will explain how the rate of loss of helium from the atmosphere has been obtained. Since the rate of loss is less than the rate at which helium is entering the atmosphere, the evidence does indicate a young age for the earth (of the order of two million years), a result which is well known amongst atmospheric scientists.
Jeans Escape
To understand the mechanism by which helium is known to be escaping from the atmosphere, we can do no better than quote from the reference Walker.3 In fact we will be relying heavily on this source, as he presents a full and fair treatment of the matter.
Ken Smith accuses creationists of relying on obsolete work done before the International Geophysical Year of 1957–58. However, Walker’s book was written in 1977, so both he and almost all his authorities come after 1958.
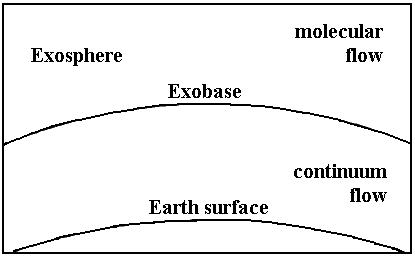
With reference to figure 1, the mechanism of Jeans escape is as follows:
“Let us assume that there is a level in the atmosphere, called the critical level or exobase, above which collisions between molecules are so infrequent as to be negligible and below which collisions are sufficiently frequent to maintain a completely isotropic and random distribution of molecular velocities. At or below the exobase, therefore, the velocity distribution of the molecules of a given atmospheric constituent is the Maxwellian distribution. Since collisions are negligible above the exobase, the molecules in this region, called the exosphere, move along ballistic trajectories under the action of the earth’s gravitational field. Some of the upward-moving molecules have velocities sufficiently great to carry them on hyperbolic trajectories away from the earth, into space.”4
The escape velocity can be found from a known formula.5 At the planetary surface the escape velocity is given by —
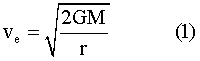
where G is the universal gravitational constant; and r and M are respectively the radius and mass of the planet.
At an altitude Z, the escape velocity6 will be —
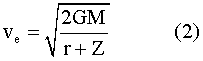
|
Height Z (km) |
Escape Speed (km/sec) |
|---|---|
|
0 100 200 300 400 500 |
11.18 11.09 11.01 10.93 10.84 10.75 |
| Table 1. Escape speed is dependent on altitude | |
Deciding on the height of the exobase is rather difficult because there is actually a transition region. But
“Let us take a value for the exospheric temperature T=1500 K, which is higher than average, and let us place the exobase at a height of 500km.”7
So particles need to be moving at 10.75 kilometers per second to escape from the earth’s gravitational influence. And this is independent of the mass of the particles.
Maxwell Distribution
As a next step we need to find the distribution of molecular velocities, so that we can find how many molecules can be expected to be traveling faster than the escape velocity. This is given by the Maxwell distribution8, the equation for which is:-
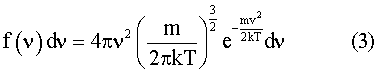
Results are shown for this function in figure 2. We have shown distribution curves for atomic hydrogen, atomic oxygen, and helium at 1500 K.

The most probable speed9 is given by the equation:
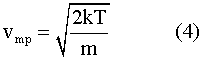
Although the formula for the Maxwell distribution looks complicated, it will be seen that the only variable in it is the square of the most probable speed. In other words, given a most probable speed, the probability curve is completely defined. And the area under the curve is unity. This means that if two distributions are displayed, and the most probable speed for B is twice that for A, then B will have exactly twice the spread of A, and half the height.
Now the plot shown in the skeptics’ article, which is shown as figure 3, is misleading in several ways. Most importantly, no units are shown on the x axis. (It is reasonable for there to be no y axis units). Clearly units should be shown for the plot to have any meaning, and so that we can compare against the known escape velocity. A curve is shown dashed, which purports to be at a somewhat higher temperature, but there is no indication of how much higher. If the most probable speed is doubled for the higher temperature, as seems to be the case, then it must be at four times the absolute temperature, i.e. If the solid curve represents 1500 K, then the dashed curve is for 6000 K.
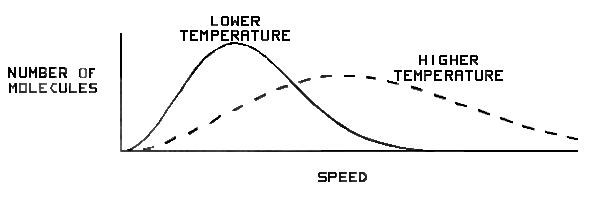
It is also misleading to group hydrogen and helium as being similar, and in a contrasting class to oxygen and nitrogen. In fact, helium is placed as a geometric mean in between hydrogen and oxygen, in the sense that the most probable speed for helium is twice that for oxygen, and half that for hydrogen, as shown in table 2. (This is because the square roots of their molecular weights are in the ratio of 1:2:4).
Table 2 also shows the molecular density of the most common gases at the exobase.10
Some Qualifications
| Molecule | Density (m–3) |
Molecular Weight (m) |
vmp at 1500 K |
|---|---|---|---|
| Atomic Hydrogen (H) | 8 x 1010 | 1 | 5 km/sec |
| Helium (He) | 2.5 x 1012 | 4 | 2.5 km/sec |
| Atomic Oxygen (O) | 2.7 x 1013 | 16 | 1.25 km/sec |
| Atomic Nitrogen (N) | 8 x 1011 | ||
| Nitrogen (N2) | 4.4 x 1011 | ||
| Oxygen (O2) | 8 x 109 | ||
| Argon (Ar) | 1 x 107 | ||
| Table 2. Molecular densities and most probable speeds at the exobase. | |||
It will probably be clear at this point that a number of assumptions have been made. This includes the unrealistic assumption that there is a sharp change at the exobase. Walker evaluates this and other approximations: To Walker —
But Fahr and Shizgal caution that“The arbitrary nature of the definition of the exobase is not a matter of concern (Jeans, 1925; Chamberlain 1963).”11
“The rigorous kinetic theory treatment of the transition region from collision-dominated to collisionless flow remains an outstanding objective.”12
“Chamberlain (1963) has shown that the neglect of collisions occurring above the exobase does not lead to an overestimate of the escape flux.”13
There is also apparently no problem in considering each type of gas molecule independently. That is, as if it was present alone.14
“A slight overestimate does result from the assumption that the Maxwellian distribution is fully populated in the region from which escape occurs. … The effect has been extensively studied (Hays and Liu, 1965; Chamberlain and Campbell, 1967; Chamberlain, 1969; Brinkmann, 1970, 1971; Chamberlain and Smith, 1971), and it appears that corrections to the expression for the escape flux derived above are generally smaller than 30%.”15
Vardiman doesn’t quite agree:
“Fahr and Shizgal imply that the rate of actual thermal escape is probably 70-80% of Jeans escape, although some calculations have been made that indicate the actual flux to be as little as 10–20% of the rate of Jeans escape. … In any case, Jeans escape is likely to be an upper limit to the thermal flux.”16
It should also be noted that the Maxwell speed distribution function alone, does not give the full story, as is implied by Ken Smith’s article. For some gases, diffusion is the limiting factor, rather than Jeans escape:
“Hydrogen, in fact, escapes into space almost as soon as it reaches the level from which escape is possible. The rate of loss of hydrogen is therefore limited to the rate at which hydrogen and its compounds are transported upwards from lower levels.”17
Estimated Helium Loss
To obtain the actual rate of loss of helium, we need to integrate the probability function for all molecules traveling upwards at a speed greater than the escape velocity. This has been done correctly by Walker, and is confirmed by Vardiman.18 The result is clear:
The characteristic time for helium escape at an average exospheric temperature of 1500 K is 60 million years19 or 70 million years20. But the magnitude of the source from the decay of radioactive elements has been estimated by a number of researchers 21,22,23,24,25. By dividing this flux into the column density of helium in the atmosphere (1.1 x 1020 cm-2)we obtain a residence time for helium of 2 million years, much less than the characteristic escape time.
“This result implies that the rate of Jeans escape at 1500 K is much smaller than the crustal source of helium. Since 1500 K is well above the average temperature of the exosphere, there appears to be a problem with the helium budget of the atmosphere.”26
Walker realizes that the influx of helium into the atmosphere vastly outweighs the loss to space by means of Jeans escape. But he is not happy with this result and immediately sets out to suggest various mechanisms that could perhaps account for this obvious problem with orthodox evolutionary science.
Other Loss Mechanisms
“MacDonald (1963, 1964) has evaluated the escape flux averaged over an entire 11-year cycle of solar activity, using satellite data on exospheric temperature. He finds an average escape flux of 6 x 104 cm-2sec–1, a factor of 30 less than the source. It is still possible, nevertheless, that the bulk of escape occurs during infrequent periods of unusually high temperature (Spitzer, 1949; Hunten 1973). Hunten has pointed out that if the temperature were to exceed 2000 K, diffusion would become the limiting process and the escape flux would be equal to the limiting flux, about 108 cm-2sec–1. To provide an average loss rate of 2 x 106 cm–2sec–1, these hot episodes would therefore have to occupy about 2% of the time.”27
Such hot episodes would dispose of the helium, but note that they have not been observed.
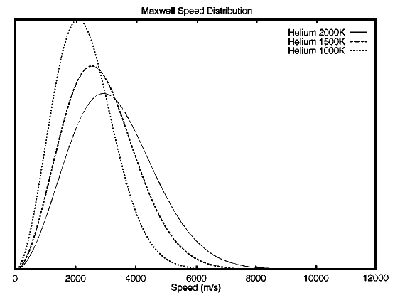
In figure 4 we show how the speed distribution for helium varies with temperature (1000–2000 K). Although there doesn’t appear to be a significant increase in the area under the tail of the curve above 10.75 km/s at 2000 K, it is apparently enough to make a difference. However—
“The average global exospheric temperature is 1037 K for average solar flux and magnetically quiet conditions.”28
There is the process of photochemical escape, which seems to be significant on Mars but not on earth.
“An alternative possibility is that there is a loss process for helium in addition to Jeans escape. Mechanisms other than Jeans escape have been proposed for the escape of gases from planetary atmospheres (Cole, 1966; Axford, 1968; Michel, 1971; Sheldon and Kern, 1972; Torr et al., 1974; Liu and Donahue, 1974a,b). Most of these are speculative and of undetermined evolutionary significance.”29
In this section we have referenced 11 papers in technical publications involving 13 different authors, who are trying to explain the “discrepancy” in the “helium budget.” Perhaps, they haven’t even considered the possibility that there is no problem with the helium figures because the earth is just not 4.5 billion years old.
Conclusion
It certainly seems that the creationist position is correct, on the basis of the latest observational evidence. As Chamberlain and Hunten admitted30 as recently as 1987, the helium escape problem “will not go away, and it is unsolved.”
This is a subject area which creationists will need to monitor closely. Quite complex calculations are involved, and data is needed from several disciplines, so there exists the possibility that authors may try to force results to fit their preconceived ideas. Therefore, if you are interested in this subject, it would be worthwhile obtaining the book by Larry Vardiman, which looks at this subject a lot more thoroughly than we have done here.
Acknowledgments
The Maxwell distribution curves were produced using the gnuplot software.
The book by Larry Vardiman was very helpful to me, particularly with his Bibliography of scientists who admit there is a problem.
David Malcolm has a Masters Degree in Engineering and works as a Computer Systems Officer for the Faculty of Engineering at the University of Newcastle, Australia. (in 1994).
Appendix: Symbols and Constants
| Meaning | Symbol | Value |
|---|---|---|
| Avogadro’s number | NA |
6.022 x 1023 mol-1
|
| Boltzman’s constant | k | 1.381 x 10-23 JK-1 |
| Earth radius | r | 6370 km |
| Earth mass | M | 5.9742 x 1024 kg |
| Gravitational constant | G | 6.672 x 10-11 m3kg-1s-2 |
| Molecular weight | m | |
| Temperature | T | K |
| Escape velocity | ve | |
| Most probable speed | vmp |
Sample
So that readers can check on the mathematics, we give here a sample
calculation. Evaluating the most probable speed for helium at 1500 K: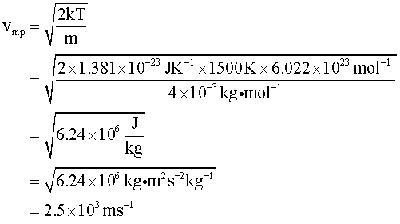
Bibliography
- AXFORD, W. I. (1968): The polar wind and the terrestrial helium budget. Journal of Geophysical Research 73:6855–6859.
- BRINKMANN, R. T. (1970): Departures from Jeans escape rate for H and He in the Earth’s atmosphere. Planetary and Space Science 18:449–478.
- BRINKMANN, R. T. (1971): More comments on the validity of Jeans escape rate. Planetary and Space Science 19:791–794.
- CHAMBERLAIN, J. W. (1963): Planetary coronae and atmospheric evaporation. Planetary and Space Science 11:901–960.
- CHAMBERLAIN, J. W. (1969): Escape rate of hydrogen from a carbon dioxide atmosphere. Astrophysical Journal 155:711–714.
- CHAMBERLAIN, J. W. and F. J. CAMPBELL (1967): Rate of evaporation of a non-Maxwellian atmosphere. Astrophysical Journal 49:687–705.
- CHAMBERLAIN, J. W. and G. R. SMITH (1971): Comments on the rate of evaporation of a non-Maxwellian atmosphere. Planetary and Space Science 19:675–684.
- COLE, K. D. (1966): Theory of some quiet magnetospheric phenomena related to the geomagnetic tail. Nature, 211, 1385–1387.
- HAYS, P. B. and V. C. LIU (1965): On the loss of gases from a planetary atmosphere. Planetary and Space Science 13:1185–1212.
- HUNTEN, D. M. (1973): The escape of light gases from planetary atmospheres. Journal of the Atmospheric Sciences 30:1481–1494.
- JEANS, J. H. (1925): The Dynamical Theory of Gases (Cambridge University Press, London).
- LIU, S. C. and T. M. DONAHUE (1974a): Mesospheric hydrogen related to exospheric escape mechanisms. Journal of the Atmospheric Sciences 31:1466–1470.
- LIU, S. C. and T. M. DONAHUE (1974b): Realistic model of hydrogen constituents in the lower atmosphere and escape flux from the upper atmosphere. Journal of the Atmospheric Sciences, 2238–2242.
- MacDONALD, G. J. F. (1963): The escape of helium from the earth’s atmosphere. Reviews of Geophysics and Space Physics 1:305–349.
- MacDONALD, G. J. F. (1964): The escape of helium from the earth’s atmosphere. In P. J. Brancazio and A. G. W. Cameron, eds., The Origins and Evolution of Atmospheres and Oceans, (John Wiley and Sons, New York), pp. 127–182.
- MICHEL, F. C. (1971): Solar wind induced mass loss from magnetic field-free planets. Planetary and Space Science 19:1580–1583.
- SHELDON, W. R. and J. W. KERN (1972): Atmospheric helium and geomagnetic field reversals. Journal of Geophysical Research 77:6194–6201.
- SPITZER, L. (1949): The terrestrial atmosphere above 300km. In G. P. Kuiper, ed., The Atmospheres of the Earth and Planets (Univ. of Chicago Press, Chicago), pp. 211–247.
- TORR, M. R., J. C. G. WALKER, and D. G. TORR (1974): Escape of fast oxygen from the atmosphere during geomagnetic storms. Journal of Geophysical Research 79:5267–5271.
Footnotes
- Cook, M. A. 1957. Where is the Earth’s radiogenic helium? Nature 179:213.
- Smith, K., 1986. Where is the Earth’s radiogenic helium. In: Creationism: An Australian Perspecive, M. Bridgstock and K. Smith (eds), The Australian Skeptics, Melbourne, pp. 20-21.
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York).
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), p. 151
- Szebehely, V. G. 1989. Adventures in Celestial Mechanics (University of Texas Press), pp. 59,65
- Vardiman, L. 1990. The Age of the Earth’s Atmosphere (Institute for Creation Research, San Diego). p. 13
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), p. 155
- Riedi, P. C. 1988. Thermal Physics (Oxford Uni. Press). p. 177
- Riedi, P. C. 1988. Thermal Physics (Oxford Uni. Press). p. 177
- COSPAR, 1988. COSPAR International Reference Atmosphere: 1986, Part I: Thermosphere Models (Pergamon Press, Great Britain), p. 153
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), p. 153
- Fahr, H.J. and B. Shizgal 1983. Modern exospheric theories and their observational relevance. Reviews of Geophysics and Space Physics, 21, 75–124. p. 118
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), p. 153
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), pp. 153–154
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), p. 153
- Vardiman, L. 1990. The Age of the Earth’s Atmosphere (Institute for Creation Research, San Diego), p. 23
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), p. 145
- Vardiman, L. 1990. The Age of the Earth’s Atmosphere (Institute for Creation Research, San Diego), pp. 19–24
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), p. 171
- Vardiman, L. 1990. The Age of the Earth’s Atmosphere (Institute for Creation Research, San Diego), p. 23
- MacDonald, G. J. F. 1963. The escape of helium from the earth’s atmosphere. Reviews of Geophysics and Space Physics 1:305–349.
- MacDonald, G. J. F. 1964. The escape of helium from the earth’s atmosphere. In P. J. Brancazio and A. G. W. Cameron, eds., The Origins and Evolution of Atmospheres and Oceans, (John Wiley and Sons, New York), pp. 127–182.
- Turekian, K. K. 1964. Degasssing of argon and helium from the earth. In P. J. Brancazio and A. G. W. Cameron, eds., The Origin and Evolution of Atmospheres and Oceans (John Wiley and Sons, New York), pp. 74–85.
- Axford, W. I. 1968. The polar wind and the terrestrial helium budget. Journal of Geophysical Research 73:6855–6859.
- Craig, H. and W. B. Clarke 1970. Oceanic 3He: Contribution from cosmogenic tritium. Earth and Planetary Science Letters 10:289–296.
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), p. 171
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), p. 172
- COSPAR, 1988. COSPAR International Reference Atmosphere: 1986, Part I: Thermosphere Models (Pergamon Press, Great Britain), p11
- Walker, J. C. G. 1977. Evolution of the Atmosphere (Macmillan Publishing Co., Inc., New York), p. 172
- Chamberlain, J. W. and D. M. Hunten 1987. Theory of Planetary Atmospheres, 2nd Ed. (Academic Press), p. 372
Recommended Resources

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- © 2024 Answers in Genesis