Unity

The Westmont College Horizon reported in 1976 that the faculty had defeated a proposal to return to an “inter-disciplinary, integrative (i.e. faith/practice)” program. According to the Horizon, . . .

. . . science is what you more or less know and philosophy is what you do not know. —Bertrand Russell1

The Westmont College Horizon reported in 1976 that the faculty had defeated a proposal to return to an “inter-disciplinary, integrative (i.e. faith/practice)” program. According to the Horizon, “some faculty members felt they were being pressured into doing something that was not possible in their particular field.” “Integration is not possible in mathematics,” said Dr. David Neu, Associate Professor of Mathematics. “In mathematics God’s revelation is silent. There is nothing to integrate . . . the mathematician is not seeking for truth . . . as far as mathematics goes there ain’t nuthin’ there.”2

It is not surprising that Dr. Neu might be led to assume that nothing is there in mathematics. Since 1850, this has been the majority position of the top professionals in his field, who turn some strange-sounding phrases when describing their discipline. For example, Bertrand Russell referred to mathematics as “the subject in which we never know what we are talking about, nor whether what we are saying is true.”3 Morris Kline called it “a body of knowledge” containing “no truths.”4 Henri Poincare’ defined it as “. . . the art of giving the same name to different things.”5 Alfred North Whitehead thought mathematics “to be the most original creation of the human spirit,”6 and to David Hilbert it became a meaningless, formal game.7

It is a mistake, however, to allow the power of these names in mathematics to give authority to conclusions in philosophy, and the foregoing statements are philosophical. Some people, Christians for example, tend to think that when a scientist wanders into philosophy, his conclusions warrant scrutiny. For the Christian, scientists are suspect in philosophy because, dealing so intimately with the creation, they fall into the Romans 1 category of those who knew God from His revelation in the creation, but did not honor Him as God. Kline complains “the true mathematical God refuses to reveal himself, and now mathematicians must question whether God exists.”8 They become futile in their speculations and are given over to outlaw minds. “There is a reason to question reason,” Kline warns.9 (Of course, we would then have to question the reasonableness of the statement: “There is a reason to question reason,” and so on; Kline’s proposition is inherently contradictory, but it’s catchy.) The philosophical base proposed by Russell was a “firm foundation of unyielding despair.”10

Why are there so many unifying elements such as sets, functions, and vectors, interlacing what initially appeared to be diverse ideas invented independently by different people at different times in different parts of the world?

In spite of their assumptions about the nature of mathematics, Russell and his compatriots, as I will show, talk mathematics and do mathematics as if this nothing was somehow something, at the least an art form which the mathematician creates as he pleases. There were two questions that mathematicians historically found difficult to answer from the perspective of mathematics-as-art, and with which their contemporary colleagues are still struggling.

First, why are there so many unifying elements such as sets, functions, and vectors, interlacing what initially appeared to be diverse ideas invented independently by different people at different times in different parts of the world? That there is such unity is well established. James J. Sylvester said,

Time was when all the parts of the subject were dissevered, when algebra, geometry, and arithmetic either lived apart or kept up cold relations of acquaintance confined to occasional calls upon one another; but that . . . is now happily at an end; they are constantly becoming more and more intimately related and connected by a thousand fresh ties, and we may confidently look forward to a time when they shall form but one body with one soul.11

Raymond L. Wilder talked about “the great generality . . . inherent in formal mathematical systems.” He went on to say that the evolution of mathematics “was to compel the development of a method which could encompass in a single framework of undefined terms and basic statements concepts like group and abstract space that were appearing in seemingly unrelated branches of mathematics.”12 (italics his)

Showing that unity eventually reigns even when chaos is expected, such as after daring mathematical innovation, Herbert Westren Turnbull says, “It is remarkable that, with these trends toward generalization in each of the four great branches of pure mathematics, the branches lose something of their distinctive qualities and grow more alike.”13

Further evidence of internal coherence in mathematics is given by Kline, who states, “The fact that a theorem developed to answer a question in one field so often turns out to be vital in a completely different one fills the history of mathematics with surprises.”14 Eric Temple Bell tells of

the intimate way Leopold Kronecker wove together three strands of his greatest interests—the theory of numbers, the theory of equations, and elliptic functions—into one beautiful pattern in which unforeseen symmetries were revealed as the design developed and many details were unexpectedly imaged in others far away. Each of the tools with which he worked seemed to have been designed by fate for the more efficient functioning of the others. Not content to accept this mysterious unity as a mere mystery, Kronecker sought and found its underlying structure in Karl Friedrich Gauss’ theory of binary quadratic forms.15

Yet Kronecker, who probably was a Christian, would admit only that, “The dear God has made the whole numbers, all the rest is man’s work.”16 Kronecker is not the only mathematician whose forays into philosophy could be typified by Winston Churchill’s description of political rival Stanley Baldwin: “Occasionally he stumbled over the truth, but hastily picked himself up as if nothing happened.”17

Employing words like “remarkable,” “surprise,” “unforeseen,” “unexpected,” and “mysterious,” Kline and Bell are tacitly admitting that the unity of mathematics shears the pins from their assumption that mathematicians invent mathematics. Even attempts by mathematicians to “force” disunity are rejected by the monolithic character of mathematics. For example, there is the “ . . . curious paradox [that] the closer we get to an absolutely patternless series, the closer we get to a type of pattern so rare that if we came on such a series we would suspect it had been carefully constructed by a mathematician and not by a random process.”18 It certainly appears that mathematics is an entity which someone designed, parts of which mathematicians discover. Often, they then become the poorest judges of the significance of their discoveries.

The theory of algebraic invariants, developed by Arthur Cayley and James J. Sylvester, is a case in point.

. . . the earliest instance of the idea appears in [Joseph-Louis] Lagrange, from whom it passed into the arithmetical works of Gauss. But neither of these men noticed that the simple but remarkable algebraic phenomenon before them was the germ of a vast theory. Nor does George Boole seem to have fully realized what he had found when he carried on and greatly extended the work of Lagrange.19

If there is any topic one would expect to have been finally purged of surprises, it is the elementary geometry of the triangle and circle which, even in the 19th century, had been extant for hundreds of years. That century, however, “witnessed an astonishing reopening of this study. It seems that this field of investigation must be unlimited.”20

Philip E.B. Jourdain’s assessment of the situation has been labeled “old-fashioned” and “quaint.” It is also supported, rather than devastated, by the unity found in mathematics, as anyone will see who is able to set aside what C.S. Lewis called “chronological snobbery.” Jourdain said,

. . . the nature of Mathematics is independent of us personally and of the world outside, and we can feel that our own discoveries and views do not affect the Truth itself, but only the extent which we or others see it. Some of us discover things in science, but we do not really create anything in science any more than Columbus created America. . . . Some philosophers have reached the startling conclusion that Truth is made by men, and that Columbus created America; but common sense . . . is . . . above being flattered by philosophical persuasion that it really occupies a place sometimes reserved for an even more sacred being.”21

Charles Hermite, sounding like a Jourdainian echo, said,

I believe that the numbers and functions of analysis are not the arbitrary product of our spirits; I believe that they exist outside of us with the same character of necessity as the objects of objective reality, and we find or discover them and study them as do the physicists, chemists, and zoologists.22

Jacques Hadamard, whom Kline calls “the leading French mathematician of this century,” said, “Although the truth is not yet known to us, it preexists and inescapably imposes on us the path we must follow under penalty of going astray.”23 Even Bertrand Russell, referring to “our certainty that the facts must always conform to logic and arithmetic,” claimed that “to say that logic and arithmetic are contributed by us does not account for this.”24

Non-Euclidean Geometry

Before 1850, God was often credited with being the inventor of mathematics. Then the development of the non-Euclidean geometries reached adolescence and caused mathematicians, as Morris Kline says, “to see that they must stand on their own feet. They were not recording nature; they were interpreting.”25

It is true that if any portion of mathematics could be classified as human invention, it is non-Euclidean geometry. But it is obviously not true that the “inventors” were “interpreting” nature, since these geometries were unveiled during purely intellectual exercises in abstraction, beginning with, “What if . . . ?” They were by-products of unsuccessful attempts to prove that Euclid’s fifth postulate was dependent on his others. One technique was to negate the postulate and examine the resulting implications for a contradiction.

Before 1850, God was often credited with being the inventor of mathematics.

Euclid’s postulate is equivalent to the assumption that in a plane, through a given point not on a given line, there is only one parallel to the line. This, in turn, is equivalent to assuming that the sum of the measures of the three interior angles of a triangle is equal to the measures of two right angles. The resulting geometry is sometimes labeled “parabolic.”

John Bolyai and Nikolai I. Lobachevsky independently developed a list of non-contradictory statements—a new geometry—by postulating at least two parallels to the line or, correspondingly, that the sum of the angles of a triangle is less than two right angles. This geometry is called “hyperbolic.” Later Georg F.B. Riemann discovered another geometry (elliptic) by assuming that there are no parallels, or that the sum of the angles in a triangle is more than two right angles. This is the geometry on a sphere. (Riemann actually changed not only Euclid’s fifth postulate but also at least one other of Euclid’s implicit assumptions.)

These geometries, with their contradictory hypotheses but internally consistent structures, seemed a flaw in the unity of mathematics. They appeared to support the notion that a

mathematician is entirely free, within the limits of his own imagination, to construct what worlds he pleases. What he is to imagine is a matter of his own caprice; he is not discovering the fundamental principles of the universe nor becoming acquainted with the ideas of God.26

Denizens of the mid-nineteenth century world of mathematics perhaps could be excused their lack of vision in their eagerness to parlay the unique new geometries into a claim of ownership on all mathematics. After all, if the unity of mathematics was a fiction, then maybe men really did think it up on their own. Under this assumption, it should reflect freedom and fragmentation, of which new geometry was “Exhibit A.”

Peering over the edges of history, Kline should know better, and as it turns out, he does. In his book, Mathematics in Western Culture, a few pages on from his previous statement, he admits

. . . it is possible to erect projective geometry on an axiomatic basis in such a way that the theorems of the other three geometries result in specialized theorems of projective geometry. In other words, the contents of all four geometries are now incorporated in one harmonious whole.27

He is alluding to the work of Felix Klein who, building on foundations laid by Cayley and Karl G.C. Von Staudt, proved there are no contradictions among the “other three geometries” if the mathematical contexts are kept in mind. To use “parallel” in different frames of reference without identifying them (as some mathematicians have done) is tantamount to using a word like “drive” without giving the background—golf? roadway? car? basketball? cattle? The difficulty vanishes when the contextual framework is recognized. As “Cayley exclaimed, ‘Projective geometry is all geometry.’”28

Further evidence both for the unity of mathematics and for the view that mathematicians really are following the vapor trails left by the course of someone’s powerful thought, without actually knowing where the trails are leading, comes from H.W. Turnbull. After mentioning that Von Staudt “has revealed the solid foundations common to all types of geometry,” Turnbull says,

The really remarkable thing about it all is that Pappus and Desargues had actually hit upon the fundamental theorems of geometry in spite of using proofs involving unnecessary assumptions. [They] had given wrong reasons for the right results, and the same thing frequently happened in calculus.29

Quaternions

In Mathematics: The Loss of Certainty, Kline claims that Hamilton’s “invention” of quaternions was another event which drained truth from mathematics, since it introduced non-commutability to algebra. But quaternions simply opened the door to the more general vector algebra and, Kline admits, “did not challenge the correctness of the real number system.”30

Freedom

More than any other person, possibly excepting the synthetical Nicholas Bourbaki, Eugene Wigner writes honestly of the conflict posed by the unity of mathematics in the face of humanistic assumptions about its origin. According to Nobel Prize winner Wigner, “The great mathematician fully, almost ruthlessly, exploits the domain of permissible reasoning and skirts the impermissible. That his recklessness does not lead him into a morass of contradictions is a miracle in itself.” Wigner then adds the cryptic observation, “It is hard to believe that our reasoning power was brought, by Darwin’s process of natural selection, to the perfection it seems to possess.”31

If mathematics is already thought out and constructed by someone, it is logical that there would be no contradictions

Many mathematicians, like Wigner, believe mathematics is a unified entity “out there”—they are Platonists. However, they do not feel impelled, as the Christian does, to account for the origin of this entity, and are content to label it a miracle. The Christian position is rational here. If mathematics is already thought out and constructed by someone, it is logical that there would be no contradictions; the constraints imposed on the structure by the original thinker preserve its unity and integrity, and nudge the mathematician clear of the “morass of contradictions.”

Physical chemist Gilbert N. Lewis, while not giving any credit to God, nevertheless admitted,

We cannot avoid the thought that having embarked upon a certain line of mathematical inquiry, while we appear to have preserved the utmost of personal freedom, we seem bound to follow certain paths and make and remake certain discoveries . . .32

G.H. Hardy, even though he regarded God as his personal enemy, had to agree. He stated, “I believe that mathematical reality lies outside us, that our function is to discover or observe it, and that the theorems which we prove, and which we describe grandiloquently as our ‘creations’ are simply notes of our observations.”33

In spite of viewpoints like Hardy’s, most mathematicians, contemplating the non-Euclidean geometries with their seemingly contradictory hypotheses, are led to assume that any statement may be hypothesized. John W.N. Sullivan speaks for a host of mathematicians when he says,

The further development of non-Euclidean geometry and its application to physical phenomena by Einstein have shown that Euclid’s geometry is not only not a necessity of thought but it is not even the most convenient geometry to apply to existing space. And with this there has come, of course, a profound change in the status we ascribe to mathematical entities, and a different estimate of the mathematician’s activities. We can start from any set of axioms we please, provided they are consistent with themselves and one another, and work out a branch of mathematics. The primary definitions and postulates are not given by experience, nor are they necessities of thought.34

So Russell was not trying to be funny— wry perhaps—when he said mathematicians don’t know what they are talking about nor whether it’s true. Kline meant what he said about mathematics being a “body of knowledge” containing “no truths.”35 Richard Dedekind was serious when he claimed that “numbers are free creations of the human mind,”36 and so was Georg Cantor, who stated, “The essence of mathematics lies in its freedom.”37 C.J. Keyser, to the question, “Is it true?” answered, “The mathematician as a man does not know although he cares. Man as mathematician neither knows nor cares.”38

The weakness here is that while proclaiming their freedom to hypothesize whatever tickles their fancy, most mathematicians admit that not every statement should be postulated. As Douglas Gasking claimed, “Mathematics does depend on and reflect the nature of the world at least to this extent, that we would find certain systems enormously inconvenient and difficult to use, and others relatively simple and handy.” Even though he believes this convenience “depends on our psychological make-up” rather than the “external world,” Gasking admits,

Using one sort of arithmetic or geometry, for example, we might find that our physics could be reduced to a logically neat and simple system, which is intellectually satisfying whereas using different arithmetics and geometries, we should find our physics full of very complicated ad hoc hypotheses.39

Concurring, Einstein said,

A man engaged in solving a well designed word-puzzle may, it’s true, propose any word as the solution; but there is only one word which really solves the puzzle in all its forms. It is an outcome of faith that nature . . . takes the character of such a well formulated puzzle. The successes reaped by science do, it is true, give a certain encouragement for this faith.40

Mathematics or Merely Mathematical?

Einstein and Gasking are tacitly admitting that not everything mathematical (logically valid) is truly mathematics. The existence of valid systems having false conclusions does not imply, as Russell, et al., would have it, that there exist no valid systems with true conclusions.

A statement by Klein is apropos. He said,

You can hear often from non-mathematicians, especially from philosophers, that mathematics consists exclusively in drawing conclusions from clearly stated premises; and that, in this process, it makes no difference what these premises signify, whether they are true or false, provided only that they do not contradict one another. But a person who has done productive mathematical work will talk quite differently.41

Klein’s view is supported by Richard Courant and Herbert Robbins in their book, What is Mathematics? They warn that

a serious threat to the very life of science is implied in the assertion that mathematics is nothing but a system of conclusions drawn from definitions and postulates that must be consistent but otherwise may be created by the free will of the mathematician. If this description were accurate, mathematics could not attract any intelligent person. It would be a game with definitions, rules, and syllogisms, without motive or goal. The notion that the intellect can create meaningful postulational systems at its whim is a deceptive half-truth. Only under the discipline of responsibility to the organic whole, only guided by intrinsic necessity, can the free mind achieve results of scientific value.42

Unity Unexpected

One could believe the calculus was a work of art produced by the free will of man if one could believe the possibility of a symphony arising from the scores of a number of composers who supposed they were writing only tone poems for solos or chamber groups. This symphony comes together without changing even the key, though the artists wrote during hundreds of years in different corners of the globe without the knowledge of each others’ work.

To discover many of his theorems, Archimedes used what, in a letter to Eratosthenes, he called, “The Method.” He then proved these theorems by the technique of exhaustion. This “method,” which he kept secret because he was not able to make it rigorous, was essentially what we know as integration.43 As Felix Klein said, “One can give numerous examples of mathematicians who have discovered theorems of the greatest importance, which they were unable to prove.”44

Morris Kline points out that “during the centuries in which the major branches of mathematics were built up there was no logical development for most of it. Apparently the intuitions of great men are more powerful than their logic.”45 One example of “mathematical prescience” is Newton’s rule for the discovery of imaginary roots of equations, which was not proved until Sylvester did it in 1865. Along this line, Philip Jourdain said, “Mathematicians thought . . . that imaginaries, though apparently uninterpretable and even self-contradictory, must have a logic. So they were used with a faith . . . that . . . was only justified much later.”46

Jourdain had further cogent observations on this subject: “In mathematics it has . . . always happened that conceptions have been used long before they were formally introduced, and used long before this use could be logically justified or its nature clearly explained. The history of mathematics is the history of a faith whose justification has been long delayed, and perhaps is not accomplished even now.”47 Jourdain also claimed, “It is a curious fact that mathematicians have so often arrived at truth by a sort of instinct.”48 Earnest Nagel and James R. Newman agree, stating,

The use of rules and theorems is an all but unconscious process . . . like Moliere’s M. Jourdain, who spoke prose without knowing it, mathematicians have been reasoning without knowing their reasons. Modern students have had to show them the tools of their craft.49

Jourdain (no relation to Moliere’s) cites as an example the beautiful unity between geometry and algebra. Specifically, he points out that the curves the ancient Greek geometricians chose to study were sections of two equal cones with the same axis, whose only points of intersection were their vertices. As it turned out much later, these are the very curves (and the only ones) determined by algebraic equations of the second degree in two variables. Jourdain uses words like “mystery,” “lucky” and “chance” to describe this phenomenon.

Similarly, in calculus, the integral was discovered before the derivative, and they developed for some time along parallel paths. They seemed to be completely different ideas. The big surprise (to those who thought them separate works of art) came when it was observed that they were actually inverses of each other. Though appearing to bounce around in history at the whim of its “creators,” mathematics truly hangs together.

Simultaneous “Inventions”

Spotlighting this fact are the numerous simultaneously produced identical “inventions.” As Gilbert N. Lewis points out,

. . . the two geometries which were published independently and almost simultaneously, one by the Russian Lobachevski, and the other by the Hungarian Bolyai, were so nearly alike that they seem like different drafts of the same composition. Similarly, [William Rowan] Hamilton and [Hermann] Grassman wrote at the same time those papers which were to become the foundation of modern vector analysis.50

William Fielding Ogburn cites many other cases of simultaneous, independent discoveries, the probability that they are coincidental “inventions” being inversely proportional to the length of the list. Included are: Law of Inverse Squares by Newton and Halley, Logarithms by Burgi and Napier/Briggs, the Calculus by Newton and Leibniz, Principle of Least Squares by Gauss and Legendre—in fact, Gauss said, “It seems to be my fate to concur in nearly all my theoretical works with Legendre”51—Contraction Hypothesis by H.A. Lorentz and Fitzgerald, the double Theta functions by Gopel and Rosehain, the rectification of the semi-cubal parabola by Van Heauraet, Neil and Fermat, and the geometric law of duality by Oncelet and Gergone.52 It is as if a diverse group of artists, supposing they were independent and free, compared their works at a show to find they were identical, down to each brush stroke and nuance of color.

Is It Culture?

Some have attempted to explain away these annoying “coincidences” by claiming mathematics to be simply a product of culture. Our minds are like pipes, and the cultural “soup” flows through them. Since there are quite a few mathematicians, it is not surprising that two would turn the spigot at the same time. And since the “soup” is pretty much the same for everybody, it is not surprising that the same mathematics flows forth.

There is little agreement as to the meaning of “culture.” The simplest characterizations are “group,” “group mystique,” or “group dynamic.” Does mathematics flow out of scholastic, governmental, or ecclesiastic interaction, or it is independent of the machinations of any group? Davis and Hersh, in their book, The Mathematical Experience, take a middle-of-the-road position, claiming they “know in [their] bones that culture makes a difference.”53

One fact which militates against this approach is the discovery of “acultural” mathematics, that is, mathematics preceded by not the slightest cultural hint. This was true of the “invention” of logarithms, which

came upon the world as a bolt from the blue. No previous work had led up to it, nothing had foreshadowed it or heralded its arrival. It stands isolated, breaking in upon human thought abruptly without borrowing from the work of other intellects or following known lines of mathematical thought. It reminds me of those islands in the ocean which rise suddenly from great depths and which stand solitary with deep water close around all their shores.54

Even though the advent of the logarithm was startlingly abrupt, minimizing the possibility that it was an overflow of the culture, the unity of mathematics remained serene. While machines have made computation with logarithms obsolete, logarithmic functions and their inverses, the exponentials, are of critical value to modern mathematical science. This is true even though “one of the anomalies in the history of mathematics is the fact that logarithms were discovered before exponents were in use.”55

E.T. Bell provides another case in point: Charles Hermite’s solving of the general equation of the fifth degree by using elliptic functions. “It is almost impossible,” says Bell, “to convey to a non-mathematician the spectacular brilliance of such a feat. To give a very inadequate simile, Hermite found the famous lost ‘chord’ when no mortal had the slightest suspicion that such an elusive thing existed anywhere in time and space . . . totally unforeseen . . . ”56 Hermite, for one, did not give culture the credit for mathematical development. “There exists,” he asserted, “a world which is the collection of mathematical truths, to which we have access only through our intellects, just as there is the world of physical reality; the one and the other independent of us, both of divine creation . . . ”57 Dr. Bell reminds us also of the Hindu, Srinivasa Ramanujan, who

arrives unexpectedly out of nowhere, even expert analysts hail him as a gift from Heaven: his all but supernatural insight into apparently unrelated formulas reveals hidden trails leading from one territory to another, and the analysts have new tasks provided for them in clearing the trails.58

G.H. Hardy, who was Ramanujan’s mentor/student, said, “[Ramanujan] worked, for most of his life, in practically complete ignorance of modern European mathematics . . . ” “He had no real teaching at all; there was no one in India from whom he had anything to learn. He can have seen at the outside three or four books of good quality . . . ”59

To the Christian mind, it becomes increasingly apparent that Jourdain was right when he said, “ . . . but Mathematics is eternal and unchanging, and therefore had no history—it does not belong, even in part, to Euclid or Newton or anybody else, but is something which is discovered, in the course of time, by human minds.”60

Instinct & Inspiration

The facts support Newman and Nagel’s claim that mathematical truth is often arrived at by a sort of instinct. “As a young man, Gauss would be ‘seized’ by mathematics. Conversing with friends, he would suddenly go silent, overwhelmed by thoughts beyond his control, and stand staring rigidly oblivious to his surroundings.”61 And it “flashed upon” George Boole “as he was walking across the field, that besides the knowledge gained from direct observation, man derives knowledge from some source indefinable and invisible.”62

Since similar inspiration strikes great writers, artists, or composers, it is easy for a mathematician like Hardy to suppose himself included in their ranks. He claimed that

A mathematician, like a painter or poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with ideas . . . A mathematician . . . has no material to work with but ideas, and so his patterns are likely to last longer . . . The mathematician’s patterns, like the painter’s or poet’s, must be beautiful; the ideas, like the colors or the words, must fit together in a harmonious way. Beauty is the first test . . .63

Problem: in art “the colors or words must fit together in a harmonious way” only on each canvas, or in each book or score. Most artists would disagree that even “internal” harmony is the hallmark of an artistic work, preferring to use words like “integrity” or “communication.” The ideas of the mathematician, on the other hand, not only must fit together in his or her individual effort but also must mesh precisely with every other mathematician’s work, past, present, and future. The monolithic quality of mathematics simply necessitates interpreting mathematical truth as discovery rather than invention or art.

Even Kline, for whom mathematics contains no truth, talks as if it were some thing to be discovered. For example, to describe “the choice of a set of axioms,” he uses the analogy of “the purchase of a piece of mining land. The riches,” he says, “are all there.”64

Natural & Simple

One so often reads of mathematicians sifting a morass of ideas until at last coming upon the “natural” or “right” one.

Hamilton, one of the great mathematical geniuses of the 19th century, records with Irish exuberance how he struggled for 15 years to invent a consistent algebra to do what was required until a happy inspiration gave him the clue that a x b is not equal to b x a in the algebra he was seeking.65 (italics mine)

Gauss, “after many false starts which led to intolerable complexity” in higher number congruences and corresponding laws of reciprocity, “discovered the ‘natural’ [Gauss’ word] way to the heart of his problem.”66

Both Kronecker and Karl W. Weierstrass, working in algebra and analysis respectively, never stopped until they were sure they had found the best, or natural, way of development.67 Hardy notwithstanding, I believe that “beauty” is not a test at all, but simply the result when true mathematics is discovered. “The useful combinations,” observed Poincare, “are precisely the most beautiful . . . ”68

As J.A. Dieudonne said, referring to the work of N. Bourbaki (Bourbaki is really “them,” a group of French mathematicians, mainly Parisians, whose only rule is that a member must be under 50 years of age),

Bourbaki sets off . . . from a basic belief, an unprovable meta-physical belief we willingly admit. It is that mathematics is fundamentally simple and that for each mathematical question there is, among all possible ways of dealing with it, a best way, an optimal method.69

Dieudonne later made the remarkable statement that while each mathematician feels “he is working with something real . . . this sensation is probably an illusion.” Dieudonne admits, however, that this “illusion” of reality “is very convenient.”70

His thinking parallels Albert Einstein’s, who said,

To him who is a discoverer in this field (theoretical physics) the products of his imagination appear so necessary and natural that he regards them, and would like to have them regarded by others not as creations of thought but as given realities.71

Einstein also claimed,

The historical development has shown that among the imaginable theoretical constructions there is invariably one that proves to be unquestionably superior to all others. Nobody who really goes into the matter will deny that the world of perceptions determines the theoretical system in a virtually unambiguous manner.72

Herman Weyl agrees, stating,

An outstanding example is Euclidean geometry, which was proved by geodetic and astronomical precision measurements to be much more exactly valid than could have been conjectured on the basis of the experiences which led to its erection. But this is far from being the only example of such a confirmation of the principle of simplicity. There is an abundance of similar cases in physics.73

The following comparison of mathematics and art by H.W. Turnbull is about all that can be claimed rationally.

The greatest mathematics has the simplicity and inevitableness of supreme poetry and music, standing on the borderland of all that is wonderful in Science, and all that is beautiful in Art. Mathematics transfigures the fortuitous concourse of atoms into the tracery of the finger of God.74

It is questionable whether “supreme” art is either simple or inevitable, but Turnbull recognized that “the borderland” is as close as mathematics gets to art, and believed that only God is big enough to impose a unity on the mathematical thoughts with which mathematicians are “seized.”

What Is Meant by “Creation”?

The word “create,” for many mathematicians, really refers to processes of discrimination, selection, and arrangement, even style. To these areas, mathematicians do bring a creativity akin to the best in art. After calling mathematics a “creative endeavor,” Kline says, “In divining what can be proved, as well as in constructing methods of proof, mathematicians employ a high order of intuition and imagination.”75 Attributing this meaning to “creative” would not disturb most theists. Nor would Henri Poincare’s definition, from a speech to the Psychological Society in Paris: “A mathematical proof is not a mere juxtaposition of syllogisms: It is syllogisms arranged in a certain order, and the order is more important than the elements themselves.”76 (italics his)

Then Poincare (unintentionally?) exposes the difference between artistic and mathematical “creation.”

Mathematical creation however does not consist merely in making new combinations of things already known; anyone [artist] could do that, but the combinations thus made would be infinite in number and most of them entirely devoid of interest. To create consists precisely in avoiding useless combinations and in making those which constitute only a small minority. Invention is discernment, choice.77

It is interesting that, in his book, Science and Method, Poincare duplicates this portion of his lecture almost word-for-word, except that he replaces the word “invention” with the word “discovery.”78 And Morris Kline faces no argument from Christians when he equates “creating” or “inventing” mathematics with:

the patient, hard digging which must be performed, the careful sifting of the precious metal from the the base rock, the value and beauty of the treasure obtained, and the pleasure and exhilaration of accomplishment.79

The problem comes when misplaced pride of ownership in a piece of research blurs the distinction between the mathematics excavated and the tools used for its excavation, to borrow Philip Jourdain’s analogy.80 Expressing the situation accurately, G.K. Chesterton said, “The difference between the poet and the mathematician is that the poet only asks to get his head into the heavens. It is the logician [mathematician] who seeks to get the heavens into his head.”81 This is why there are many different poetic expressions of “the heavens,” but just one mathematics.

Unlikely Partners

The unity of mathematics is highlighted by equations which connect unlikely partners in surprising ways. The star of these equations is a statement known as Euler’s equation, which combines the real number constants e and π, the imaginary unit, √−1 (symbolized by “i”), with the additive and multiplicative identities to give e^iπ + 1 = 0. For years these numbers led their own lives and appeared unrelated to each other. After all, e and π are special irrationals (see Transcendentals, below), i isn’t even in the real number system, and 1 and 0 are “old hat” integers.

The star of these equations is a statement known as Euler’s equation.

e and 1 are also linked to the set of prime numbers by the Prime Number Theorem. It can be proved that the limit of the ratio (π(N)/N)/(1/log_eN) is 1 as N→∞, where π(N) is the number of primes between 1 and N.82 Constance Reid calls this “one of the most totally unexpected things in all mathematics!”83

Although the digits in their decimal expressions follow no pattern, the mavericks e and π can be laid out in beautiful integer mosaics such as “the striking, simple connection between π and the set of all odd numbers:

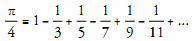.”84

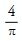, the reciprocal of .

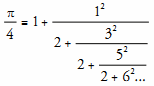Others are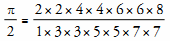

and 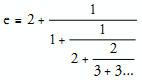.85

Euler86 also proved that .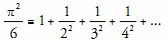

David Berlinski, in his book, The Advent of the Algorithm, says this series revealed “a glittering connection between geometry and arithmetic, the connection all the more glittering because all the more arbitrary. Why π? Why π²? Why 6? Why the ratio?

Why indeed.”87

He says that he does “not know the answers, not then, not now. All that the mathematician in me can see is the jewel.” The Christian knows that God is the only One with enough power to impose this “arbitrary” unity on mathematics, and delights to behold His glory radiating from this particular “jewel.”

What about the reciprocal of Berlinski’s gem? I wonder what his reaction was when he discovered that 6/π² is the probability that 2 positive integers, taken at random, are relatively prime.88

I can’t resist giving you one more quote from Berlinski which spotlights the “glittering” unity of the structure of mathematics. He calls the “fusion” between λ(lambda)-definable functions and recursive functions “utterly astonishing. No other word will do. . . . far and away separate stars . . . contrary to every expectation . . . are inextricably fused . . . and really revolving around a . . . common core.” [Berlinski, p. 179]

Transcendentals

e and π are the most famous members of a set of numbers called “transcendentals,” which cannot be roots of algebraic equations with rational coefficients. There are also transcendental functions, like sine, which cannot be expressed by a finite number of algebraic operations. Alluding (unintentionally, no doubt) to the motivation which produced the revealing label, “transcendental,” Bell says,

But it is probably a much more difficult problem to prove that a particular suspect, like e or π, is or is not transcendental, than it is to invent a whole infinite class of transcendentals: the inventive mathematician dictates—to a certain extent—the working conditions, while the suspected number is entire master of the situation, and it is the mathematician in this case, not the suspect, who takes orders he only dimly understands.89

Numbers such as e and π serve also as remarkable testimonials to the marriage of mathematics and nature. From the thin air of relativity and number theory to the most common measurement techniques, their influence is pervasive. Applications of the ubiquitous pair in statistics, probability, biology, sociology, and finance seem far removed from their everyday geometrical setting. It certainly appears that these numbers are unifying elements in an overall nature/mathematics scheme for which no human being is powerful enough to receive the credit.

Algebra, Geometry & Arithmetic

As anyone knows who has studied coordinate geometry, algebra and geometry are closely related; in fact, they are structurally identical, even though for many years they were thought to be completely independent of each other. Geometry is also unified with number theory in striking ways. For example, “the limiting value of two successive terms of Fibonacci numbers, as we go out indefinitely, is precisely the ratio of the side of the regular inscribed decagon to the radius of the circumscribing circle.”90

Analysis and Number Theory

William Dunham points out that even the techniques of the “continuous, ‘flowing’ phenomena of calculus/analysis,” which “require the rich continuum of the real number system,” can be applied to number theory, which “is as discrete as it gets. The integers are separated, isolated entities which require a very different set of tools.” Dunham calls this relationship “peculiar.” The Christian says, “I am not surprised.”91

Infinity

“Infinite” is a term used in every branch of mathematics, part of the “glue” welding the parts into coherent unity. Nothing in human experience gets one as close as does mathematics to the meaning of infinity. Even a child tastes its flavor when he realizes there is no “biggest” number, a fact the child himself can “prove” by adding 1 to any nominee for “biggest.” The “inventive” mathematician is beyond his depth when dealing with infinity; despite his best efforts it will not “behave,” and leads him to embarrassment and consternation. James Pierpont pointed out the two faces of the problem when he said,

As in the days of Newton and Leibnitz, so now the notion of infinity is our greatest friend; it is also the greatest enemy of our peace of mind. We may compare it to a great waterway bearing the traffic of the world, a waterway however which from time to time breaks its bounds and spreads devastation along its banks. Weierstrass taught us to believe that we had at last thoroughly tamed and domesticated this unruly element. Such however is not the case; it has broken loose again. Hilbert and Brouwer have set out to tame it once more. For how long? We wonder.92

As Nagel and Newman bring out in their essay on Kurt Goedel’s work,

In attempting to solve the problem of consistency one notices a recurrent source of difficulty. It is encountered whenever a non-finite model is invoked for purposes of interpretation . . . the model itself will have to mirror the infinity of elements postulated by the axioms. The truth (and so the consistency) of the set cannot therefore be established by inspection and enumeration.93

I think it is evident that man is dealing in mathematics with something bigger than his thinking. Their confusion evident, Nagel and Newman go on to say,

In certain areas of mathematical research, in which assumptions about infinite domains play central roles, radical contradictions (or “antinomies”) have turned up, despite the intuitive clarity of the notion involved in the assumptions, and despite the seemingly consistent character of the intellectual constructions performed . . . the apparent clarity of even such an elementary notion as that of class, does not guarantee the consistency of the system built on it . . . the intellectual construction . . . of non-finite models generally involves the use of possibly inconsistent sets of postulates . . . growing apprehension . . . that established mathematical systems were infected by contradictions, led to new attacks upon the problem.94

Kurt Goedel showed, however, that none of the “new attacks” did, or could ever, bridge the abyss from finite to infinite, that the consistency of any deductive system which encompasses all of arithmetic can never be proved. Even more astounding, he showed that no set of axioms would be sufficient to account for the mathematical truth in any one branch of mathematics. There are always theorems which do not follow from the axioms, but which can be shown to be true by informal reasoning. According to Kline, “while Brouwer made clear that what is intuitively certain falls short of what is proved in classical mathematics, Godel showed that what is intuitively certain extends beyond mathematical proof.”95

Perhaps mathematics really is God’s thought, as was the commonly accepted view before 1850. The paradoxes wrought by infinity in set theory then would be expected and, if not explained, would be incomprehensible in a way we could comprehend. To use C.S. Lewis’ phrase, “ . . . if there exists something beyond personality it ought to be incomprehensible in that sort of way.”96

I believe that the infinite-personal God of the Bible exists beyond human personality. I believe that, in the example previously mentioned involving the Fibonacci numbers and geometry, God may well be telling us:

I will give you some geometry (the side of the regular decagon and the radius of the circumcircle) which you can see, measure, and compute with, but just to remind you that mathematics is all one and Mine, I will also show you an infinite sequence of numbers you can not even write down, but which you can prove is exactly equal to the ratio of the side to the radius.

A similar example is given by the equation: .999 . . . = 1. Even if there were a trillion nines following the decimal point, the “equals” sign could not be used; the result depends on there being infinitely many nines. I believe the right side of the equation is “ours,” a gift from Him, one of the most important and useful of numbers. The left side is God’s alone, a number we can not write down, but which we can prove is exactly equal to 1.

Infinity is God’s unique prerogative, yet here it glimmers at the core of mathematics.

Infinity is God’s unique prerogative, yet here it glimmers at the core of mathematics. No wonder mathematicians feel compelled to make statements similar to R.L. Wilder’s: “. . . the research mathematician sometimes acquires a feeling that he is being led by the concepts instead of the other way around!”97

Summary

Forcing Berlinski to ask, “Why?”, the unity of mathematics is to Dunhuam “peculiar,” to Turnbull “remarkable,” to Kline “surprising,” to Bell “unexpected” and “mysterious,” to Wigner “a miracle,” to Howard Eves “astonishing,” and to Jourdain “an exceedingly lucky chance.” If the unified character of mathematics cannot be accounted for rationally from the perspective of mathematics-as-art or invention, those of this persuasion should ask themselves if their position is realistic.

Others, including some Christians, who recognize that mathematics is “out there” to be discovered, but who feel no compulsion to account for it, are obviously able to exist without a unified field of knowledge. The writing of many of them, however, reveals that theirs is a precarious environment, reminiscent of Matthew Arnold’s “darkling plain, swept with confused alarms of struggle and flight,” which I believe stems from ignoring the foundational questions of origin, nature, and purpose.