Chapter 4
The Nature of Mathematics
Truth & the Transcendent
If there is “something there” in mathematics, the Christian cannot escape the consequences of the universal quantifiers which saturate Colossians 1:15–20.
Just before the Nazis invaded France, many French people subscribed to a fund to plant rose bushes in front of the pill boxes on the Maginot Line to make life pleasanter for the troops stationed there; some people interpreted this to be a hope that if the Maginot Line were covered up with rose bushes, maybe the war would go away. —“The Sorrow and the Pity”1
True education is unveiling the all-glorious God of creation. . .in the creation. —Dr. Mark Fakkema2
If there is “something there” in mathematics, the Christian cannot escape the consequences of the universal quantifiers which saturate Colossians 1:15–20:
It was through Christ that everything was created in heaven and earth, the seen and the unseen . . . ; all things have been created through Him and for Him . . . through Him all things are held together . . . that He alone should stand first in everything . . . through Him He might reconcile to Himself all things.(italics mine)
1 Corinthians 8:6 directs attention to the
“one God who is the source of all things and
the goal of our living.
” And from Romans 1:20,
we learn that “since the creation of the
world His invisible attributes, His eternal
power and divine nature, have been clearly
seen, being understood through what has
been made . . .
”
Compromise is impossible.
In a class
at the University of Oregon, a mathematics
professor, half-serious, repeated “Kronecker’s
Cliche,” that though God made the integers,
all else was man’s doing. After class, he readily
admitted there was no way that Kronecker
could be correct. Because of the obvious
internal solidarity of mathematics, and its
“peculiar” relationship with nature, he agreed
that either none of mathematics originates
with God or it all does.
The patina of secularization with which mathematics has become encrusted must be polished away so that its true, God-reflecting nature shines through.
If mathematics is the basic language of creation, its nature is to reveal God, and its purpose is to glorify God; it must be desecularized. That is, the patina of secularization with which mathematics has become encrusted must be polished away so that its true, God-reflecting nature shines through. Nearly always, students must have this done for them by their teacher until the idea takes root in their minds. In Christian school vernacular, this process is usually called “integration” of faith and learning. It has been pointed out that the word “integration” implies that two separate entities are somehow mixed or married, which is really not the case. There is just one truth, whether it be in mathematics or elsewhere. “Integration” is more accurately described as “a re-interpretation of data in the perspective of a Christian world view.”3
The Association of Christian Schools International admonishes its conference seminar leaders to give examples of how to integrate, and to deemphasize the fact that we should integrate, on which everyone agrees. Searching for a flickering candle of how to in the vast, dark, foreboding forest of we should, is a task which bears down heavily upon every conscientious Christian school teacher. Especially is this true in mathematics, which has been called “the hardest subject to integrate.” Mathematics has acquired this reputation because its content is the same, no matter who is teaching or what name is painted on the front of the school. No “reinterpretation of data” is possible, which leads Christian mathematicians to the conclusion that “God’s revelation is silent” in mathematics. There are no value judgments or personalities to explore, nothing to preach about.
In other subjects, differences of opinion regarding the nature of the discipline lead to differences regarding its content, value, and application. The varied value judgments inherent in the content of these studies provide ample grist for the “integration” mill. It is impossible for even the creative teacher to exhaust the rich potential for comparing, contrasting, analyzing, and discussing these differences. For example, what you consider “good” literature affects the content of your English course. Even in science, your choice of topics will be influenced by your views of the origin of the universe.
What you think about the nature of man, and your assumptions concerning randomness and chance, determine your perception of what should be included in the content of historical studies. Yankees attending history classes in southern schools begin to wonder who won the Civil War. In some countries, young people graduate without even knowing there was a Civil War. Yet, given the topic, mathematics courses are the same, worldwide.
So the Christian mathematics teacher, listening to his colleagues in social studies describe eloquently the contrasts between the Christian and non-Christian view, not only in the nature of the discipline, but also in its content and applications, sometimes wonders if he or she is doing all he or she should be doing in “integrating” mathematics. Such a teacher is not satisfied with the outlook of the head of the mathematics department of a major West Coast Christian university, who told a group of Christian teacher conferees, “About all you can do is explain to your students that while mathematics is a tribute to our human intellect, God is the one who gave us our minds.” He then gave them the “Kronecker cliche” I quoted earlier.
Small wonder that the mathematics major featured in a magazine advertisement for this institution unwittingly testified to the dichotomous worldview he received there. The text of the ad:
Basically I’m a problem solver. I learned a lot about problem solving as a math major at ————. Algebra, Geometry, Calculus. They might not sound very exciting, but those classes taught me how to attack and solve problems quickly, logically. Having Christian professors really made a difference. [You can almost hear him add, “too.”] By their teaching I learned professional skills. By their example I learned about Christian living. Practical instruction. Techniques for problem solving. Christian principles for my life. I’m using them all today—thanks to —.
The implication is that mathematics has no spiritual value and is useful only for “professional skills.” The Christian air he breathed in the university’s classrooms constituted the spiritual “side” of his education. Scanning the catalogs of most Christian colleges produces not even a hint that God has anything to do with mathematics.
The following is from a Christian college brochure given out at an ACSI convention.
The Bachelor of Arts degree in Mathematics is designed to provide a practical application of mathematical principles to a professional career such as statistics, research work, computer programming or teaching. It would also fit the needs of the student who wishes to continue in graduate school in mathematics. The curriculum for the mathematics major pursuing a Bachelor of Science degree is designed to help the student develop a practical outlook so that he will be able to pursue a future in applied mathematics such as: industrial mathematical programming, marketing, insurance statistics and finances. Students considering this major should be aware that some companies prefer to hire employees with a mathematics background because mathematics majors have a good scientific vocabulary and they enjoy solving problems.
A final example, also from a brochure acquired at an ACSI convention, is entitled: “Purpose of the mathematics department of ———— College.”
- The Mathematics Department is structured to support the departments of Geo-science, Biological Science, Teacher Training and Home Economics.
- This course of study is designed to prepare students to teach mathematics at the secondary school level.
- Each course is well founded in mathematical theory, but tempered with good practical applications to prepare the student to meet the complexities of our society which is becoming more specialized with each passing day.
- The mathematics program is designed to develop the skill of logical thought. The student will learn to identify the problem, isolate, and process its component parts in a proper order and arrive at a correct conclusion.
Even if I discount the mass of evidence indicating that “training-the-brain-to-transfer-knowledge” is a fallacy, I am still nonplussed to find Christians devoting their lives to the study, research, and teaching of a discipline which, as far as they are concerned, has nothing to do with God, and is profitable only for the merchandise its practitioners can make of it. Through some chink in logic, mathematics escapes from the set of all their thoughts, which the Bible says is to be “brought into captivity to Jesus Christ.”
I tend to agree with Harold Lindsell’s evaluation of evangelical colleges:
Numbers of their faculty members have taken doctoral work in the hard and soft sciences without an awareness that what they have learned in secular universities has implications for their Christian faith. Numbers of these professors teach one thing in the classroom, and believe something else in church on Sunday morning. They have never put two and two together. Many of them have no awareness that there is a dichotomy between what they believe in their hearts and what they teach from their heads. But almost inevitably they have been conditioned in such a way that the so-called “certainties” of their doctoral disciplines cause them to test Scripture against these “certainties” rather than testing their presuppositions and conclusions against biblical revelation.4
It is true that the content of mathematics is the same for atheist or Christian. It is also true that this could mean God has nothing to say in mathematics. I have tried to show that the consequences of this assumption do not square with things as they really are. Another perfectly logical explanation for the universality of mathematics content is that it is all God’s; this is the realistic position.
If mathematics is an entity which always exists in God’s mind, it would be in no way affected by the Fall. Since man is affected, his perception of the mathematics revealed in creation no doubt is distorted and is definitely incomplete. Nevertheless, there is universal agreement on the content defining mathematics.
If you grant the existence of the “infinite-personal God-who-is-there,”5 this consensus, existing in no other discipline, can be explained only by acknowledging the mathematics perceived by man to be nearly identical with the mathematics revealed by God in creation. Otherwise God has perpetrated a massive hoax, an action which is not in His character. “God is subtle,” Einstein said, “but not malicious.”6 An interesting comment on this idea is given in Revelation 21:17, which states that measurements used by humans are the same as those used by the angels.
Students must learn that the internal coherence and natural applications of mathematics preclude the rationality of assuming its origin is humanistic.
The field of dispute is the nature of mathematics, and it is on this field that the Christian teacher must focus his or her “integration” effort. The students must learn that the internal coherence and natural applications of mathematics preclude the rationality of assuming its origin is humanistic. Little or no reinterpretation of mathematics content needs to be done; given the truth about its foundation, the student comes to realize that he or she is “thinking God’s thought after Him” when he or she does mathematics. The spiritual vision of the student gradually is renewed to perceive the “eternal power and Godhead” of the Creator, blazing away at the core of mathematics and, in glorious spectra, reflected from every facet of the discipline.
It is true that the melody of nature’s song can be enjoyed without knowledge of its underlying mathematical structure. If you are privileged to view the creation through a microscope or a telescope, to hear the sound of wind or thunder, to hold a baby duck or a baby person, you come to appreciate the beauty and power in nature7 whether you are acquainted with “The Mean Value Theorem” or not. But the lyric of “the music of the spheres” is clearly mathematics, a knowledge of which unveils not only vistas of beauty and power unsuspected before, but also an order, symmetry, and infinitude which stuns and awes the beholder.
Beauty, power, order, symmetry, infinitude—though these characteristics of mathematics are there for anyone, the Christian sees them in their proper light as reflections of God’s attributes. So there is something to be done with content, after all; the teacher periodically identifies these qualities for the students and reminds them that what they are beholding are beams of God’s glory.
A misconception soon arises, one so common in Christian circles that it ensnared even the great mathematician Leonhard Euler. For Euler, the equation (a + bn) / n = x was sufficient proof that “God exists after all.”8 It is to be expected that, in their enthusiasm, students begin to think they have proved that God is the source of mathematics. They need to be shown their starting point—the assumption that God exists—from which they expect to see intimations of His glory reflected from mathematics. Their expectations are realized. And it feels almost as good to find that one’s presuppositions have realistic consequences as it does for one to “prove” something. Euler corrected, would affirm, “God exists, therefore (a + bn) / n = x.”
Lest they feel shame at beginning with faith, students need reminders that the only people not operating from an initial faith base are those populating the various cemeteries of the world. Humans believe, then understand, not the other way around. So, while authors like Lancelot Hogben are wrong to imply that mathematics is without spiritual significance, they correctly deride the stupidity of using mathematics to “prove” “Pope Leo X was the Beast of the Apocalypse”9 or “the creation of the world out of nothing by divine providence.”10
Christians had loaded Euclidean geometry with a burden it was never meant to bear, practically making the existence of God contingent upon the “self-evident truths” of geometry.
Cart-pull-horse thinking was also what precipitated the devastating blow to faith when the non-Euclidean geometries were discovered. Christians had loaded Euclidean geometry with a burden it was never meant to bear, practically making the existence of God contingent upon the “self-evident truths” of geometry.
Davis and Hersh cite two other “stunning surprises”—the discovery of space filling curves, and continuous, nowhere-differentiable curves—which
exposed the vulnerability of the one solid foundation—geometrical intuition—on which mathematics had been thought to rest. The loss of certainty in geometry was philosophically intolerable, because it implied the loss of all certainty in human knowledge. Geometry had served, from the time of Plato, as the supreme exemplar of the possibility of certainty in human knowledge.11
I reiterate that this loss of certainty was an apparent loss only. The non-Euclidean geometries, quaternions, and the maverick curves mentioned by Davis and Hersh were like pieces of a jigsaw puzzle which we put to one side until the puzzle “catches up” to them. And catch up it did.
The Christian teacher, rightly beginning with the assumption that mathematics originates with God and consequently possesses a nature which reflects His glory, has the freedom and responsibility to point out the evidence of God’s hand in the content of mathematics. For example, the idea of sets is one of the great unifying strands in mathematics, and infinite sets reflect dramatically the infinitude of the Creator.
Specifically, the teacher directs the students’ attention to the interval on the number line between 0 and .00001. This interval has a midpoint x1, the segment between 0 and x1 has a midpoint x2, and so on. These xi’s form an infinite set, but are only a “few” of the rational numbers between 0 and .00001. Even if all of the rational numbers in this interval could be labeled, there would remain infinitely many irrationals also residing there, filling the “holes” between the rationals. And this segment which contains these infinitudes of infinite sets is only a microscopic snip of a number line which itself stretches to infinity. When you attempt to get your mind around the stunning myriad of numbers God has given us, you come afresh to the realization that there is “more than man” in mathematics.
Georg Cantor’s ingenious arrangement of the rational numbers given below brings an appreciation of what “infinite” means, but some of the effect is lost because the set is not bounded above.
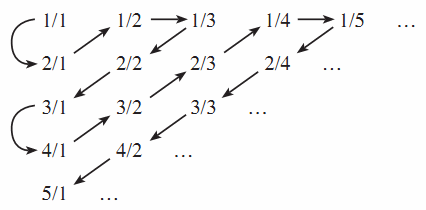
However, when you study integration as the area under a curve, you get a dynamic, almost cinematic display of the rectangles in a closed region becoming smaller and more numerous; you can almost “see” the ultimate saturation of the area occur, when there are infinitely many rectangles. An even greater awareness of the meaning of infinity grows when you derive the actual integration formulas for elementary functions, using summation and limit theorems and the principle of mathematical induction. The reflected infinitude of the Creator is nowhere more evident on earth.
When you solve a system of equations or inequalities, you behold the power of God Who designed a process which efficiently sifts through infinite sets and quickly finds solutions, or indicates that none exist. Major chores in algebra are factoring, canceling, and combining. What have these to do with God? Used to simplify expressions, these processes are like editing a manuscript, except that the rules for editing mathematics are precise. Students are reminded that mathematics is the language of the creation; they edit it to get as close as possible to His original word. As I have shown previously, mathematicians acknowledge that there is one “best” way.
The pressures of How To “integrate” force some Christian teachers to the object lesson approach. The biblical utilization of object lessons demonstrates their general usefulness, but we must realize that, since the object is never the lesson, this method can not be used to desecularize a subject. The object is the takeoff point or illustration of the lesson, but they remain separate entities. So, when mathematics is used to illustrate biblical truth, nothing is learned about the relation of mathematics to God, which was the teacher’s purpose in the first place. In such an approach, the dichotomy between secular and spiritual which exists in the teacher’s mind is emphasized, rather than healed by a supposed “integration.”
Some examples of object lessons which have been used in Christian school mathematics classes are:
- Vectors
- Christians need more than just magnitude, they also need a direction in their lives.
- Substitution Property
- Christ’s death for us.
- Common Factor
- In Christians, Jesus Christ.
- One-to-One Correspondence
- Christ has a unique place for each Christian.
- Absolute Value
- God has absolute values which can’t be changed just because of situations.
Although the “lesson” uses the same word which names the mathematical “object,” it is obvious that a completely different meaning is imputed. No “integration” has been achieved.
Persons who couch the expression of problems, definitions, or theorems in what Schaeffer calls “God-words” are likewise not “integrating.” Here is an example:
To illustrate how negative and positive signs affect the quotient of two integers, let “+” represent the clause, “it is true” as well as the true statement “Christ lives.” Then let “–” represent the clause “it is false” as well as the false statement “Christ never lived.” The operation of division can be represented by the word “that”. Carefully study the combinations of clauses and statements as well as the conclusions that follow:
| A. It is true that Christ lives. | This is a true statement. | |
| + ÷ + | = | + |
| B. It is false that Christ lives. | This is a false statement. | |
| – ÷ + | = | – |
| C. It is true that Christ never lived. | This is a false statement. | |
| + ÷ – | = | – |
| D. It is false that Christ never lived. | This is a true statement. | |
| – ÷ – | = | + |
The inference could be made that a teacher using this approach does not really believe that the rule of signs for division has anything to do with God, and is attempting to remedy the deficiency. I was at an ACSI workshop and was disappointed (horrified?) to hear the following being used as an example of “integrating mathematics.”
Natural Law: 4+4=8.
God’s Law: Murder leads to punishment.
Conclusion: Just as 4+4=8, so murder leads to punishment.
What appears to be “integrating” is actually dichotomizing. True desecularization involves the actual substance of mathematics, what is really there, intrinsic to the subject. Since it is God’s thinking, it must itself reveal Him.
Truth & the Transcendent
“How do you know that God created mathematics?”
Read OnlineFootnotes
- The Sorrow and the Pity, A film by Marcel Ophuls, (New York: Outerbridge and Lazard, 1972), pp. 9, 11.
- Mark Fakkema, Christian Philosophy and its Educational Implications, BK. 3, (Chicago: National Association of Christian Schools), p. 76-T.
- Ronald L. Kotesky, “Man in Christian Psychology,” Christian Association For Psychological Studies, Proceedings (Grand Rapids, 1974), p. 14.
- Harold Lindsell, The Battle for the Bible (Grand Rapids: Zondervan, 1978), p. 183.
- See Schaeffer, Escape from Reason, or any others of his books.
- Inscription over the faculty lounge fireplace, in Jones Hall, Princeton University.
- See “The Price for Praise” by Virginia Stem Owens, Christianity Today, 18 Nov. 1977, pp. 14–16; or poetry of Gerard Manley Hopkins.
- Lancelot Hogben, Mathematics for the Millions, 3rd ed., (New York: Norton, 1962), p. 17.
- Hogben, 478.
- Hogben, 486.
- Davis and Hersh, 331.
Recommended Resources

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- © 2024 Answers in Genesis





