How Big Is the Universe?

Introduction

How big is the universe? The universe appears to be very large — billions of light-years across. Since this is far larger than a few thousand light-years, people frequently ask how we can see objects this far away if the universe is only thousands of years old, as the Bible seems to imply. This is a very good question — so good that we have given this question a name: the light travel time problem. There are a number of proposed solutions to this problem, but I will not discuss those here.1 Instead, I will address the question of whether the universe really is as big as is often claimed. The short answer is, yes, the universe most certainly is that large. To explain this conclusion, I will describe some of the methods astronomers use to measure distances of astronomical bodies.

I emphasize that there are three realms of astronomical distances: those within the solar system, those within the galaxy, and those of objects outside of our galaxy. The techniques used in these realms are different, and there is little overlap between the techniques used in those realms. The first distance measurements in astronomy were within the solar system, and they were done by geometric means as planets orbited the sun. This largely was replaced by more accurate radar measurements in the latter half of the 20th century. I will not discuss solar system distances, for the light travel times involved here amount to mere hours at most, and thus are not a problem for recent creation. The sun and all the stars that we can see are members of the Milky Way galaxy, a vast collection of more than 100 billion stars spanning nearly 100,000 light-years. The term “stellar distance” normally refers to measuring distances of stars within the galaxy. The first stellar distance measurement was in 1838. There are billions of many other galaxies, each of them being millions or even billions of light-years away. We say that the distances of other galaxies are extra-galactic. The first extra-galactic distance measurement was in 1924.

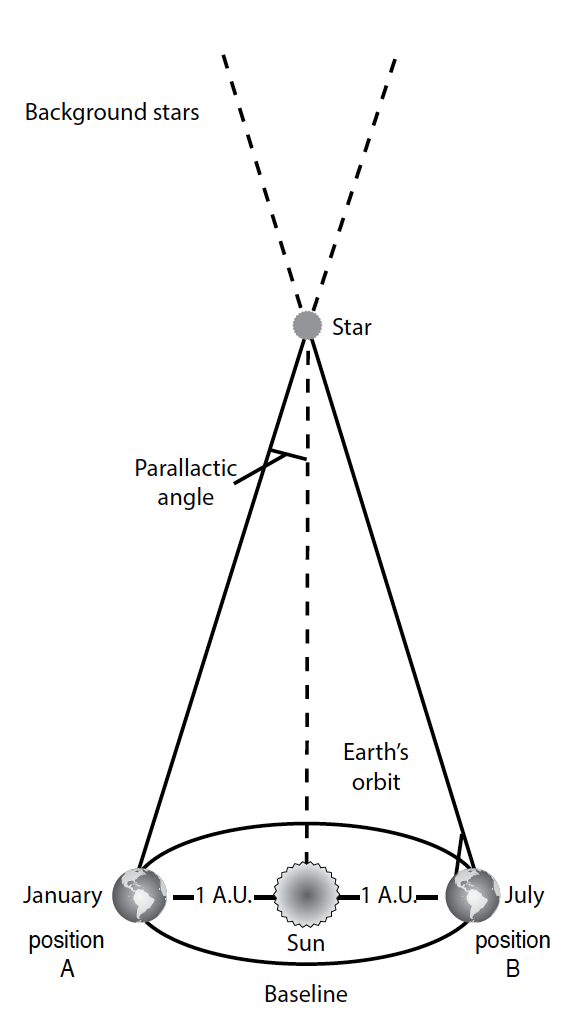
Figure 1

The first stellar distance measure used trigonometric parallax. Trigonometric parallax employs the principle of the apparent shifting position of an object due to our changing location from where we view the object. You can illustrate this by looking at your upheld thumb at arm’s length. Close one eye and note the position of your thumb with respect to background objects. Now open that eye and close the other eye. You’ll notice that your thumb appears to shift position. We call this apparent shift in position parallax. If you hold your thumb closer to your eyes or if you try this with a more distant object, you will discover that the amount of parallax depends upon the distance of the object — the greater the distance, the less the parallax. The amount of parallax also depends upon the length of the baseline, in this case the distance between your eyes. For a given distance, a greater baseline produces a larger parallax. Surveyors have long used this technique to measure the distances of faraway objects and altitudes of mountains. They set up a transit (in ancient times a dioptra) to view a distant object and measure the angles that the object made at either end of the baseline. Using the baseline and angles, one can use simple trigonometry to measure the distance to the object.

In similar manner, astronomers use the baseline of the earth’s orbit around the sun to measure the apparent shift in the positions of nearby stars with respect to more distant stars. An astronomer at location A on one side of the earth’s orbit measures the position of a star. Six months later, when the astronomer has arrived at position B on the other side of the earth’s orbit, he re-measures the position of the star. The total shift in apparent position is a very small angle, so we normally express it in seconds of arc.2 Notice that the baseline is the diameter of the earth’s orbit, which is twice the distance of the earth from the sun. The average distance of the earth from the sun is a standard unit of distance that astronomers call the astronomical unit (AU for short). Astronomers express the baseline as one AU, so the parallax angle is defined to be one-half the total measured shift. The closest star, Proxima Centauri, has the largest parallax, but its parallax is less than one arc second. And its distance is about 26 trillion miles, so use of normal trigonometric relationships would be quite cumbersome. To avoid this and use a very simple formula, astronomers have defined their own units. If d is the distance of the star and π is the parallax, then the formula is:

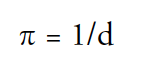
Note that π here is a variable and does not refer to the ratio of the circumference of a circle to its diameter. For this equation to work, astronomers have defined a new unit of distance, the parsec (abbreviated pc). The parsec is the distance that a star would have if its parallax were one second of arc.3 Since we normally measure the parallax and then compute the distance, we can re-write the equation:

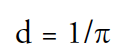
Friedrich Bessel was the first to measure a star’s parallax in 1838 (the star was 61 Cygni). In the early 20th century, astronomers began to use photography for parallax work. The techniques of the time allowed reasonably accurate measurements of stellar distances (within 20 percent) out to about 20 pc (65 light-years) and thus included a few hundred stars. The primary limitation of this work was the blurring of the earth’s atmosphere. To avoid this problem, the European Space Agency (ESA) launched the Hipparcos satellite in 1989. The Hipparcos mission accurately measured the parallaxes of more than 100,000 stars, providing good distances to about 600 light-years. ESA has scheduled the launch of Gaia, a much-improved mission, in late 2013. If successful, Gaia will accurately measure distances of millions of stars to tens of thousands of light-years. Obviously, parallax data obtained so far are not a problem for recent creation, but the Gaia data could be a problem for a creation that is only 6,000 years old.

Trigonometric parallax is the only direct method of measuring stellar distances, but astronomers have developed other indirect means. Many of these indirect methods involve the use of “standard candles.” A standard candle is a star or other object for which we have a good idea of how bright it actually is. Astronomers use magnitudes to express stellar brightness. A star’s apparent magnitude, m, is how bright a star appears to us. Its absolute magnitude, M, is a measure of how bright a star actually is, defined to be the apparent magnitude a star would have if it were ten pc away. A star’s apparent magnitude depends upon the star’s absolute magnitude and its distance. We can directly measure m, and if we think that we know M, we can form the distance modulus m – M. We can find the distance, d, in pc, by inserting the distance modulus in the following formula:

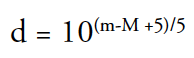
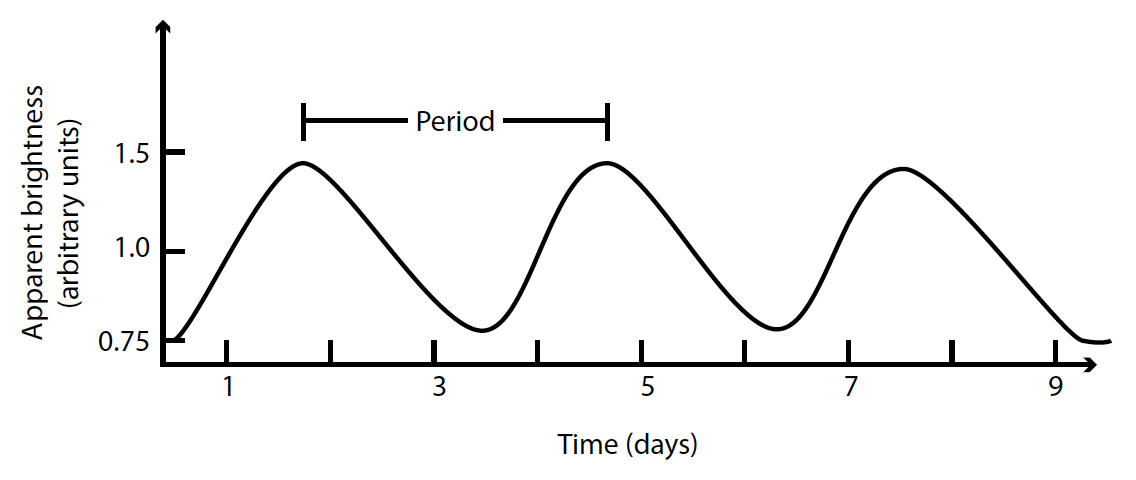
Figure 2. A Cepheid variable light curve showing the period

The best example of a standard candle is the use of Cepheid variables. Cepheid variables are pulsating giant and super giant stars with temperatures similar to the sun. As these stars pulsate, their diameters alternately increase and decrease while their temperatures cyclically change. The changes in size and temperature cause a Cepheid regularly to vary in brightness over a definite period. The periods of Cepheid variables range from two days to two months. About a century ago, the astronomer Henrietta Leavitt discovered that Cepheid variables follow a period-luminosity relation. That is, the longest-period Cepheid variables have the greatest average brightness. In observing a Cepheid variable, an astronomer obtains the star’s average m and period. Knowing the period, the period-luminosity relation reveals the Cepheid variable’s absolute magnitude, which yields the distance modulus and hence the distance. Astronomers had used some other indirect methods to calibrate the period-luminosity relation, but now the Hipparcos mission has allowed direct calibration, in good agreement with the indirect methods. How do we know that a particular variable star indeed is a Cepheid? Cepheid variables have unique characteristics, such as their temperature and the shape of their light curves. The physics of the pulsation is well understood, and from the theory we would expect them to follow the period-luminosity relation.

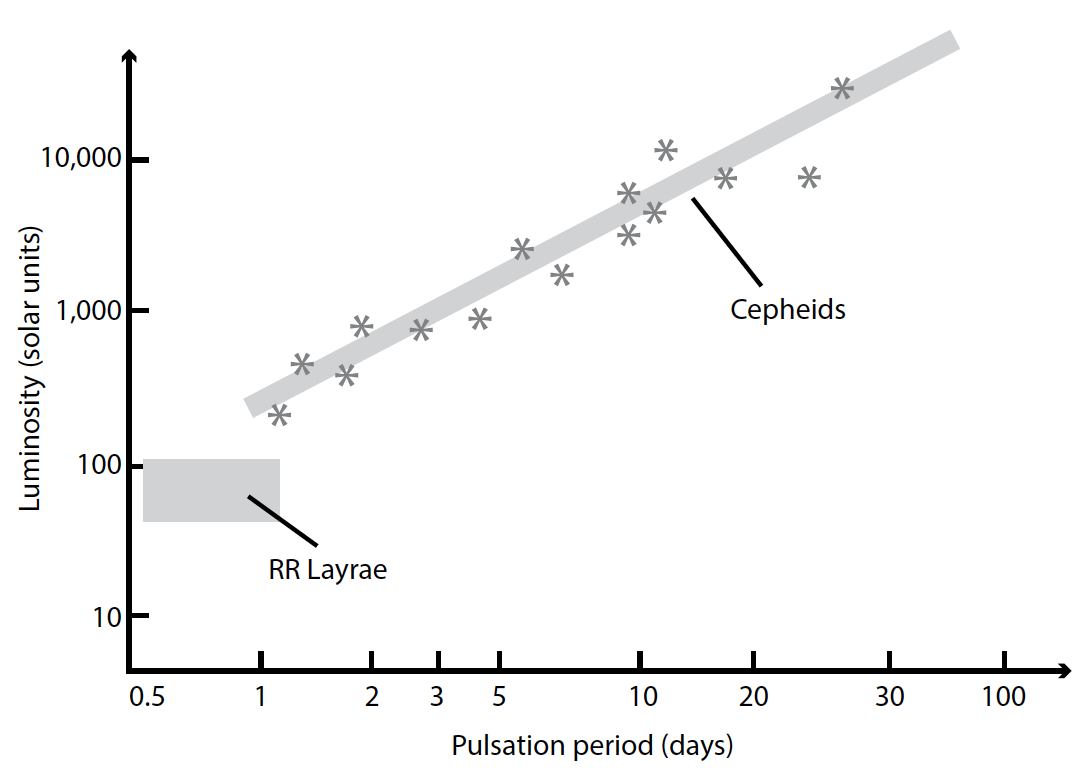
Figure 3. The period-luminosity diagram

In addition to standard candles, astronomers can compute distances of stars by estimating their intrinsic luminosities. The spectra of stars contain dark absorption lines that form in the atmospheres of stars. Absorption lines normally are very narrow, but various mechanisms can broaden spectral lines. One of the most important broadening mechanisms in stellar spectra is pressure broadening. The physics of pressure broadening is well understood, with the result being there is an inverse relationship between the amount of pressure broadening and the size of a star. That is, the largest stars have the narrowest lines. Astronomers can estimate the size of a star (expressed by radius, R) by how broad its spectral lines are. We can also determine a star’s temperature, T, expressed in Kelvin, a number of different ways. The total luminosity, L, of a star may be expressed as:

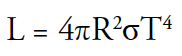
In this equation, σ is the Stefan-Boltzmann constant. When combined with a model atmosphere, we can convert the luminosity to an absolute magnitude. If we measure the star’s apparent magnitude, we know the distance modulus, and we can use the previous equation to find the distance of the star.

Figure 4. Crab Nebula
(Shutterstock.com)

There are some specialized distance determination methods. A good example of this is use of the expansion rate of the Crab Nebula to find its distance. The Crab Nebula is the remnant of a supernova that the Chinese recorded seeing on July 4, 1054. Modern photographs taken a few decades apart reveal that knots of material near the periphery of the remnant are moving outward. Measurement of the motion of those knots allows astronomers to estimate the age of the remnant, an age consistent with the known age. In addition, emission lines in the spectrum of the remnant have both positive and negative Doppler motions along our line of sight. The negative Doppler motion comes from gas moving toward us on the near side of the remnant, while the positive Doppler motion comes from gas on the far side moving away from us. We combine this Doppler motion with the aforementioned expansion of the knots to measure the size and distance of the Crab Nebula. This last step assumes that the expansion is uniform in all directions. The nebula is elongated on photographs, showing that the expansion is not exactly uniform, but this simple assumption probably introduced less than 25 percent error in the final results. We find that the Crab Nebula is about 6,000 light-years away.

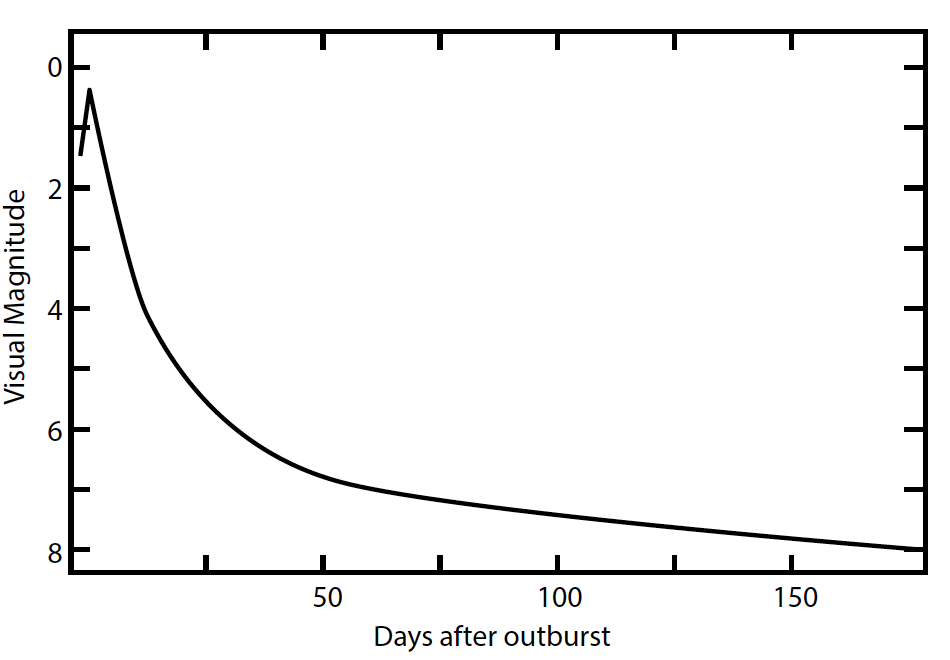
Figure 5. A nova light curve

It is most fortunate that the Crab Nebula also contains a pulsar. Pulsars are radio sources that periodically flash radiation with very regular periods. Astronomers think that pulsars are rapidly spinning neutron stars. There are now more than 2,000 known pulsars, with periods ranging from about a thousandth of a second to a few seconds. Pulsar timings are done in the radio spectrum, and astronomers have found that the pulses are slightly delayed, or dispersed, depending upon the frequency of observation. Dispersion is a well-understood phenomenon, and in addition to dispersion depending upon the frequency, dispersion also depends upon the number density of electrons, n, in the interstellar medium (ISM). The dispersion of the Crab Pulsar and its known distance allow astronomers to measure the average value of n in the ISM along our line of sight to the Crab Nebula. Given the great distance of the Crab Nebula, this appears to be a good average of n in the ISM, which in turn allows radio astronomers to measure the distance of any pulsar with dispersion measurements. This has been done with nearly all pulsars. One of the closest is PSR J0108-1431, about 400 light-years away. Pulsars are found throughout the galaxy, with distances up to tens of thousands of light-years. Furthermore, astronomers have found pulsars in the Large and Small Magellanic Clouds, two small satellite galaxies of the Milky Way, about 160,000 and 200,000 light-years away.

The various methods of finding distances within the Milky Way galaxy help establish the size of the Milky Way, about 100,000 light-years across. Since these distances are greater than 6,000 light-years, there is some tension between recent creation and these distances. I now turn my attention to extra-galactic distances. Since Cepheid variables are such bright stars, we see them in other galaxies, so this is the one overlap between these realms. The only difference between galactic Cepheids and extra-galactic Cepheid variables is that the ones in other galaxies are much fainter than the ones that we see in our own galaxy. It follows from their faint apparent magnitudes that these Cepheid variables, and hence their host galaxies, are millions of light-years away.

Milky Way over the desert of Bardenas, Spain
(Shutterstock.com)

In addition to Cepheid variables, astronomers have developed other standard candles for extra-galactic use. They include:

1. Novae
2. Bright super giant stars
3. Bright Globular star clusters
4. Bright HII regions
5. Type Ia supernovae

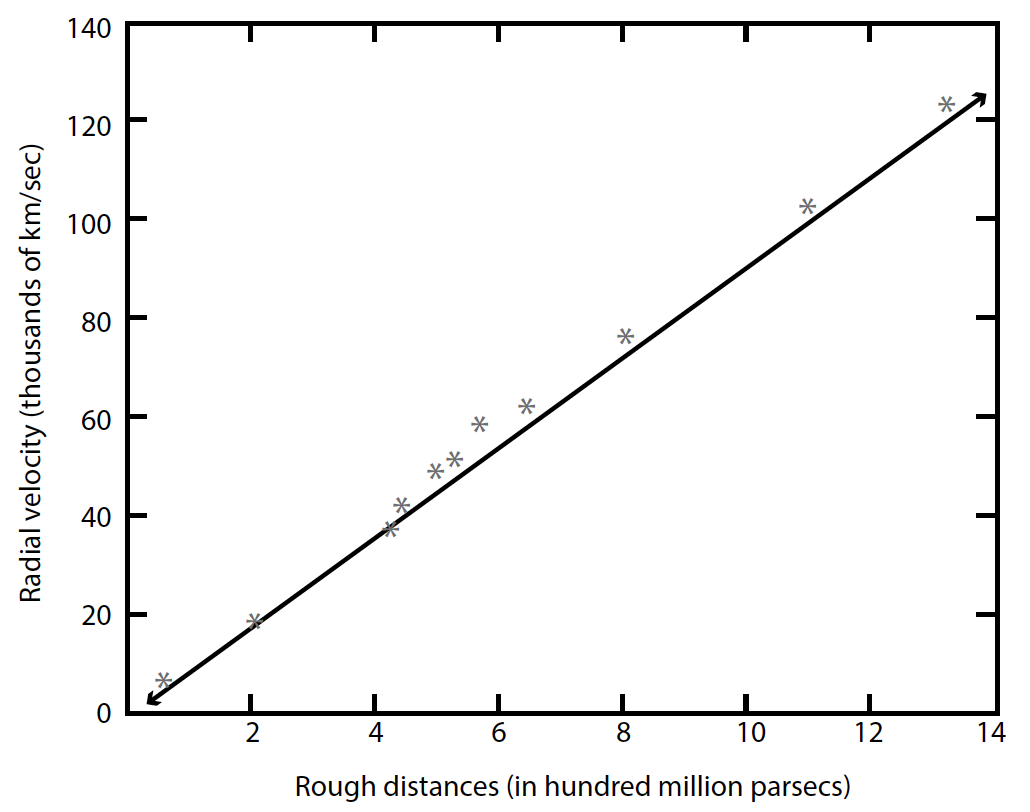
Figure 7. Hubble relation

Novae are eruptions on white dwarf stars in close binary systems, and they have a large range in brightness. But the brightest, classical novae appear to have a narrow range in maximum absolute magnitude. If we happen to observe a nova in another galaxy near its peak brightness, we can measure the apparent magnitude, find the distance modulus, and use the distance formula to find the distance. In similar manner, it appears that the brightest super giant stars in galaxies of the same type have about the same absolute magnitude, allowing an estimate of distances. Large spiral galaxies like the Milky Way have about 200 globular star clusters. The largest and brightest have about the same absolute magnitude. In addition, globular clusters have some appreciable diameter, so that they show up as extended objects on photographs. The largest globular clusters have about the same diameter, so their apparent size can be used as a method of finding distances to them and hence their host galaxies. HII regions are glowing clouds of ionized hydrogen gas surrounding hot, bright stars. While HII regions vary in size and brightness, like globular clusters, there appears to be uniformity among the biggest and brightest ones. These methods now work out to a distance of nearly 50 million light-years. Within this range, astronomers like to use several methods and average the results. The variance gives an idea of the errors involved.

Figure 8. Globular cluster
(Shutterstock.com)

Type Ia supernovae characteristics are distinctive from other types of supernovae, so they are easy to identify. In recent years, they have stood out as one of the most powerful methods of finding extra-galactic distances. Astronomers think that a type Ia supernova results from the disintegration of a white dwarf star in a close binary system. The white dwarfs involved in this scenario are so similar that the resulting explosions are nearly identical. This means that at peak brightness all type Ia supernova have the same absolute magnitude, so measurement of the apparent magnitude easily yields the distance. Supernovae are rare events in any particular galaxy, but in recent years astronomers have automated robotic telescopes to look for type Ia supernovae in other galaxies.These robotic telescops have discovered a vast number of these supernovae and hence distances to the host galaxies. In 2013, the HST detected a type Ia supernova about ten billion light-years away. In 1999, data from type Ia supernovae played a key role showing that the rate of expansion in the universe may be speeding up, an effect attributed to dark energy. The only restriction on this method is that it works only for galaxies that have type Ia supernova that we happen to observe.

Finally, since Edwin Hubble’s 1928 discovery of the expansion of the universe, astronomers have used the Hubble relation to find the distances of galaxies. Redshift is a measure of how much the lines in the spectrum of a galaxy are shifted toward longer (more red) wavelengths.4 Hubble showed that there is a relationship between redshift and distance, something that one would expect if the universe is expanding. There is some scatter in the data, but the trend generally holds. Mathematically, we can represent the Hubble relation as:

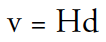
In this equation, v is redshift expressed as velocity in km/s, d is the distance in Mpc (megaparsec = one million pc), and H is the Hubble constant. This is the equation of a line with H being the slope. H is difficult to determine, but once we get that, we can find distances by re-writing the Hubble relation:

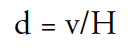
As long as there is enough light to obtain a spectrum of a galaxy, we can measure the galaxy’s redshift, and we may use the Hubble relation to find its distance.

Conclusion: How Big is the Universe

I have described here some of the simpler and more often used methods of finding distances to galaxies. In each case, they produce distances that are millions and even billions of light-years. While all of these methods suffer from error, those errors would not reduce the distances down to just thousands of light-years. The universe is very large, much larger than people can really comprehend. Douglas Adams probably said it best in The Hitchhiker’s Guide to the Galaxy:

You just won’t believe how vastly hugely mind-bogglingly big it is. I mean, you may think it’s a long way down the road to the chemist, but that’s just peanuts to space.5

Many recent creationists worry about the light travel time problem and entertain possibilities of the universe being far smaller than generally thought as a way out of this dilemma. But thinking this stumbles over something that ought to be obvious. Only a truly powerful Creator could conceive and make such a large universe. It is as if He created the world so large that we finite creatures upon seeing His handiwork ought to fall down prostrate in worship of Him. It may not be possible for a mere human to truly grasp the immensity of the universe, and understanding the power required to create such a universe is infinitely beyond that, but we creationists accept that fact. Yet we so often stumble over how God could have brought the light here so that we could see the universe. Compared to creation, the light travel time problem is trivial. Chapter 21 briefly discusses some of the proposed solutions to the light travel time problem.