
Distant Starlight and Genesis: Conventions of Time Measurement
Originally published in Journal of Creation 15, no 1 (April 2001): 80-85.
Abstract
There are two useful conventions to define the time an event occurs: calculated time and observed time.
Summary
Although calculated time has become the standard convention, it may not be the convention used in Scripture. This paper serves not to introduce any new astrophysical ideas, but rather to clear up a common misconception—a mismatch of conventions of measurement. Once this misunderstanding is eliminated, it becomes obvious that distant starlight does not prove that the universe is billions of years old, and neither is it a legitimate argument against the Genesis account of Creation.
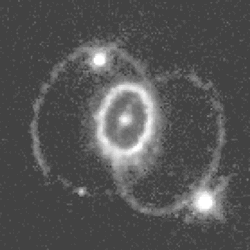
In 1987, astronomers discovered a new point of light on an image of the Large Magellanic Cloud. This was a supernova—an exploding star—and was given the name ‘1987A’ (Figure 1). If someone were to ask a professional astronomer when this event occurred, the astronomer might reply, ‘It occurred in 1987 of course’. But the person would explain, ‘No, I mean when did it really happen?’ To this the astronomer would say, ‘Oh, about 200,000 years ago’. By this, the astronomer means that the supernova is so incredibly far away, that its light must have left 200,000 years ago to reach Earth in 1987. Light travels at the incredible velocity of 1,079 million km/hr. This is why it is able to travel from the supernova to Earth in ‘only’ 200,000 years.
So, when dealing with the time of an astronomical event, there are two logical questions: ‘When did we see it happen?’ and ‘When did it really happen?’ The first is an observational question. It can be answered by looking at a clock when the event occurs. The second question requires a simple mathematical operation: the distance to the object is divided by the speed of light, and this quantity is subtracted from the time the event was observed. Both questions ask a specific, quantifiable question regarding the time of the event. Therefore, we see that there are two possible definitions of time. We shall call the first ‘observed time’, in which the time of an event is described as when we see the event occur. The second definition we call ‘calculated time’, in which the time of an event is calculated by subtracting the light travel-time (distance to the event divided by the speed of light) from the observed time. Calculated time is usually considered the ‘true’ time.
This immediately presents an apparent problem for Biblical creationists. The Bible states in the first chapter of Genesis that God made the stars on Day 4 of Creation Week. A straightforward reading of Scripture shows that Creation must have happened about 6,000 years ago. This means that the light from distant stars should not yet have reached the Earth. Yet clearly it has, because we do see very distant stars. This is no small problem, for we are able to observe galaxies of stars that are so far away that their light should have taken billions of years to reach Earth. Some people claim that this disproves the Genesis account of Creation, and proves that the universe is billions of years old, not thousands.
Previous attempts at reconciliation
Christians have had difficulty reconciling these ideas with Scripture. Many explanations have been proposed, but none of them prove completely satisfactory. Some have claimed that the days in Genesis were not literal 24-hour days but could have been long periods of time, but this is not warranted by the context. Others have claimed that God created the light en route, but this would mean that supernova 1987A never actually happened, but rather that God created the image of the exploding star en route to Earth. Moreover, it would mean that the progenitor star never actually existed even though we have been able to see its image throughout time. While some ‘appearance of age’ is essential in a supernaturally created universe where things were created functionally mature, would God create the image of a star that never actually existed, or a supernova that never happened? Perhaps we cannot completely eliminate this possibility, but it nonetheless seems a remarkably uncharacteristic act for the God of the Bible.
Some have claimed that light may have travelled faster in the past. This idea is intriguing, but the speed of light is not an arbitrary ‘free’ parameter. A change in the speed of light would have profound consequences for the rest of physics, and these are not observed. Others have proposed that gravitational time-dilation may cause different parts of the universe to age at different rates (so the universe really could be billions of years old from some points of view, but only thousands of years old as measured by an observer on Earth).1 This theory is ingenious, and the premise is sound. But the model may have fatal quantitative problems, and may fail to produce the degree of time-dilation required for starlight billions of light years away to reach Earth in 6,000 years.
Perhaps the answer is much simpler. Perhaps the definition of time that God uses in Genesis 1 is observed time, not calculated time. In other words, had there been an observer standing on Earth on Day 4 of the Creation Week, he or she would have seen the stars being created on that day. This is certainly the impression we get from a straightforward reading of Genesis. The insightful reader will at this point realize that this view implies that the stars observed on Day 4 were ‘actually’ created years—even billions of years—before Day 1, according to calculated time. This view suggests that God created stars ‘before’ the beginning of time (if such an idea is meaningful) in such a way that their light would reach Earth on Day 4. This idea will be addressed in detail later.
Defining time
It is possible to define a variable t which records when we detect a given event. If t is a legitimate time coordinate (if observed time is ‘real’), then events happen when we see them happen. In this view, light travels instantaneously from stars to Earth (though light travels at different speeds in other directions). But keep in mind that this is due to the way in which we have defined time, not the way that light ‘actually’ travels. If the reader is comfortable with this idea, he or she may skip to the section entitled ‘The Biblical convention’. In the next four sections we will explore the properties of light propagation as measured in observed time rather than the more standard calculated time. I will attempt to show that the unidirectional speed of light is not a unique quantity, but depends on the convention of synchronization chosen by the observer. The following four sections argue that observed time is a fundamentally true—not just phenomenological—language of appearance. This argument is not essential to solve the starlight problem, though it strengthens points made in the last sections of the paper.
Relativity and time
First, we must understand that the measure of time is not the rigid, objective quantity most people think it is. Einstein’s well-tested theory of Special Relativity shows that the motion of the observer affects the measurement of time. Suppose that as an observer on Earth was watching Supernova 1987A explode, a spaceship was flying by Earth at very high speed, with a clock that was (instantaneously) synchronized with a clock on Earth. Both the pilot in the spaceship and the observer on Earth would observe the light from the supernova at the same time. But, they would disagree on when the supernova actually exploded (according to the calculated time). We ask, ‘Who is correct—the observer on Earth or the pilot of the ship?’ The answer is: they both are! Each is correct according to his or her reference frame. (Moreover, each observer could compute the time the other observer would measure if they knew their relative velocity.) This may seem bizarre to those unfamiliar with Relativity, but it is a well-tested principle of nature. A complete discussion of the implications of Special Relativity is beyond the scope of this paper, but many good introductory books have been written on Special Relativity.2
Implications of observed time
Using the calculated time definition, the speed of light in vacuum is constant. It is found to be 1,079 million km/hr in all directions regardless of the velocity of the observer. (This is really a property of spacetime, and the way we have chosen to measure time more than some peculiar property of the light.)
However, using the observational definition of time, the speed of light depends on its direction of propagation relative to the observer. (Again, this is a property of spacetime, and not a property of light. All relativistic particles such as neutrinos would also move at different speeds in different directions.) Light travels at the canonical speed of 1,079 million km/hr only when moving tangentially relative to an observer. It moves at half the canonical value when moving directly away from the observer, and it moves infinitely fast when travelling directly toward the observer—travelling instantaneously from point A to point B.3
This last implication is easy to understand. If we see the supernova exactly when it ‘really’ happens, then the light must have taken no time at all to traverse the intervening space—its speed must be infinite. It may seem bizarre that light should travel at a speed depending on its angle relative to an observer. But is this any stranger than the canonical idea of light being constant regardless of the motion of the observer? Either way, light seems to ‘know’ how the observer is moving and adjusts accordingly. We ask the question, ‘Which definition of time is correct?’ If calculated time is the ‘correct’ definition, then light travels at the same speed in all directions. If observed time is ‘correct,’ light travels at different speeds in different directions. It seems that it should be possible to determine which definition of time best describes when an event ‘really’ happens by measuring the speed of light.
Which is correct?
We now consider an experiment to measure the speed of light to help us determine which measurement of time is correct. We construct a long hallway with a mirror at one end. We stand at the other end and send a light pulse down the hallway at a given time. The light beam propagates down the hallway, strikes the mirror and is reflected back. We subtract the time of departure from the arrival time. We then divide the total distance (twice the length of the hallway) by the total time to obtain the average velocity of light = c. Normally, it is assumed that light travels at the same speed in both directions (isotropic propagation). What if, instead, light travelled anisotropically? What if the light travelled at 0.5 c down the hallway, and infinitely fast back? We would get exactly the same answer. There is no way to tell (from this experiment) if the speed of light is isotropic, or anisotropic.
We try another experiment. This time we will have a clock at both ends of the hallway. We will send the light pulse when the clock at our end reads exactly 12:00. The clock at the end of the hallway is designed to stop when the light hits it. We then read the time. This experiment avoids a return trip altogether, and so should give us the oneway propagation speed. But there is a problem. Before we start this experiment, we must make certain the clocks are synchronized. But how do we do this? We can ‘see’ the time on the other clock, but that is because light has travelled from there to here. How long did it take to do that? There is no way to determine whether or not the clock at the end of the hallway is synchronized with the one at our end without assuming how light propagates. So this experiment must assume the answer to the question being asked and so is of no use to us.
We make one final effort to try to determine the one-way speed of light. This time we have two clocks at our end. We can easily synchronize them since they are both in the same place. We then move one clock to the end of the hallway—knowing that it has already been synchronized. But there is again a problem. Einstein’s Relativity tells us that the time measured by an object is affected by that object’s motion. In other words, the very act of moving the clock down the hall has caused it to become unsynchronized! But perhaps all is not lost. We can calculate how much it is off from our time using Relativity. But there is one fatal flaw: Einstein’s Relativity is normally formulated in calculated time—it assumes that the speed of light is isotropic. Again, we must assume the question we are trying to answer. Although many other one-way experiments can be conceived, they all inevitably make an assumption which nullifies the results. Often the assumption is very subtle and difficult to detect (such as using an equation, which is only valid when light is isotropic4-6).
Conventions of time measurement
There does not appear to be any empirical experiment which can distinguish between isotropic and anisotropic light propagation. Any such experiment would require two time-measuring devices at different locations. There is simply no way to synchronize these clocks without assuming a priori the one-way speed of light. Why is this? It would seem that the question of the one-way speed of light is not fundamentally meaningful. The answer depends on a person’s chosen convention of time measurement. A person can define time such that the speed of light is isotropic and construct an experiment that will confirm this. Another person can define time such that the speed of light is anisotropic—and an experiment will confirm this as well. As long as we are consistent, either definition of time and light propagation is perfectly legitimate—neither is fundamentally the ‘right’ one.
The reason that there is no fundamental way to synchronize two clocks separated by a distance is because the very idea of absolute synchronization is not meaningful in a Relativistic universe. The concept of synchronization is really a vestigial idea from the days of classical (non-relativistic) physics. Synchronization means that two clocks read the same time simultaneously. But, Einstein’s equations show that the concept of simultaneity is a subjective one. (Two observers in different reference frames might disagree about whether two given events happened simultaneously, yet both observers would be ‘correct’.)
Since simultaneity and synchronization are not fundamentally observable, we are free to choose a definition of simultaneity. This means that either observed time or calculated time may be used. It is therefore valid to say that supernova 1987A ‘actually’ happened in 1987, because its light reached us instantaneously as measured by observed time. This may go against our intuition, but from the observed definition of time, it must be true.
Consider the following analogy. We have a one meter long table and we ask: ‘Is this table 100 units long as measured in centimeters, or is it 1,000 units long as measured in millimeters? Which is the correct answer?’ Of course, both answers are correct, the table is both 100 units long, and 1,000 units long depending on the choice of units. Moreover, one unit of measurement is not superior to the other. Both are legitimate, though one may be more useful than the other depending on the circumstances. We can easily convert from one unit to the other, but we cannot arbitrarily interchange the units without converting.7
So the centimeters definition of a unit of length, and the millimeters definition make different predictions about the length of a table. (In other words, it is either 100 or 1,000 units long.) One might try to construct an experiment to find out which definition is ‘right’. Is the table ‘really’ 100 units long or is it ‘really’ 1000 units long? Such an experiment could never work, because the experimenter would have to pick a convention of length (mm or cm) in order to measure the table. Likewise, it seems impossible to empirically determine which definition of time is ‘correct,’ because in any attempt to answer the question one must make a choice of convention.
So we see that clocks are normally synchronized, assuming that light is isotropic (this is called ‘Einstein synchronization’). But the fact that other synchrony conventions are possible is not a new idea. There are many documents on this topic in secular literature.8 In fact, Einstein’s Relativity can be (and has been) formulated using alternate synchrony conventions.9,10 The reader is encouraged to consult the excellent article by Salmon11 on this subject, which offers very clear explanations and debunks several experiments which at first appear to measure the one-way speed of light.
So far we have explored arguments that strongly suggest that synchronization is conventional—not fundamental; and thus, the one-way speed of light is a quantity that is chosen, not measured. However, I caution the reader that not all agree that this is the case.12 The topic is still debated in the literature.13 But even if it could be demonstrated that Einstein synchronization is the only fundamentally ‘correct’ convention (implying that light propagation really must be isotropic), observed time is still a valid phenomenological quantity. Language of appearance is very useful; we speak of sunrise and sunset (from Earth’s reference frame) when we know that it is actually the Earth that is rotating in the reference frame of the stars. (The Bible also uses such language.) The rest of this paper does not strictly require that observed time be an absolute (non-phenomenological) quantity. Those that hold rigidly to Einstein synchronization, may imagine that observed time is merely a useful phenomenological quantity—like the centrifugal or Coriolis forces (artificial forces introduced to make a rotating reference frame obey Newton’s laws).
The Biblical convention
Observed time requires less information than calculated time. Anyone can look at a clock when an astronomical event occurs and record the time. However, to obtain the calculated time, one must already know the observed time, as well as the distance to the object and the speed of light. The distance to an object is often unknown, or not known very accurately. This is why astronomers record events according to the observed time convention. Yet, astrophysical calculations are almost always done in calculated time. Each convention is useful for certain purposes. We now ask a critical question: Which definition of time does God use in Genesis 1:14-19 when He creates the stars? Are the stars created on the fourth day—observed time, or the fourth day—calculated time?
Observed time is always useful, but for calculated time to be meaningful we must know the distance to the object and the speed of light. Did the ancient Hebrews know the speed of light accurately? They probably did not. Did they know the distance to the stars? Again, they probably did not. In fact, only in modern times has calculated time become meaningful; we have only recently known the speed of light and the distance to the stars with any accuracy. So the question now takes on a different form: Would God have used a definition of time that would only become meaningful thousands of years later? If God’s definition of time on Day 4 of Genesis is calculated time, then it would have been useless for ages. It would have been incomprehensible to all humanity for thousands of years until technology had developed to the level where we could measure the speed of light and the distance to the stars.
To be clear, both calculated and observed time conventions are perfectly legitimate from a theoretical point of view. (In fact, there are an infinite number of valid synchrony conventions.) And calculated time is the preferred choice for many situations. However, of all possible synchrony conventions, only observed time does not require knowledge of the distance to the source of an observed astronomical event (such as a supernova). This makes it the perfect choice for communicating to cultures that do not know the distances to the stars.
Thus it seems logical that God’s definition of time would be observed time. This definition has always been meaningful and practical; it would have been understood by the ancient Hebrews, and is still meaningful today. God would want His words in Genesis to be understood by everyone throughout time. Moreover, if God had created the stars on Day 4 according to calculated time, Adam and Eve would have seen no stars in the night sky for over four years! The stars would appear to ‘blink on’ one at a time, year after year. Adam and Eve would have had the impression that God was still creating! This would be deceptive, so we conclude that God created the stars on Day 4—observed time.
We now understand that the Bible must record events according to the observed time definition. This means that the beginning of the universe on Day 1 happened instantaneously everywhere at God’s command, as measured from observed time. Further, it means that the stars were ‘really’ created on Day 4, and their light reached Earth instantly. This is exactly the impression we get from a straightforward reading of the text, and it seems quite consistent with the nature of God.
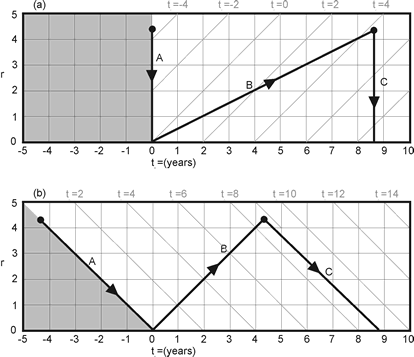
An alternative perspective
Since both calculated and observed time are consistent and meaningful measurements, it is always possible to convert from one to the other (Figure 2). We have seen that the Bible records events according to observed time; we will now convert these events into calculated time. This does not change what really happened, it just permits us another perspective. (The procedure is similar to converting cubits into feet in order get a feel for how big Noah’s Ark was in units we are comfortable with. Obviously, such a procedure would not actually change the size of the Ark.) If the reader is not convinced that observed time is as ‘real’ as calculated time, then he or she will consider this procedure a transformation from the apparent language of the Bible to a more physically objective reference frame.
Since the Bible indicates that the stars were visible on Day 4, we now compute the (calculated) time at which they were created. Alpha Centauri (a star 4.3 light years away) must have been created about 4.3 years ‘before the beginning’ (before Day 1) in order for its light to have reached Earth on Day 4 of the Creation Week. Likewise, a star 10 light years away must have been created about 10 years before Day 1. A star one billion light years away must have been created about one billion years ‘before the beginning’ and so on. So, we see that more distant stars were created earlier than nearby stars. The time of creation depends on the distance from Earth. So what appears to be simultaneous according to observed time, now appears to be spread out over a long period of time. Which view is the ‘correct’ picture? They both are—each according to the chosen convention of time measurement.
But how can a star be created before the beginning? We must remember that the Bible’s statement ‘In the beginning’ (Genesis 1:1) is a measure of time, and therefore must be the ‘beginning’ as measured according to observed time. So although the beginning of the universe occurs simultaneously everywhere on Day 1 according to observed time, the beginning of the universe (just as with the stars) occurs at different calculated times depending on the distance from Earth. Day 1 occurs much earlier for places in the universe that are more distant from Earth than nearby places.
So, we present the following picture of Creation as described in Genesis, but converted from observed time to calculated time—first, God creates the most distant sections of ‘space’. This occurs billions of years ago. About14 four days later, stars are created in those areas of space. As time passes, this creation process moves inward; space is created nearer to Earth, and stars are created four days later. About 4.3 years before Earth is created, ‘the beginning’ occurs for the space near Alpha Centauri. Four days later Alpha Centauri is created. Finally the Earth is created, but the starlight has not yet reached Earth; God provides a temporary light source. Four days later, God creates the Sun, the planets and the moon. At this point, (thanks to God’s innovative method of creation) all the light from all the stars reaches Earth at exactly the same time. This may seem an unusual method by which to create a universe, but then is there a ‘usual’ method by which universes are created? This method is compatible with the Word of God; and it is compatible with all astronomical observations of which I am aware. The God who created space and time should have no difficulty creating and placing the stars where and when He desires.
Now that we have converted to calculated time (and its consequent implication of ‘billions of years’), this view of the universe may sound a bit like an old-Earth Creation view or perhaps even similar to the big bang model. But the details are not similar at all, and astronomers who believe the big bang would not accept this view as being even remotely compatible with their ideas. Nor does this model promote the anti-Biblical idea of millions of years of death and bloodshed before Adam. The only similarity—this idea of ‘billions of years’—merely comes from the way in which we have chosen to define time, and does not reflect the duration of any actual process. The light from every star we see today should have been emitted when that star was about 6,000 years of age15 (regardless of which definition of time we use), and this is certainly not compatible with the big bang or any ‘old-Earth’ theory.
However, big bang theorists were not around when the universe was created.16 They might create stories about the past, but these speculations are beyond the scope of science. Only God was there at Creation, and He has given us some of the details of Creation in His Word. If we correctly understand His Word, and if our observations of the universe and subsequent calculations are correct, then the preceding model should be an accurate and truthful view of the creation of the universe.
Summary and conclusions
We have seen that the measurement of the time of an event is a subjective measure. We find that there are at least two useful conventions by which to measure time; calculated time and observed time. As measured by observed time, light travels instantaneously when moving toward an observer, but at different speeds in other directions. There does not appear to be any way to empirically test the unidirectional speed of light. Thus, observed time may very well be just as ‘true’ and fundamental as calculated time, though at the very least, it is a practical phenomenological measurement.
The Bible’s measurement of time must be observed time; calculated time has only become meaningful recently, but God would want His Word to be understood by everyone. As measured according to observed time, stars were created on Day 4—and their light reached Earth instantaneously—just as described in Genesis. The description of Creation as recorded in Genesis can be converted into calculated time if this is preferred. The claim that distant starlight disproves the Bible is a fallacy stemming from a mismatch of the definitions of time.
References
-
Humphreys, D.R., Starlight and Time: Solving the Puzzle of Distant Starlight in a Young Universe, Master Books, Green Forest, Arkansas, 1994.
-
Einstein, A., Relativity, The Special and General Theory, authorized translation by Robert W. Lawson, Crown Publishers, Inc., New York, 15th edition, 1959.
-
The speed of light for any given angle as measured in observed time is:
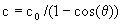
where c0 is the canonical speed of light (1,079 million km/hr) as measured in calculated time, and θ is the angle of the light relative to the observer.
-
Nissim-Sabat, C., A Gedanken experiment to measure the one-way velocity of light, British Journal of Philosophy of Science 35:62-64, 1984. (The claim is shown to be flawed in the following Ref. 5 and 6.)
-
Norton, J., The quest for the one-way velocity of light, British Journal of the Philosophy of Science 37:118-120, 1986.
-
Ohrstrom, P., Nissim-Sabat on the one-way velocity of light, British Journal of the Philosophy of Science 37:120-122, 1986.
-
The conversion between the calculated time (tc) and the observed time (to) of an event is: tc = to - r/c0 where r is the distance to the event and c0 is the (two-way time averaged) speed of light.
-
Anderson, R., Vetharaniam, I. and Stedman, G.E., Conventionality of synchronisation, gauge dependence and test theories of Relativity, Physics Reports 295:93-180, 1998.
-
Winnie, J., Special Relativity without one-way velocity assumptions: part I, Philosophy of Science 37:81-99, 1970.
-
Winnie, J., Special Relativity without one-way velocity assumptions: part II, Philosophy of Science 37:223-238, 1970.
-
Salmon, W.C., The philosophical significance of the one-way speed of light: Nous 11(3):253-292, Symposium on Space and Time, 1977.
-
Malament, D., Causal theories of time and the conventionality of simultaneity: Nous 11(3):293-300, Symposium on Space and Time, 1977.
-
Sarkar, S., and Stachel, J., Did Malament prove the non-conventionality of simultaneity in the Special Theory of Relativity? Philosophy of Science 66:208-220, 1999.
-
To avoid being overly technical, I have ignored the relativistic time-dilation due to the expansion of the universe. This effect is small for nearby galaxies, but becomes increasingly large for distant sections of space. The effect is not relevant to the fundamental concepts addressed in this paper.
-
The most distant stars would appear younger than 6,000 years due to relativistic time-dilation caused by the expansion of the universe.
-
Job 38:4.
Robert Newton is the pen name of a creationist astrophysicist currently undertaking research for a doctorate at an accredited university in the USA. He graduated summa cum laude, with a double major in physics and astronomy, and a minor in mathematics. He has also completed a M.S. in astrophysics. Robert is a member of the American Astronomical Society and Phi Beta Kappa.
Recommended Resources

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- Available Monday–Friday | 9 AM–5 PM ET
- © 2026 Answers in Genesis

