The Analemma and Flat Earth

If you have looked at an old globe, you may have noticed a figure-eight shape somewhere in an empty part of the Pacific Ocean where there are no large islands (See Figure 1). This figure-eight shape is called an analemma. I don’t know why globe makers used to put analemmas on their globes, or why they stopped including analemmas on globes by the 1960s. Perhaps they put the analemmas there to take up otherwise empty space, and maybe they eventually took them out because few people knew what the analemma is or what to do with it. When in grade school 60 years ago, I noticed the analemmas on globes, though I didn’t know what they were called. My classmates and I noticed that dates were marked on it, and we figured out that it showed at what latitude the sun was directly overhead at local noon as a function of date, but we couldn’t figure out the figure-eight shape. A decade later, I found out not only the name of the analemma but also what it is. Before I get to that, let me explain why I am discussing the analemma.

Flat-Earthers and the Analemma

Flat-earthers often bring up the analemma, usually accompanied by the claim that the analemma cannot exist if the earth is spherical and makes sense only on a flat earth. Here is one example of this claim. Few flat-earthers know what the analemma is. Some flat-earthers seem to think that the analemma is a spiraling motion that the sun makes in the sky. I can understand why some people might get that impression—the analemma now is often photographic rather than graphical, such as the one in figure 2. This was the first photographic analemma, published on pages 536–537 of the June 1979 issue of Sky and Telescope magazine. This was back in the days of film, long before digital cameras were available. I created Figure 2 by photographing with my digital camera those two pages of my copy of the magazine.

This historical 1979 photograph was captured on a single piece of film exposed on 45 dates throughout the year. The camera remained firmly mounted the entire time. This was the second attempt. Figure 3 shows another photograph from the next page of the same issue of Sky and Telescope, showing that on the first attempt, the camera was mounted too low, thus cutting off the top of the analemma. Therefore, it took two years to complete this project. With digital cameras so readily available (and I suspect in some cases altering digital images, such as with Photoshop), these sorts of photographs have become much more common. Unfortunately, these photographs have led people astray. For instance, if one looks up the definition of the analemma now, it is often defined in terms of how such photographs are produced. The analemma was known and plotted (often on globes) long before 1979, when the first photographic analemma was made, so these modern definitions miss the point. The French astronomer Jean-Paul Grandjean de Fouchy introduced the analemma in 1740, formalizing its modern usage, long before photography existed. In fact, the concept of the analemma even dates back to ancient Greek astronomy, such as during the time of Ptolemy (second century AD).

What Is the Analemma?

The analemma is a plot of the relation between the sun’s declination and the equation of time. What do these terms mean? Astronomers use declination and right ascension to locate celestial objects in the sky. These two coordinates are similar to latitude and longitude on the earth. There are celestial poles in the sky, as well as a celestial equator, from which declination is measured. The ecliptic is the plane of the earth’s orbit around the sun. The ecliptic is inclined 23.4 degrees to the celestial equator. If you recognize the 23.4-degree angle to be the earth’s tilt, it is no accident. Because of the earth’s axial tilt, the ecliptic must be inclined 23.4 degrees to the celestial equator. The celestial equator is the plane of the earth’s equator projected onto the sky. As the ecliptic is the earth’s orbital plane, the celestial equator is the earth’s rotation plane. Astronomers call the 23.4-degree angle between the ecliptic and the celestial equator the obliquity of the ecliptic. As the earth orbits the sun throughout the year, the sun appears to move west to east along the ecliptic, taking one year to complete one circuit. Consequently, the sun’s declination changes, ranging from -23.4 degrees to +23.4 degrees. Figure 4 shows the declination of the sun as a function of date. Notice that the sun’s declination is zero degrees on the equinoxes and has a maximum 23.4-degree magnitude on the solstices. At any given date, the sun’s declination corresponds to the latitude where the sun appears directly overhead at local noon, as my classmates and I figured out in grade school. (This latitude shifts between the Tropic of Cancer [+23.4 deg] in June and the Tropic of Capricorn [-23.4 deg] in December.)

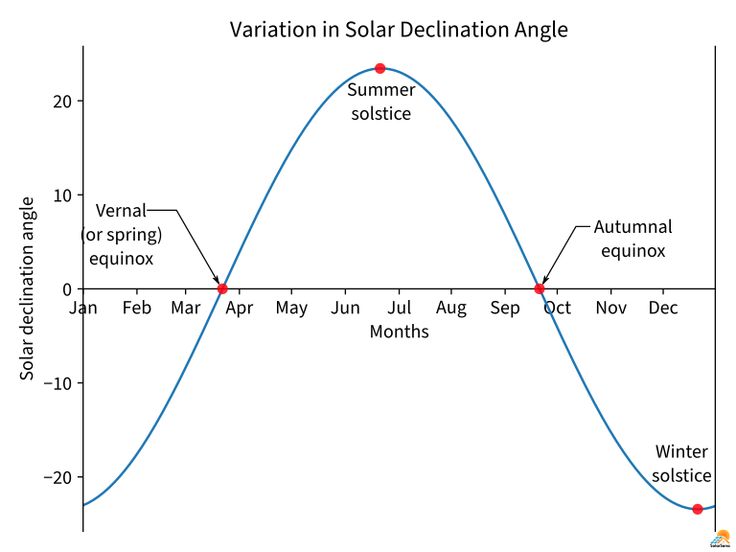
The analemma is a plot of the relation between the sun’s declination and the equation of time.

So far, so good. This explains the vertical part of the analemma, but what about the horizontal part that gives the analemma its figure-eight shape? We tend to mistakenly think that the sun keeps perfect time, but it doesn’t. Local noon is defined as when the sun is as high in the sky as it can get. As the sun appears to move east to west across the sky each day (due to earth’s rotation, not because the sun itself is moving), the sun first gets higher in the sky until noon. But after noon, the sun gets progressively lower in the sky. On average, it takes 24 hours for the sun to go from one noon to the next, but the time from one noon to the next noon usually is a little longer than 24 hours or a little less than 24 hours. Simply put, the actual length of the solar day varies slightly throughout the year. Why is this?

As the sun appears to move east to west parallel to the celestial equator each day, the sun also appears to move the opposite direction, west to east, along the ecliptic, albeit at a much slower rate. Over the course of a year (365.25 days), the stars appear to spin 366.25 times, so the speed of the sun as it moves west to east along the ecliptic is 1/366.25 the daily east-to-west motion of the sun parallel to the celestial equator. Assume for the time being that the sun’s slow apparent motion along the ecliptic is uniform (in reality, it’s not uniform because earth’s orbit is an ellipse). The daily motion of the sun is parallel to the celestial equator, so time is reckoned by the sun’s movement with respect to the celestial equator. Near the solstices, the sun’s annual motion along the ecliptic is parallel to the celestial equator. But near the equinoxes, the sun’s annual motion along the ecliptic is tilted 23.4 degrees to the celestial equator. See Figure 5. The solid horizontal arrow at the top represents the west-to-east motion of the sun along the ecliptic at the solstices, and the diagonal solid arrow represents the west-to-east motion of the sun along the ecliptic at the equinoxes. The two arrows are the same length. However, notice that the projection of the sun’s motion onto the horizontal celestial equator on one of the equinoxes (the dashed arrow) is foreshortened as compared to the sun’s motion when at one of the solstices. The result is that near the equinoxes, from one noon to the next noon will be slightly less than 24 hours. On the other hand, near the solstices the length of time from one noon to the next will be slightly greater than 24 hours. These differences from 24 hours will last for many weeks, and the difference in time each day will accumulate. While the average length of time from one noon to the next is exactly equal to 24 hours, daily the sun will run fast for a while and then run slow for a while. The accumulated error can amount to nearly 16 minutes.

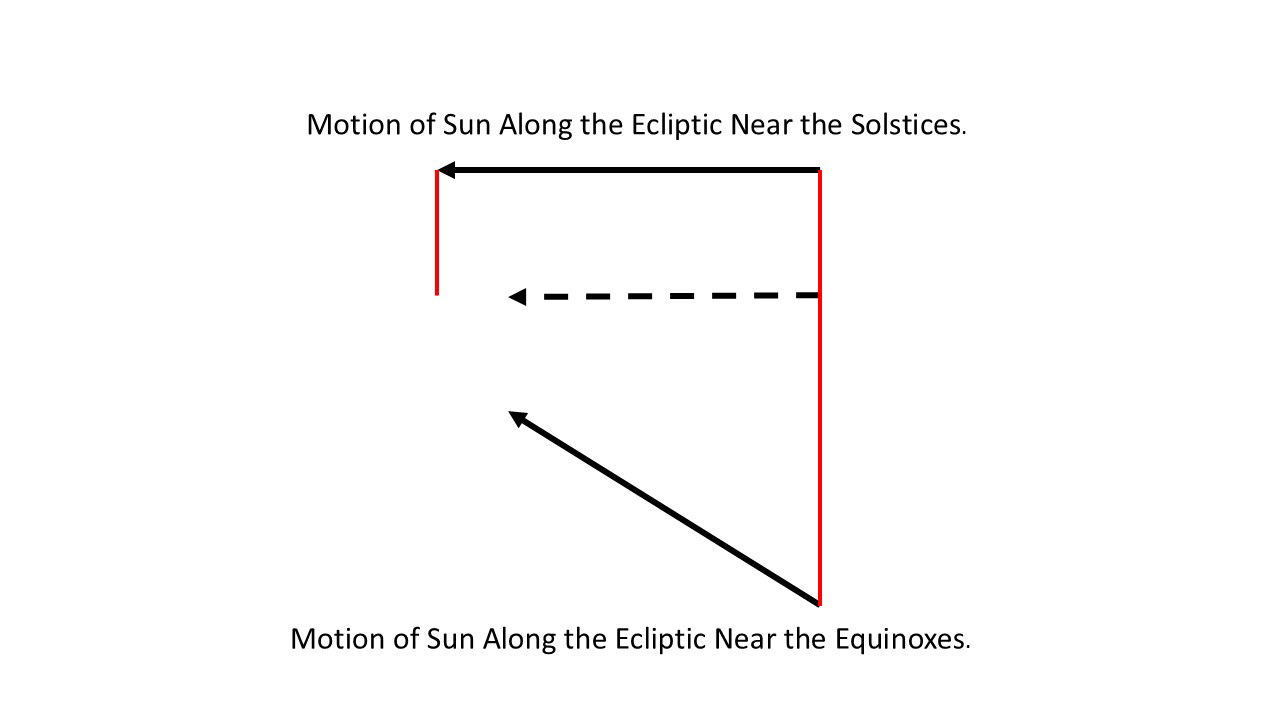
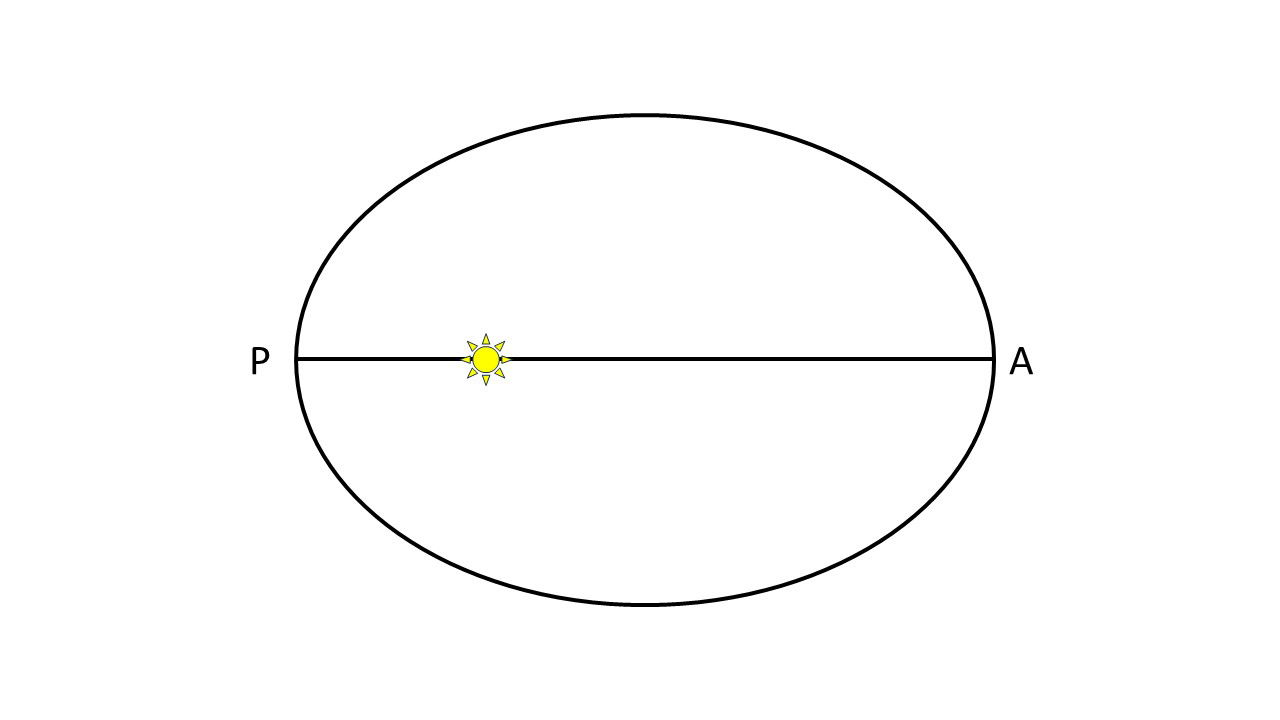
We assumed that the sun appears to move along the ecliptic at a uniform rate, but this is not true. Why not? The earth’s orbit around the sun is an ellipse (an oval shape with two focal points, with the sun located at one of the points), with earth being closest to the sun at a point we call perihelion and the earth being farthest from the sun at a point we call aphelion. Figure 6 illustrates these concepts. For clarity, the elliptical nature of the earth’s orbit has been exaggerated in the figure—in reality, the earth’s orbit is nearly circular. Perihelion is indicated by a letter P, and aphelion is indicated by a letter A. The earth moves most quickly near perihelion (in early January) and most slowly at aphelion (in early July ). Therefore, in early January, the sun appears to move most quickly along the ecliptic and move most slowly in early July. However, this effect is less significant than the obliquity of the ecliptic.

Until the invention of very accurate chronometers (instruments for measuring time), such as the pendulum clock in the seventeenth century, there was little to no consequence of the sun running a bit slow or fast throughout the year. But once accurate timepieces were available, the sun’s variable time keeping became obvious. Most people assume that sundials keep good time, but they run fast and slow as the sun runs fast and slow. We define apparent solar time with respect to the position of the apparent, or real, sun, and so a sundial reads apparent solar time. Mean solar time is defined in terms of a mean, or average, sun with the irregularities just discussed smoothed out. Therefore, with mean local time, each noon is followed by another noon exactly 24 hours later. The equation of time is the difference between mean and apparent solar time. Figure 7 is a plot of the equation of time as a function of date (notice that it crosses zero four times per year, which happens around mid-April, mid-June, early September, and late December).

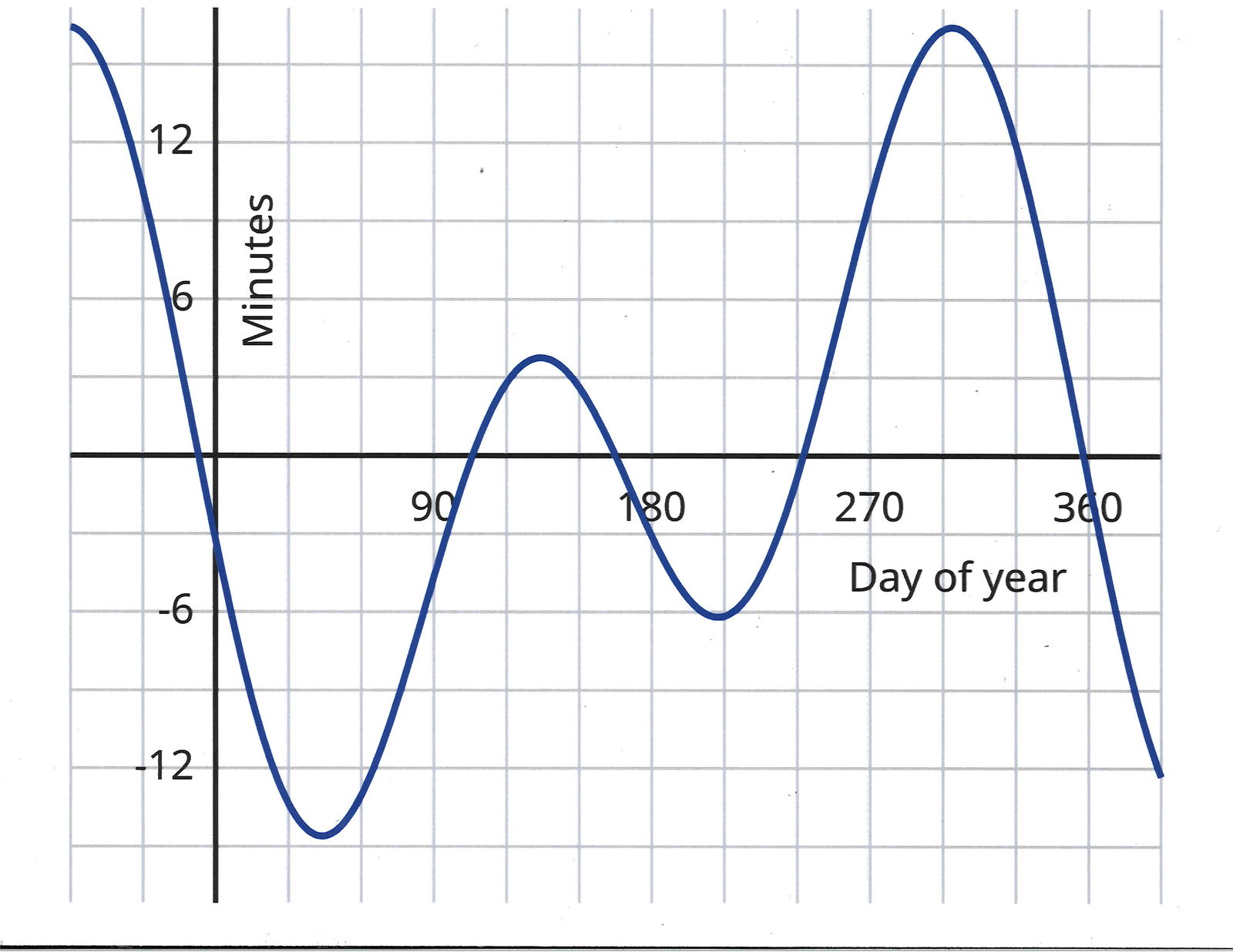
Mean solar time is the basis of time reckoning that we use. Mean solar time is sometimes called local time. However, the time that we keep is standard time, which is synchronized across time zones rather than tied to local solar noon, based upon a standard meridian of longitude. For instance, Eastern Standard Time (EST) in the United States is the local time on the 75th meridian west longitude. Converting the apparent solar time read on a sundial to standard time is a two-step process. First, one must add the equation of time to convert from apparent solar time to mean solar time. Second, one must correct for how much one’s longitude is from the standard meridian. This correction amounts to four minutes of time for each degree of longitude.

Keep in mind that the apparent sun is the real sun, but the mean sun is a fictitious sun (i.e., a mathematical construct used for timekeeping), with the irregularities of the real sun averaged out. Recently, I have noticed some flat-earthers have begun talking about the apparent sun. From the context of their conversation, these flat-earthers seem to think that the apparent sun is where the sun appears to be in the sky, implying that the real sun is somewhere else in the sky. This has it backward—the apparent sun is where the real sun is, not some sort of illusion or projection. It is not to be confused with the mean, fictitious sun that moves at a constant rate with respect to the celestial equator. Flat-earthers seem to misunderstand the term “apparent” sun, thinking that it’s a difference between where the sun appears and its actual location, and thus generally misunderstand the analemma.

Both the equation of time and the sun’s declination are functions of date, having a period of one year, and thus vary over the year. Removing the parameter of date, the relation of the equation of time to declination can be tabulated, or it can be expressed graphically. The analemma is a parametric plot of this relation, with the declination on the vertical axis (this tells us the sun’s position north or south of the celestial equator) and the equation of time on the horizontal axis (this tells us how much the apparent solar time differs from mean solar time on a given day). Since the apparent (real) sun runs fast part of the year and slow part of the year, the analemma has a figure-eight shape. The analemma often is calibrated with date along its figure-eight shape. That is how my classmates and I were able to figure out at least part of the analemma 60 years ago.

How the First Photographic Analemma Was Made

How was the photograph shown in Figure 2 made? The camera faced to the southeast and captured the sun’s image at the same standard time on each of the 45 days throughout the year. Obviously, a solar filter was used for these images, and a single unfiltered image without the sun in the view provided lighting for the landscape in the photograph. In this particular case, the three long streaks resulted from long exposures showing the sun rising, taken on three days, one near the June solstice, one near the December solstice, and one in between when the equation of time was zero. If there were no equation of time, then the sun’s image would have been a line of solar images spaced out along the longer axis of the analemma (declination variation only). Alternately, if the images were taken at the same apparent solar time (as read on an accurate sundial), then the effect would have been the same. The angle that the long axis makes with the horizontal is dependent on the latitude and the time of day the images were taken.

Conclusion

The analemma is evidence that the conventional (real-world) cosmology is true.

I chose my words very carefully so that the analemma is observationally defined, without definitions demanded by either a spherical or flat earth (though I did give the conventional explanation as well). Hence, flat-earthers and globe-earthers ought to agree on what the analemma is without resorting to claims that it works only on one model of the earth or the other. Flat-earthers don’t seem to understand this. I conclude that is because flat-earthers generally don’t know what the analemma is. The best I can figure is that many flat-earthers think that the sun actually spirals around in this shape in the sky—an imaginary scenario. In the real world, it doesn’t. As for an explanation for why the analemma exists, flat-earthers have no coherent explanation, other than the fact that it just does (an appeal to ignorance fallacy). On the other hand, sprinkled throughout my discussion, I have included the conventional explanation for the analemma—it is a combination of the obliquity of the ecliptic and the earth’s elliptical orbit. This explanation is straightforward with no special pleading. Therefore, the analemma is evidence that the conventional (real-world) cosmology is true. No alternative model—including the flat-earth “cosmology”—provides a real explanation for the analemma.