Second Flat Earth International Conference

Last year I attended the first Flat Earth International Conference near Raleigh, North Carolina. On November 15–16, 2018, I attended the Second Flat Earth International Conference in Denver. I blogged about last year’s meeting, so here I take the opportunity to blog about this year’s meeting.

There were presentations all day on both days of the conference. Unlike last year, this year there were some parallel sessions that required attendees to choose which of two sessions that they wanted to attend. This was good, for not only did it allow for more presentations, but it gave attendees another option if one presentation did not suit their fancy.

I approached the first meeting with apprehension, not knowing what to expect. I went to that meeting with the intent to fly under the radar, hoping that not too many people would take notice of me. That proved difficult, as many attendees were friendly and struck up conversations with fellow attendees, with among the first questions asked being how long others had believed the earth was flat. It’s difficult to answer that question without letting people know right up front that I didn’t believe that the earth is flat. Plus, a couple of people recognized me, and word of my presence soon spread. As it turns out, my fears were unfounded, because the people I talked to last year were kind and glad that I was there.

Therefore, I approached this meeting with a very different attitude: I wanted to engage people from the very beginning. I wanted to find out “what made flat-earthers tick,” so I talked to many people, asking such questions as how long they had been into flat earth, what had convinced them that the earth was flat, and some specifics about which particular flat-earth model they believed. Many of the people I informally interviewed in this way didn’t know at first that I wasn’t a flat-earther. I wanted it that way, because I feared that if they knew that I wasn’t a flat-earther, it might alter their answers. Of course, when asked, I told them that I didn’t believe that the earth is flat. Most conversations didn’t end before that was revealed. I am pleased to report that all the people that I talked to were very pleasant, and so I enjoyed the meeting very much. I feel that I made some friends at this meeting. I wasn’t at the meeting to debate, argue, or convince anyone. This is difficult for me to do, but I think that I managed it well. And I did a lot of listening, something that I’m also not too good at. At least that’s what my wife says. She’s probably right.

This meeting was different from last year’s meeting.

This meeting was different from last year’s meeting. Last year, many of the speakers and conference attendees emphasized acceptance, the good feeling to be among people who believed the same thing that they did. That wasn’t so obvious this year. One complaint that I had with last year’s meeting was that I didn’t see or hear too much new. Nearly all that was presented I had seen on the internet and other places already. However, many of the presentations this year went into greater detail. The theme of this year’s conference was “Taking it to the Next Level.” I guess in this sense the conference delivered on that.

The Debate

The highlight of the conference for many people was the Thursday evening debate between Rob Skiba and Robert Sungenis over whether the Bible teaches that the earth is flat. Sungenis is best-known for his documentary The Principle, in which he argued for geocentrism. Many flat-earthers conflate geocentrism and flat earth. Since both participants in the debate believe in geocentrism, that part of the argument was removed from discussion. Either participant gave a 30-minute opening statement, followed by a 15-minute rebuttal and a 15-minute closing statement. The styles of the two men were very different. Skiba had prepared PowerPoint presentations for his opening statement, rebuttal, and summation, while Sungenis didn’t use any visual aids.

By the toss of a coin, Skiba went first. He began by quoting Sungenis that the raqia, translated “firmament” in the King James Version of the Bible is a hard dome over the earth. My immediate reaction was that if this were true, then perhaps the debate was over before it began. However, in his opening statement, Sungenis stated that he believes, as his Roman Catholic Church teaches, that the Bible ought to be interpreted literally, except when that doesn’t work. Sungenis then proceeded to show how the raqia could not be a solid dome. For instance, if the raqia were a solid dome, then the placement of the sun and moon in the solid dome on Day Four would inhibit the sun and moon from moving, which, in anyone’s model, they must move. I thought that that was a very effective counter to what had appeared to be a devastating blow in Skiba’s initial presentation. And this is the way that the debate went: Skiba was aggressive when on the offensive, while Sungenis was masterful at rebuttal. In their rebuttals and conclusions, there was much discussion over a preposition in a few biblical passages and how it is to be understood properly. I’m sure that many people in the audience thought that this was whacking in the weeds.

Things got a little weird in Skiba’s rebuttal. He had a slide that included a photograph of me, along with a quote from my 2004 book, Universe by Design, where I criticized the way that the Septuagint and Vulgate translated raqia, and consequently how the King James translated raqia as “firmament.” Skiba said that this was eisegesis. He also called Answers in Genesis “Answers not in Genesis.” I was a bit amused by this, because Skiba was rebutting me, when I wasn’t involved in the debate. Skiba returned to this slide again in his concluding remarks.

Who won the debate? Overall, I thought both men did a good job of representing their positions. This wasn’t a formal debate, and their styles were so different, it made it difficult to determine who, if either, won. Part of the problem with debates is that most observers end up thinking that the debater that they agree with won. And several attendees later expressed their opinion that Skiba won hands down. But that is to be expected, seeing that Sungenis was in a largely hostile audience.

Meeting the Speakers

I made it a point not only to talk to many attendees, but also to introduce myself to most of the speakers and leaders in the flat-earth movement. I previously had met Rob Skiba and Robbie Davidson, though I spoke with both again this year. I met Mark Sargent, Jeran Campanella, Darryle Marble, Nathan Roberts, Bob Knodel, Zen Garcia, and Rick Hummer. Hummer and I hit it off well – we have similar senses of humor, and we share at least a couple of other things in common: roots from eastern Kentucky and time spent in South Carolina. I even shared a few hillbilly jokes with him. People who know me well know that I love hillbilly jokes. I also briefly spoke to Robert Sungenis. Though we knew of one another, we had never met.

Bob Knodel, Again

My discussion with Bob Knodel was interesting. He obviously had read my blog about last year’s meeting, for almost immediately he brought up my critique of some of his comments in his “Globe Busters” presentation last year. He said that I was wrong, and he intended to do a rebuttal. I insisted that what I had said was correct, but he strongly disagreed. A bit later, during his “Globe Busters” presentation for this year, Knodel referred to me, though not by name. He then proceeded to double down from last year. He insisted that if one applies to stars the inverse square law and decreasing angular size with increasing distance, we ought not to see the stars if the stars are as far away as astronomers think (it was Knodel’s comments along this line that I critiqued from last year). To illustrate the point, Knodel further asserted that if the sun were moved to just one light day away, it wouldn’t be visible. He emphasized that this would place the sun at the outer edge of the solar system, so this proved that stars, if they are as far away as astronomers believe, would be invisible. My complaint with Knodel last year was that he obviously didn’t bother running the numbers for his claims, which is strange for an engineer. But once again this year, Knodel failed to run the numbers on this claim. I will run the numbers for him.

The sun is 8.3 light minutes away. Therefore, if the sun were one light day, then it would be (60/8.3) x 24 = 173.5 times farther away than it is now. Following the inverse square law, if the sun were moved this far away, it would appear 1/(173.5)² = 1/30,100 times as bright as it appears now. The sun is about 400,000 times brighter than the full moon. Therefore, if the sun were one light day away from us, it would appear 400,000/30,100 = 13.3 times brighter than the full moon. Since the full moon is a relatively bright object, the sun still would be quite bright in the sky if it were a light day away. Therefore, Knodel clearly is wrong about this.

Knodel expressed concern about the angular size of the sun if it were this far away. The sun currently is about ½ degree across. Angular diameter is inversely proportional to the distance, so if the sun were moved to one light day away, it would subtend an angle of (1/2)/173.5 degrees = 0.0028 degrees = 0.18 arcminutes. The naked eye can see an angle of about one arcminute, so if the sun were this far away, we could not make out its apparent disk without optical aid, i.e., the sun would be a tiny point, like other stars. Expressed another way, all the light of more than 13 full moons would be crammed into a tiny dot that the eye could not resolve. This would render the sun so dazzlingly bright, you could not look directly at it. So much for Knodel’s claim on this. The only thing that I can figure is that Knodel must think that the inverse square law and the decreasing angular size with increasing distance somehow combine to make the sun too faint to be seen. But that isn’t how it works.

However, there is another possibility of what Knodel meant. At the meeting, I took the opportunity to purchase from vendors reprints of several books about flat earth, mostly from more than a century ago. I wasn’t aware that some of these books were available again. One book that I purchased was the second half of Alexander Gleason’s 1893 book, Is the Bible from Heaven? Or Is the Earth a Globe? In this book, Gleason discussed the decreasing angular size of objects with greater distance as an argument for why we supposedly can’t see astronomical bodies, if they are as far away as astronomers think. Gleason mentioned that round objects viewed from a distance 3,000 times greater than their diameters or more cannot be seen. At this distance, a round object will appear about one arcminute across, rendering its angular extent indistinguishable to the naked eye. Gleason misunderstood this to mean that a luminous object would be invisible from this distance. Perhaps this is what Knodel was thinking of. But this is incorrect, because even though the naked eye couldn’t make out the angular diameter of such an object, if the object were bright enough, its light still would be visible. Consider the high intensity flash lights that are so popular today. Many of those flashlights have lights that are only an inch in diameter. Three thousand inches is only 250 feet. But the beams of such flashlights don’t magically disappear at distances greater than 250 feet. Rather, at night the beams of these flashlights can be seen at much greater distance than 250 feet, though the naked eye can’t make out the angular size of the light. The angular diameters of stars are very small. For instance, the bright star Betelgeuse has a measured angular diameter of 0.050 arcseconds. That is 1/1,200 of an arcminute, the smallest angle that the unaided eye can make out. Therefore, Knodel’s conclusion about this is completely wrong.

In their presentation, the Globe Busters (Bob Knodel, Jeran Campanella, and Iru Landucci) also said that the inverse square law proves that we didn’t send astronauts to the moon. They reasoned that as one gets closer to the moon, the moon must appear much brighter, which is true. For instance, following the inverse square law, at half the distance to the moon, the moon would appear about four times brighter. At one-tenth the distance to the moon, the moon would appear 100 times brighter. When the astronauts were 1/100 the distance to the moon, the moon would appear 10,000 times brighter. They asked how much brighter the moon would be when astronauts arrived at the moon. This simple analysis would suggest that the moon would be blindingly bright. So why didn’t the moon look that bright in the photos taken from the lunar surface?

To many people, this sounds very reasonable, and hence this seems a devastating argument against the idea that Apollo astronauts went to the moon. However, this analysis leaves some very important things out. One thing left out is that the inverse square law assumes a point light source. The moon is an extended light source, not a point light source. When viewed from great distance, the moon can be treated as a point source as an approximation, but keep in mind that this is an approximation. As the distance to the moon decreases, this approximation breaks down. This brings up a related issue: with changing distance, we see varying amounts of the lunar surface. Being 240,000 miles from the moon, we see nearly ½ of the moon’s total surface area. However, as one approaches the moon, one sees progressively less and less of the moon’s total surface. From the lunar surface, only a very tiny portion of the moon’s surface would be visible. Yet, the analysis that the Globe Busters did was based upon the entire (nearly) half of the moon’s surface that from earth would be visible all the way to the moon and even on the lunar surface. Fortunately, it is relatively straightforward to compute how much of the lunar surface is visible as a function of distance from the moon and hence correct for this effect.

Figure 1 illustrates the situation. The circle with center C and radius R represents the moon. The observer is at point P at distance PC = r from the moon’s center. The observer can see to point A on one side of the moon and to point B on the other side. The triangles PAC and PBC are congruent. This is a two-dimensional representation – the three-dimensional representation is obtained by spinning these two triangles around the line PC. This transforms the two triangles into a cone having its apex at P and its base being the circle passing through points A and B and having its center along the line PC. The base of this cone inscribes a cap on the spherical moon that is visible to the observer at point P, as shown in Figure 2. Notice that less than half of the surface of the sphere is visible to the observer at point P. As is shown in Figure 3, the distance to the moon decreases, the size of the visible cap diminishes. As the distance to the moon increases, the area of the cap visible approaches one half the entire lunar surface. Let the angle of either triangle at point P be θ. Then,

θ=sin^-1⁡(R/r)

The area of a cap is given by

A=2πR²(1–cosθ΄),

Where θ΄ is the angle at point A or point B. Since triangles PAC and ABC are right triangles, θ΄ is the complement of θ. Since for complementary angles cosine (θ΄) = sine (θ), we can rewrite the above equation as

A=2πR²(1-sin⁡θ).

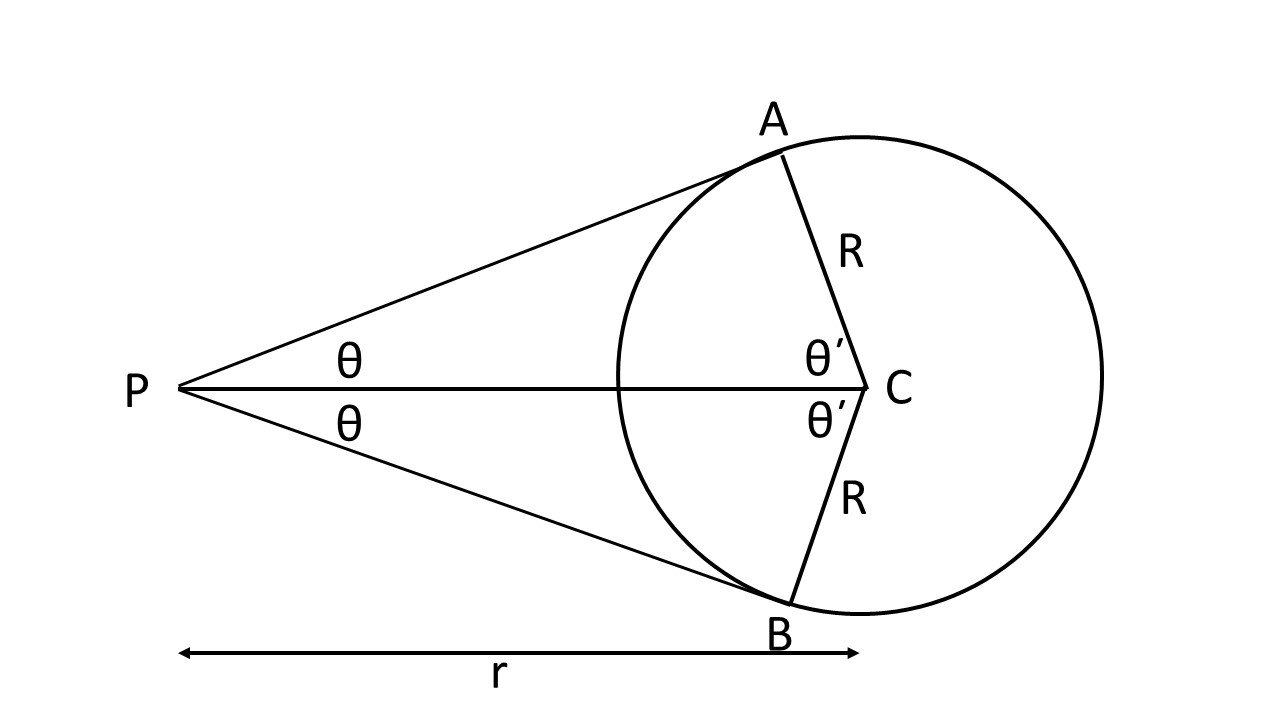
Fig. 1. At point P at a distance r from a sphere having radius R, an observer sees only the cap of a sphere of inscribed by points A and B.

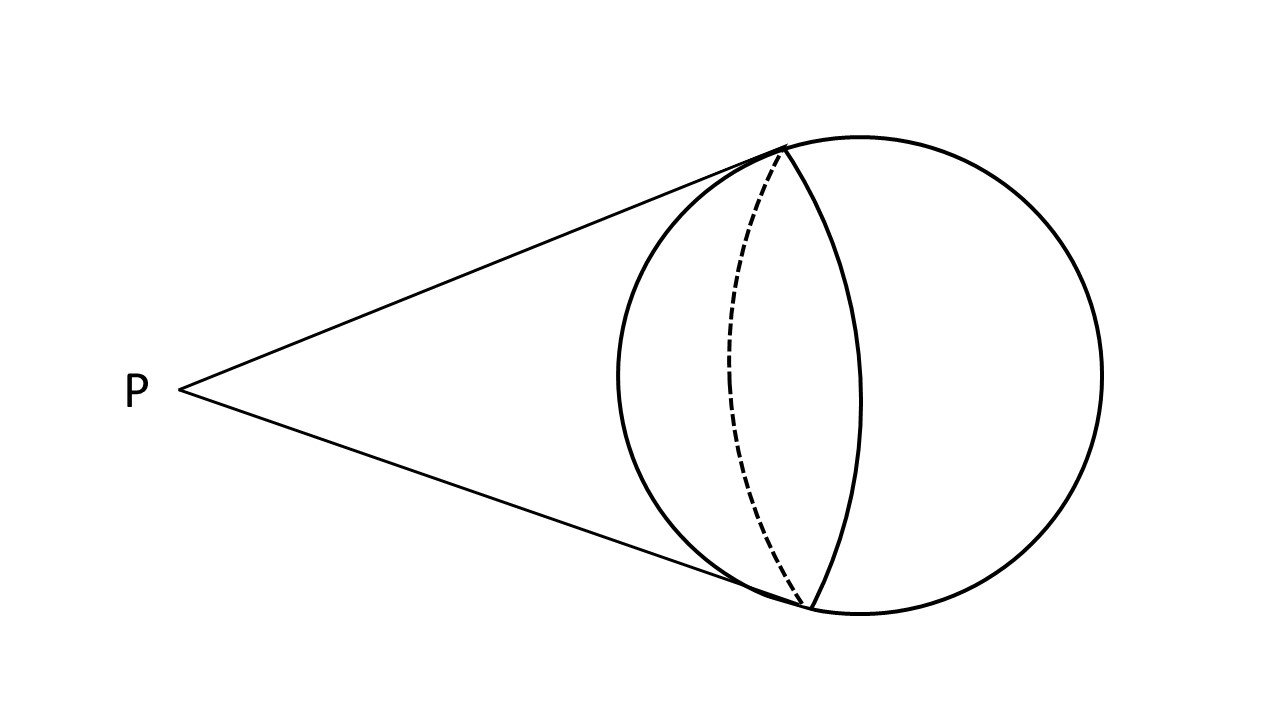
Fig. 2. The cap on the sphere visible from point P.

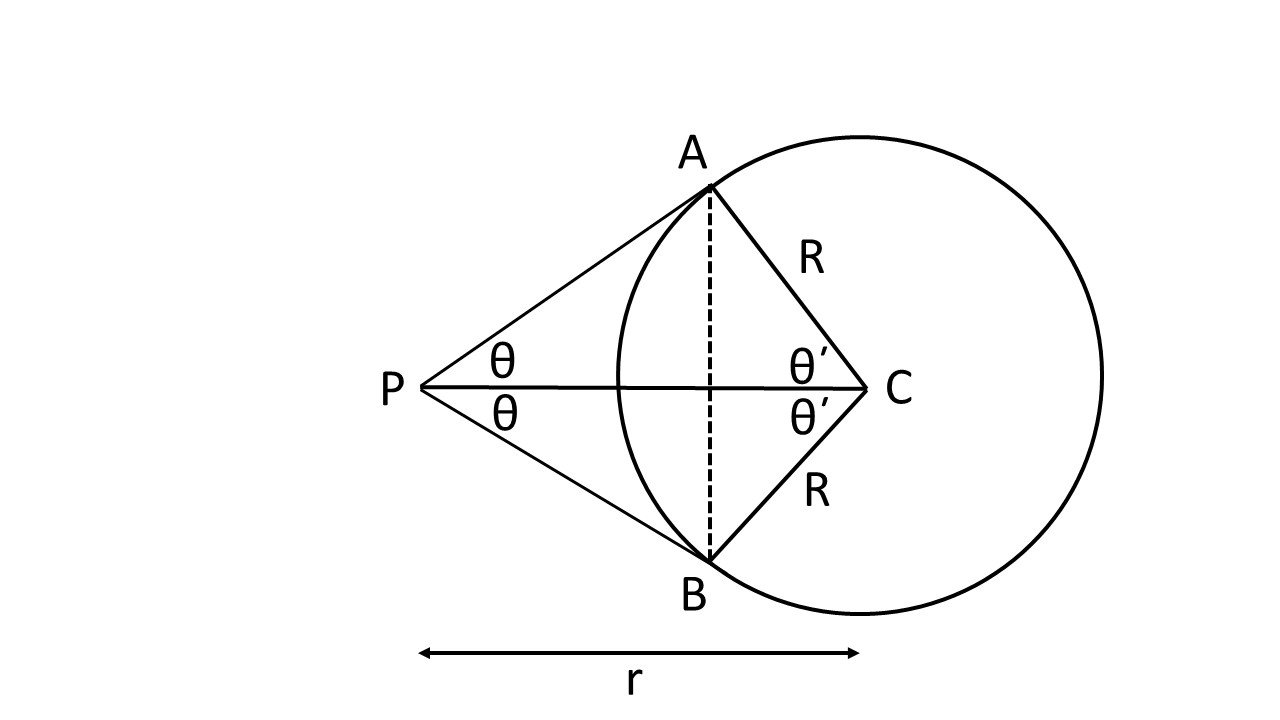
Fig. 3. Figure 1 but showing a smaller distance r. Notice that now the distance between points A and B is smaller, resulting in a smaller visible cap than before.

Let I₀ be the intensity of the moon at the moon’s distance from the earth, D, approximately 240,000 miles. Then according to the inverse square law, the moon’s intensity, I, at a distance d will be

I=I₀/(d/D)²

Figure 4 shows this simple inverse square calculation of the moon’s brightness in terms of I₀ as a function of relative distance that the Globe Busters discussed. The distance between the earth and moon is along the horizontal axis, expressed as a fraction of the 240,000 miles separation of the earth and moon. Essentially, the moon is on the left, and the earth is on the right on this plot.

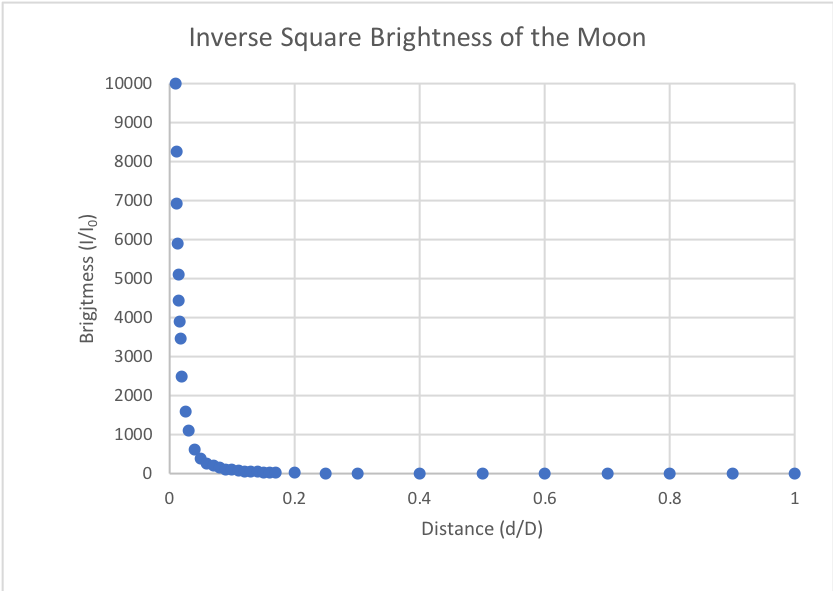
Fig. 4. The inverse square relationship of brightness, expressed in terms of the intensity of the moon, I₀, at 240,000 miles. The distance is expressed as a fraction of the 240,000 distance to the moon, D.

The moon’s brightness on the vertical axis is expressed in terms of the moon’s brightness as seen from earth. Therefore, on the far right, where the relative distance to the moon is equal to one, the moon’s brightness is defined as one. Notice that at distance equal to 0.01 (2,400 miles from the moon’s center), the brightness is 10,000. As the separation goes to zero, the intensity increases without bound.

However, as discussed above, this overestimates the moon’s apparent brightness, because it assumes that the entire portion of the spherical moon visible from earth would be visible all the way to the moon. To account for a diminishing amount of the moon being visible as one approaches the moon, one must correct the above equation by dividing by the portion of the moon visible from the earth and multiplying by how much of the lunar surface is visible at any given distance. These two factors are computed using the first equation above to find the angle θ at any distance r, and then computing the area visible using either the second or third equation.

Figure 5 shows this correct analysis on the same scale as the first plot. Notice that from the earth down to 10% of the distance to the moon, the two plots agree very well. However, note that in the last 10% of the distance, the two curves begin to diverge. Instead of increasing without bound as the distance from the moon goes to zero as the first plot does, the second plot reaches a peak before dropping back down. To see the behavior of this function better, Figure 6 shows the last 10% of the second plot on a different scale. The brightness peaks at a little more than 2,140 times the brightness of the moon as seen from earth. This peak occurs around 1.25% the total distance from the moon. This is 3,000 miles from the moon’s center, or about 2,000 miles from the lunar surface. At this distance, the moon would subtend an angle of about 40 degrees. That is, while the peak brightness is more than 2,000 times brighter than how bright the moon appears from earth, this light is spread over 6400 times the angular area, rendering the surface brightness of the moon from this distance less than when viewing the moon on earth. As one gets close to the moon beyond this point, the total lunar brightness diminishes, largely because the amount of the lunar surface visible rapidly declines as one nears the moon. Therefore, the Globe Busters’ analysis is flawed, and this is no problem for the fact that Apollo astronauts did go to the moon.

Fig. 5. The inverse square relationship corrected for diminishing amount of lunar surface visible as one gets closer to the moon.

---

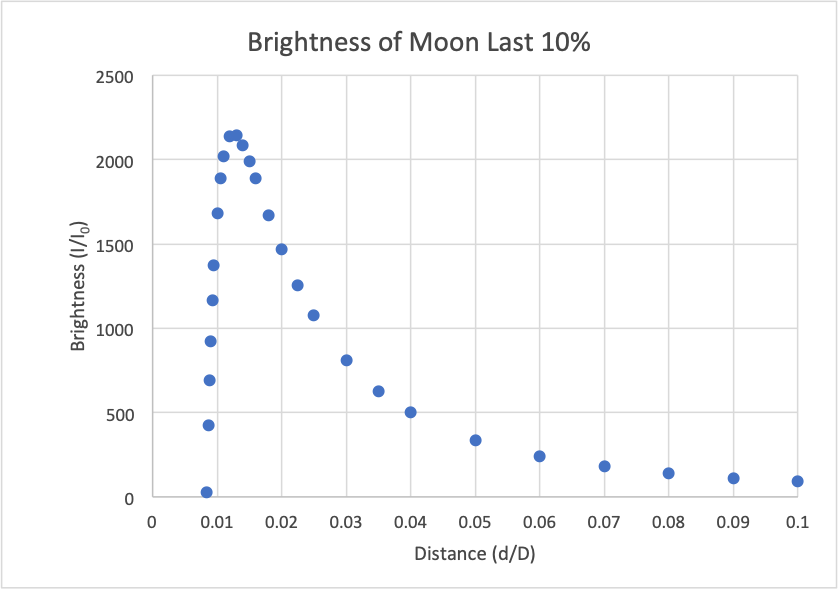
Fig. 6. The final 10% of Figure 5 replotted on a different scale.

Zen Garcia

Zen Garcia gave a presentation entitled “Biblical Cosmology.” Since I’m mostly interested in the Christian variety of the flat-earth movement, I was very interested in hearing this talk. However, I was disappointed by the content. The only biblical text that Garcia mentioned was Joshua 10:13, and then only briefly. He also made mention of a short passage from Ecclesiastes, but then only from the Targum, ancient expositions about what the Hebrew Scriptures say, but not explicitly from Ecclesiastes. If Garcia didn’t use the Bible, then what did he talk about? Garcia made many references to the Book of Enoch, as well as a few other non-biblical texts. The pseudepigraphal Book of Enoch teaches that the earth is flat, so it is a favorite of flat-earthers, some going as far to claim that it ought to be part of the Canon. I’ve previously critiqued the Book of Enoch in the context of flat earth. To make matters worse, Garcia ended his presentation with reference to sacred texts of India. What this has to do with biblical cosmology is a mystery to me. Garcia failed to deliver on the promise of the title of his talk. It should have been entitled “The Cosmology of the Book of Enoch and other Ancient texts”

Some flat-earthers seem to make belief in flat-earth as an essential doctrine of Christianity.

Two other things that Garcia said concerned me. He was on a panel that took questions from the audience on “Flat Earth and The Bible.” In his opening statement, Garcia said that flat earth had everything to do with salvation. I don’t know what he meant by that. Some flat-earthers seem to make belief in flat-earth as an essential doctrine of Christianity. Is that what he meant? In response to a question posed to the panel, Garcia said that the sun, moon, and other zodiacal bodies (the planets) have an effect upon people. That sounds like astrology.

Oh, Gravity

Paul on the Plane and Knoxy gave a presentation entitled “Oh, Gravity.” Of the talks that I attended, this had to be the most unintelligible. Flat-earthers dispute whether gravity exists. They claim that it’s just a theory and has never been proven. Then what causes most things to fall downward? Flat-earth opinions vary on that question. One idea is that what we perceive as gravity is an effect of magnetism. Maybe electricity and magnetism. You see, it isn’t very clear. But the majority opinion among flat-earthers appears to be that what we perceive as gravity merely is an effect of buoyancy. Paul on the Plane and Knoxy attempted to flesh out that idea. Everyone seems to agree that objects denser than air tend to fall, while objects less dense than air tend to rise. But what causes that? Flat-earthers must think that this is just the way the world works. The conventional understanding is that objects in a fluid (such as air) are buoyed up by a force equal to the weight of the displaced fluid. We call this Archimedes’ principle, for the third century BC Greek who discovered it. Paul on a Plane and Knoxy even put up an equation for Archimedes’ principle, but they never mentioned Archimedes by name. I thought that that was a serious omission.

In an apparent attempt to quantify their work, Paul on a Plane and Knoxy assigned numbers to substances. For instance, they gave air a value of one and water a value of 15. However, this seemed arbitrary, and they never got around to computing anything, so this didn’t make any sense. In the conventional understanding of physics, gravity is fundamental, and buoyancy is derived from gravity. Apparently, Paul on a Plane and Knoxy suggest that buoyancy is fundamental, with gravity being a derivative of buoyancy. I suppose that one could take this approach, but until some testable predictions are made, it really isn’t a theory. Meanwhile, the conventional theory of buoyancy is a very robust theory.

Conclusion

I found this year’s meeting informative and I learned much while there. The 2019 Flat Earth International Conference is scheduled for November 14–15 in Dallas. I’ll probably decide in spring if I intend to go. I had such a good time at this meeting, I’m inclined to attend again.