Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
While astronomers and physicists widely accept the existence of dark matter today, many recent creationists oppose the existence of dark matter. There are several reasons for this opposition, some stemming from concerns that dark matter has been invoked in evolutionary scenarios. However, there is good observational evidence for dark matter. We ought not to dismiss the observational science for dark matter over fears of the misuse of dark matter in historical science.
Keywords: dark matter, baryonic matter, lighted mass, dynamic mass, MOND, MACHOs, WIMPs
Introduction
Velocity studies of clusters of galaxies in the 1930s indicated the presence of far more mass than could be accounted for by the amount of light emitted by the galaxies within the clusters. Shortly thereafter, rotation curves of individual spiral galaxies indicated the same thing may be true of galaxies in general. Both lines of evidence suggested that the preponderance of the mass of galaxies was invisible. This anomaly originally was coined missing mass, but eventually it became known as dark matter. As its name implies, dark matter gives off no light, or at least very little light.
“Normal” matter consists of atoms. Most of the mass of atoms is in the form of neutrons and protons. Physicists include protons and neutrons in a class of particles called baryons. Therefore, the technical term for “normal matter” is baryonic matter. Baryonic matter interacts via electromagnetic forces, producing light in the process. Therefore, it would be very difficult to hide a significant amount of baryonic matter from view. If the missing mass were in the form of gas or dust, the amount of missing mass required would be easily detectable. For instance, within 15 kpc1 of the center of our galaxy, the Milky Way, there is approximately 5 × 1010 solar masses of stars, 5 × 1010 solar masses of dark matter, and 7 × 109 solar masses of gas (Draine 2011, 4). This 15 kpc radius defines the limit of any significant light emission from the Milky Way, and so it encompasses virtually all the lighted mass of the Galaxy. If the dark matter component in this volume consisted of gas, then it would require a seven-fold increase in the amount of gas measured. Most of the matter in the universe consists of hydrogen. Neutral hydrogen readily reveals itself by 21-cm emission from a transition between the hyperfine levels of the hydrogen atom in the ground state. This is readily observed, and the observation of 21-cm emission forms the basis of our knowledge of the amount and distribution of neutral hydrogen gas in the Galaxy. If the dark matter of the Milky Way were in the form of neutral hydrogen, it would be detected easily, and it would overwhelm the emission from the neutral hydrogen that we do observe. Similar considerations of other elements and energy states limit the amount of gas that can exist in the interstellar medium. Astronomers have probed the interstellar medium by various means, so the gas component listed above is well-established, with no room for any substantial additional contribution. Dust mostly consists of micron-sized particles. These particles emit in the infrared between 5–600 microns, with an average temperature of 17 K (Draine 2011, 121). This, too, is readily observed and forms part of the basis of our knowledge of the distribution and composition of the dust in the interstellar medium. The combined mass of dust appears to be slightly less than one percent of the hydrogen gas component of the interstellar medium (Draine 2011, 246, 266). Hence, like gas, dust is incapable of accounting for dark matter.
Even if the missing mass were in the form of very faint stars, collectively they ought to be visible. Numerous black holes or many planet-sized objects could elude direct detection, but their presence could be deduced via gravitational lensing. Gravitational lensing occurs when a very massive object lies along the line of sight of a more distant object. The gravity of the massive object bends the light of the distant object, acting similarly to a lens, though the principle here is the bending of space-time and not refraction, as occurs with a normal lens. How the light is lensed depends upon several factors, such as how closely to the lensing object the light passes, how massive the lensing object is, and the extent of the lensed object. If dark matter consists of black holes and planet-sized objects, they would possess relative motion with respect to more distant stars, producing lensing events as they passed very close to the line of sight of the stars. The lensing would result in a brief increase in the light of the lensed stars. The data from lensing events permits modeling the properties of lensing objects, such as their masses. Observational programs to detect such objects via gravitational lensing have failed to produce them in sufficient quantity to account for the dark matter indicated by dynamic studies. Since each of these possibilities for dark matter being baryonic appear to have been eliminated, it is likely that dark matter is non-baryonic. Non-baryonic forms of dark matter might not radiate, but physicists expect that all forms of matter, including non-baryonic matter, interact gravitationally (which is the observational basis for believing dark matter exists). Much attention has been directed to determine what form dark matter may be in.
While astronomers generally accept the reality of dark matter today, this has not always been the case. For more than 30 years, astronomers generally ignored the data suggesting dark matter. The situation began to change in the 1970s as new data for dark matter accumulated. Astronomers gradually began to evaluate the data, and over the past 30 years, astronomers have come to embrace dark matter. Inclusion of dark matter in big bang models is more recent, dating to the early 1990s. Still, some scientists, primarily physicists, reject dark matter. Most attempts to explain the data apart from dark matter have concentrated on MOdified Newtonian Dynamics (MOND) (Milgrom 1983). MOND posits that our understanding of gravity being indirectly proportional to the square of distance may be in error. If the functional dependence of gravity varies from this form at great distances, such as those encountered on the scale the size of galaxies, then one may be able to explain the motions of galaxies and objects within galaxies without appealing to dark matter. While astronomers generally are more enthusiastic about dark matter than physicists are, even among physicists, the majority favors dark matter to MOND.
Despite its widespread acceptance in the scientific community, many recent creationists remain resistant to the existence of dark matter. For instance, see Davies (2010), Hartnett (2006), Oard and Sarfati (1999), and Worraker (2002). There are several reasons for this reluctance, which I shall discuss. Thus far, only one review sympathetic to dark matter has appeared in the creation literature (DeYoung 1999). There are several lines of evidence for dark matter, which I shall now discuss.
Evidence for Dark Matter
The case for dark matter goes back to the work of Fritz Zwicky in the 1930s. Zwicky (1937) measured the mass of the Coma Cluster of galaxies two ways. First, Zwicky determined the lighted mass by measuring the total light emitted by the galaxies in the cluster and multiplying by the mass-to-light ratio. The mass-to-light ratio is the mass contained within a volume of space divided by the radiation emitted from that volume. The radiation emitted by a volume of space typically is dominated by starlight. Most of the mass is in the form of stars, though there is a component from the interstellar medium, matter between the stars in the form of diffuse gas and dust. There is a huge range in stellar luminosity, but a much more modest range in stellar masses. Most stars have low mass, so low-mass stars represent the bulk of stellar mass. However, low-mass stars produce little light, so they do not contribute much to the total light emitted. On the other hand, the relatively rare high-mass stars produce a tremendous amount of light. Consequently, high-mass stars contribute little to the total mass, but their light dominates the total light from any volume of space in which they are found. Given these considerations, it is important to sample a typical volume of space when determining the mass-to-light ratio.
Fortunately, the solar neighborhood, the region of space containing stars that are closest to our sun, appears to be a good sample of our Galaxy, the Milky Way. Being so close, we have reliable distances for stars in the solar neighborhood. Knowing a star’s distance, it is easy to convert the apparent brightness of the star to an absolute brightness. Therefore, a census of the solar neighborhood yields the total light emitted from the volume contained by the solar neighborhood. We also have reliable masses for stars in the solar neighborhood. These are determined two ways. Many stars are members of binary star systems, two stars orbiting one another under the influence of their mutual gravity. Study of the motions of the stars in a binary system, along with the application of Newton’s law of gravity, permits us to determine the masses of stars. This allows us to measure directly the masses of stars in the solar neighborhood that are members of binary star systems. What of the stars in the solar neighborhood that are not members of binary star systems? Most stars lie along the main sequence of the Hertzsprung-Russell diagram (for a discussion of the main sequence and the Hertzsprung- Russell diagram, see Faulkner and DeYoung [1991]). Stars on the main sequence obey a mass-luminosity relationship, so if we know a star’s spectral type, we can infer its mass from its location on the main sequence. The stars of the solar neighborhood have been extensively studied, so all this information has been known for some time. The light-to-mass ratio of the solar neighborhood is slightly less than unity (Mihalas 1968, 64; Peebles 1993, 429). Furthermore, this mass-to-light ratio matches those deduced for the central parts of other galaxies.
Astronomers recognize two stellar populations (Faulkner 1993). The stars in the solar neighborhood are a good sample of population I stars, but what is the mass-to-light ratio of population II stars? Globular star clusters are an excellent example of population II stars. The members of globular clusters appear gravitationally bound, so study of the observed velocities of stars within a globular cluster permits measurement of the total mass of the cluster. The principle involved, Newton’s law of gravity applied to orbital motion, is identical to that used to measure the masses of stars in binary star systems. However, the technique is different. The motion of a star in its orbit will result in a Doppler shift, which we can measure spectroscopically. In general, the radial velocity (what astronomers call the velocity along our line of sight) of a star will be less than its true orbital velocity. The orbital plane will be inclined to the plane of the sky at some unknown angle between zero and 90°. This will foreshorten the velocity by the factor of sin (i), where i is the orbital inclination. However, if we measure a large sample of radial velocities, we can treat the results statistically to account for this. There is an additional small factor. The orbital velocity can be broken into two components: one along our line of sight (the radial direction) and perpendicular to our line of sight (the tangential direction). While we can readily measure the radial velocity component spectroscopically, globular clusters are too distant for any meaningful tangential velocity measurements. Via the Pythagorean theorem, the orbital velocity will be the square root of the sum of the squares of the two components. Stars observed near the center of a globular cluster will have nearly zero radial velocity and maximum tangential velocities, while stars observed near the perimeter will have nearly zero tangential velocities and maximum radial velocities. Therefore, astronomers measure the radial velocities around the perimeters of globular clusters. The crowding of the field near the center of a globular cluster makes it difficult to measure radial velocities of stars near the center anyway.
It is relatively easy to measure the total light that we receive from a globular cluster, and knowing the distance, we can express this in absolute terms. Simple division of the mass by the light reveals the mass-to-light ratio. The mass-to-light ratio of globular clusters is close to unity (Mihalas 1968, 236), and matches the population I result obtained in the solar neighborhood. With the range of stellar types well-sampled and consistent results across that range, as well as similar results from the central regions of other galaxies, astronomers have confidence that we know the mass-to-light ratio, probably well within a factor of two. There is no observational evidence that suggests the Milky Way is an atypical galaxy, so the measured mass-to-light ratio derived within the Milky Way probably is applicable to other galaxies. Therefore, Zwicky’s measurement of the lighted mass of the Coma Cluster appears reasonable.
The second method that Zwicky used to determine the mass of the Coma Cluster was to measure its dynamic mass. This method is the same as that used to measure the masses of globular star clusters. We call the mass measured this way the dynamic mass, because it is determined from motion directly due to gravity. The dynamic mass relies upon well-established physics, so it ought to be a reliable measurement of mass. Indeed, this is the method in which nearly all masses are measured, including here on earth. However, Zwicky found that the dynamic mass dwarfed the lighted mass of the Coma Cluster. He found similar results for other clusters of galaxies. Because the dynamic mass overwhelmed the lighted mass, Zwicky reasoned that the preponderance of the mass emitted little or no light, so he called it dark matter, but for decades, most astronomers referred to this as missing mass.
The ratio of dynamic mass to lighted mass varies from cluster to cluster, typically ranging between 5 and 20. However, Zwicky’s original measurements were far higher than this. There are several reasons for this. The primary factor was a serious underestimate of extragalactic distances. The distances to galaxy clusters normally are measured via the Hubble relation. For the clusters under consideration, the distance, D, is given by v/H, where v is the radial velocity and H is the Hubble constant. The early estimates of the Hubble constant were much higher than those of today. The Hubble constant and distance are inversely proportional, so a higher value for the Hubble constant results in less distance. Since the galaxies Zwicky studied were much farther away than he thought, Zwicky underestimated the brightness of the galaxies, and hence underestimated the lighted mass of the galaxies. One might be tempted to argue that if the Hubble constant were much lower, the need for dark matter would disappear. However, this would require that the Hubble constant is at most 1/5 its currently accepted value. It is extremely unlikely that our measurements of the Hubble constant today are that greatly in error. For instance, Cepheid variables play a key role in establishing the value of the Hubble constant, and it appears the Cepheid period-luminosity relation is calibrated with a few percent. Furthermore, there are other lines of evidence for dark matter that are independent of the Hubble constant.
The opportunity for the second line of evidence for dark matter came quickly. Babcock (1939) published a rotation curve of the Andromeda Galaxy (M31). A rotation curve for a galaxy is a plot of measured radial velocity versus distance from the center of the galaxy. Babcock’s Plate III is very illustrative (Fig. 1). It displays radial velocity measurements along the major axis of M31 versus distance from the center of M31. The distance is expressed in terms of an angle (minutes of arc) rather than linear distance. Knowing how far away M31 is, it is easy to convert the angular distance to linear distance. The estimates of the distance to M31 in the 1930s were much less than modern values, it is convenient for us that Babcock did not convert angular distances to linear distances. Since the measurements were along the major axis, the orbital motion is almost entirely in our line of sight, and hence the measured radial velocity is very close to the orbital velocity at each point (the measured velocities must be corrected for the angle of tilt of M31, about 15°). Above the plot is a photograph of M31 on the same angular scale. The plot of the radial velocity measurements within 20 arcminutes of the center is linear with distance from the center. This central region spans about 20% of M31’s visible radius, but it accounts for most of M31’s light. The objects here were unresolved, so Babcock’s radial velocity measurements were smoothed velocities of the unresolved center region. There generally was not enough light outside the central region of M31 to extend observations beyond the 20 arcminutes. The exceptions were five gaseous nebulae (now called HII regions). Their locations are indicated by circles on the photograph of M31. One of the five HII regions was close to the minor axis of M31, but well outside the central region. Its radial velocity was nearly identical to the radial velocity of the center of M31. These facts strongly imply that this particular HII region was in M31’s plane at great distance from the center of M31, but viewed nearly along our line of sight to M31. It lies outside of the central region of M31, because the plane of M31 is tilted about 15° out of the plane of the sky. The four remaining HII regions were close to M31’s major axis, anywhere from nearly 30 arcminutes from the center of M31 to nearly 100 arcminutes from the center. This latter HII region lies at or just beyond the visible edge of M31. Babcock plotted the radial velocities of the HII regions with ringed dots. Since the rotation curve appears symmetrical about the center, the radial velocities of the four HII regions are reflected to the other side as dotted circles.
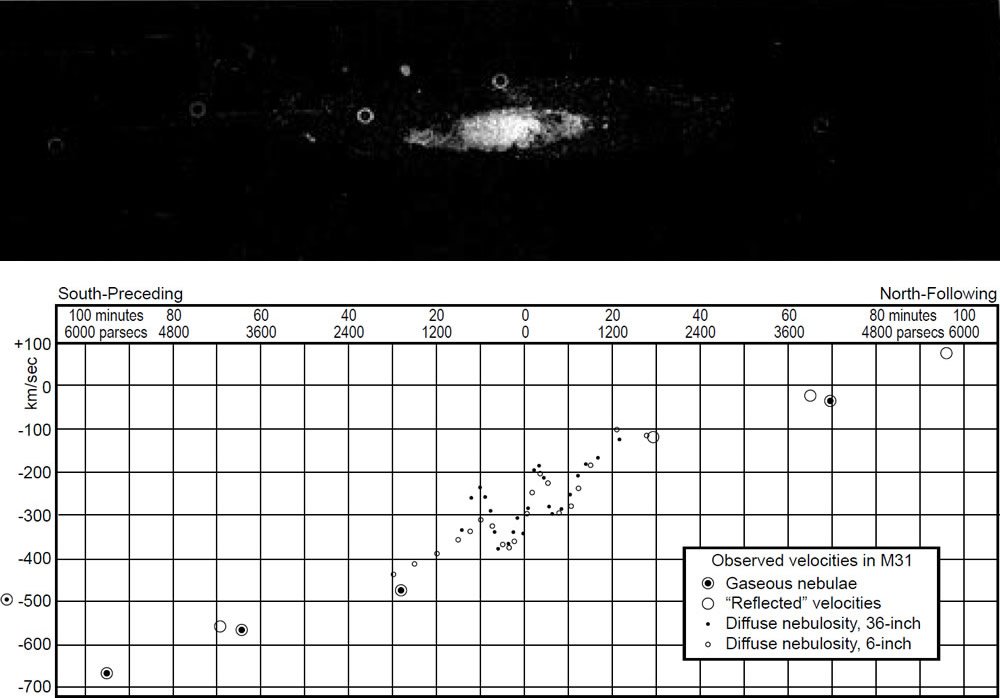
Fig. 1. The Andromeda Galaxy M31 in the photograph above, with its observed velocities plotted below. Smoothed mean velocities of the unresolved central portion are represented by small dots for observations with the Crossley reflector, and by small open circles for observation with the 6-inch mirror. In the photograph, the bright-line emission nebulosities are encircled, and their velocities, with the exception of the one on the minor axis, are plotted as ringed dots. Plot after Babcock (1939).
Outside the central region of M31, light rapidly decreases with increasing distance from the center of the galaxy. This suggests a rapid decrease in mass with increasing distance outside of the central region. Most galaxies, including M31, appear to have radial symmetry, so one would expect that the mass is radially symmetric as well. Orbital motion of any type requires centripetal acceleration given by
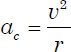
where v is the orbital velocity and r is the radius of the orbit. If the orbital motion is induced by gravity, then the centripetal acceleration is equal to the gravitational acceleration,
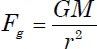
where G is the gravitational constant, and M is the mass contained within radius r. Combining these two equations,
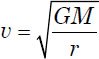
That is, orbital velocity ought to be inversely proportional to the square root of the distance. This relationship holds for the orbits of the planets. Since Kepler first described planetary motion in a correct form, this functional dependence of orbital speed with orbital distance is called Keplerian motion. Since there is some light, and hence some mass, outside of the central region of a galaxy, orbital motion outside the central region ought not be strictly Keplerian, though there ought to be a strong Keplerian component in the radial velocity as a function of distance from the center of M31 outside of the central region. However, the radial velocities of the HII regions appear to have a linear relationship with positive slope, though not as steep a slope as observations from the central region. This is a radical departure from the expected behavior.
What did this mean? Babcock summed it very well: “. . . the obvious interpretation . . . is that a very great proportion of the mass of the nebula [M31] must lie in the outer regions.” This is even though most of the light comes from the central region, where one would think that most of the matter resides. How much is the mass distribution askew? Assuming that the mass distribution is reasonably symmetrical, one can use the measured radial velocity at any position to measure the amount of mass interior to that position. Computing the interior mass at various points indicates the mass distribution as a function of distance from M31’s center. In section VI of his paper, Babcock modeled the mass distribution of M31 based upon his observations. He considered a central sphere of radius 4 arcminutes concentric with three spheroidal shells having semi-major axes of 32.1, 69.2, and 96.5 arcminutes. The four segments encompass the entire extent of the visible galaxy. Babcock tabulated his results in his Table 4 (table 1). He found a total mass-to-light ratio of about 50, far larger than what we find in the solar neighborhood. As for the mass distribution, Babcock found that only about 10% of the mass was in the central region of M31, while 90% of the mass was outside of the central region, even though most of the light from M31 emanates from the central region. This ratio is remarkably similar to more recent studies of M31 and other galaxies. Babcock did not seem disturbed by this result, for he opined that perhaps absorption in the outer regions of M31 muted its brightness there or that “new dynamical considerations” were required there. As for the first possibility, we know much more about the interstellar medium now, and it is inconceivable that absorption sufficient to cause the requisite dimming is possible. It is not clear what Babcock meant by his second possibility, though in hindsight, it sounds like MOND, a suggested alternative to dark matter. The following year, Oort (1940) found a similar result for the galaxy NGC 3115. Oort determined a mass-to-light ratio of about 250 in the outer regions of NGC 3115, compared to 62 for the outer regions of M31 that Babcock had modeled. Again, this was at great variance from near unity in the solar neighborhood. Were these two galaxies unique in having massive, dim halos?
| Shell | a=b=r | c | Vc | X | Volume | Density | Mass |
|---|---|---|---|---|---|---|---|
| 1 | 4’ | 4’ | 100 x 105cm/sec | 13.5 x 10-8 dynes | 0.170 x 1064 cm3 | 6.54 x 10-22 gm/cm3 | 1.11 x 1042 gm |
| 2 | 32.1 | 4 | 203 | 7.21 | 10.78 | 1.79 | 19.3 |
| 3 | 69.2 | 8.63 | 280 | 6.06 | 99.05 | 0.612 | 60.6 |
| 4 | 96.5 | 12.3 | 375 | 7.90 | 194 | 0.62 | 120.3 |
| 201 x 1042 gm | |||||||
Oddly, no one followed up on these strange results for three decades. It could be the intervention of the Second World War that diverted the attention of many astronomers to defense-related research for several years, and these peculiar results fell out of memory. Or perhaps the results were so far out of the realm of expectation that no one knew what to make of them, so they were consciously ignored. Today, the ratio of unseen to visible matter, about ten, coming from both radial velocity studies of galaxies and dynamical studies of galaxy clusters are remarkably similar, but, as previously discussed, Zwicky’s initial estimate was far too high. Perhaps this prevented astronomers from tying the two together, thus weakening the case for dark matter. Or perhaps a major reason no one pursued this interesting topic for so long was limitations of the instruments then available. Because spectroscopy requires dispersion of light, it is a very inefficient use of light. The individual objects in other galaxies that must be observed, such as HII regions, are extremely faint. Therefore, the observations required to conduct the necessary radial velocity studies of distant galaxies require many hours, even on the largest telescopes in the world. And the two galaxies that Babcock and Oort observed are among the closest, and hence brightest appearing, galaxies. By 1970, an increased number in large telescopes, along with advancements in detector technology made the necessary observations for this research more feasible.
Relying upon recent observations of others, Ostriker, Peebles, and Yahil (1974) called attention to the fact that the measured mass distributions of galaxies are roughly linear with distance from their centers, even though the light distributions of the galaxies converge to some limiting value. They commented that this has led to an underestimate of galaxy masses by a factor of 10 or more, which had profound cosmological implications. This also meant that massive halos surrounded galaxies. They estimated that the required mass-to-light ratio of the halos of galaxies was approximately 50–100. Again, this is very similar to the results of Babcock and Oort decades earlier. Ostriker, Peebles, and Yahil (1974) suggested that the massive halos might be in the form of very faint stars.
During the 1970s, Vera Rubin and Kent Ford took advantage of improved astronomical instrumentation to collaborate on a series of papers that produced new data that indicated the need for massive halos. For instance, Rubin and Ford (1970) greatly improved upon Babcock’s rotation curve of M31 by obtaining spectra of 67 HII regions 3–24 kpc from the center of M31. They primarily used the Hα emission line to measure radial velocities of the HII regions. Furthermore, they observed the NII emission line at 6583 Å to probe the 3 kpc central region. They also measured radial velocities of associations of O and B stars. Their Figure 11 (reproduced here as Fig. 2) showed various fits to the combined data. In the central region, they found a steep linear increase of velocity with distance out to 400 pc, followed by a deep minimum around 2 kpc, and a recovery to high values near 3 kpc, blending with the HII region data there. This form is common in rotation curves of spiral galaxies. In another paper, Rubin, Ford, and Thonnard (1978) presented rotation curves outside the central regions of 10 high-luminosity spiral galaxies. All rotation curves were approximately flat outside the central regions, indicating almost no dependence upon distance there. The authors were guarded in their conclusion about the necessity of massive halos, but just two years later they were bolder. Rubin, Ford, and Thonnard (1980) presented rotation curves outside of the central regions of 21 Sc galaxies spanning a wide range of sizes. Most of the rotation curves were not only linear, but increasing, at large radius. In their conclusion, they wrote:
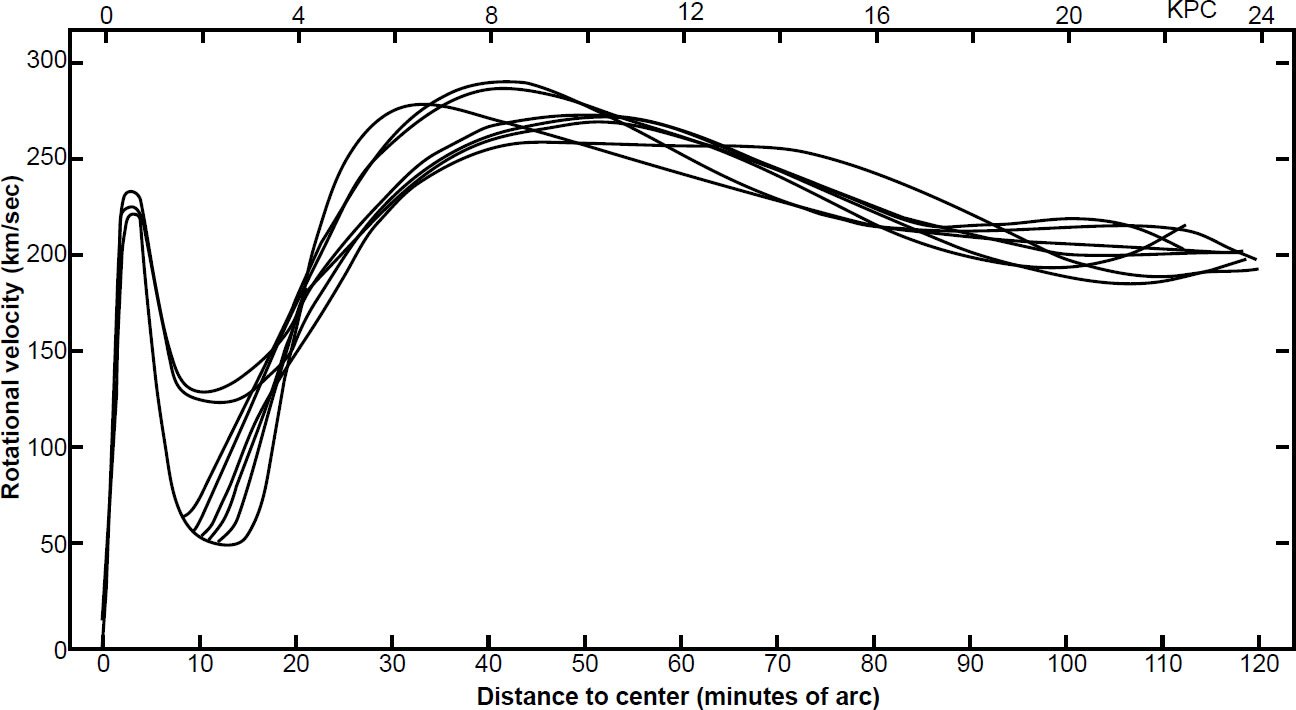
Fig. 2. Measured radial velocities of associations of O and B stars in galaxies (after Ostriker, Peebles, and Yahil 1974).
This form for the rotation curves implies that the mass is not centrally condensed, but that significant mass is located at large R. The integral mass is increasing at least as fast as R. The mass is not converging to a limiting mass at the edge of the optical image. The conclusion is inescapable that non-luminous matter exists beyond the optical galaxy. (emphasis added)
Data collection that confirm this conclusion has continued since. It took the astronomy community considerable time to digest and then accept this conclusion. It did not do so lightly. The case for dark matter halos from rotation curves of galaxies is well established. However, there are other lines of evidence for dark matter.
While Rubin and Ford worked with spiral galaxies, Faber and Jackson (1976) studied velocity dispersions of elliptical galaxies to infer mass-to-light ratios. In their study, they found that the mass-to-light ratio of 25 elliptical and S0 galaxies averaged 7. This was lower than previous studies, but still appreciably greater than the locally determined value of near unity. While it appears now that most galaxies of all types have appreciable components of dark matter, there are some exceptions. For instance, the elliptical galaxy NGC 3379 appears to have little or no dark matter (Ciardullo, Jacoby, and Dejonghe 1993).
In recent years, astronomers have discovered many previously unknown galaxies with very low surface brightness.2 These galaxies had escaped detection because of their lack of light, apparently due to these galaxies containing so few stars. Probing the dynamical behavior of these galaxies has revealed that dark matter dominates their mass. For instance, a recent study (von Dokkum et al. 2016) found that inner region of the ultra-diffuse galaxy Dragonfly 44 has a mass-to-light ratio of about 50, and that the galaxy mass is 98% dark matter.
Gravitational lensing by clusters of galaxies provide another line of evidence for dark matter. As previously mentioned, gravitational lensing is a consequence of gravity predicted by the theory of general relativity, occurring when a distant object is aligned with a very massive, closer object. More specifically, a cluster of galaxies is the massive object that lenses the light from a more distant galaxy or quasar. The way the distant object is lensed depends upon the amount and distribution of matter in the galaxy cluster, so modeling the observations reveals both the mass and its distribution in the galaxy cluster. There now are many such examples of gravitational lensing, and their results indicate the same overabundance of dark matter over lighted matter that other lines of evidence indicate.
One of the best examples of evidence of dark matter is the galaxy cluster 1E0657-558 (Clowe, Gonzalez, and Markevitch 2008), the so-called “Bullet Cluster” (Fig. 3). This cluster is interacting, meaning that it is a collision of two clusters. Most of the baryonic matter in the cluster is in the form of gas that emits x-rays. The stars of either cluster have small cross-sectional areas, so they passed through one another with only slight deflections in the motions of some of the stars. However, being large diffuse objects, the gas clouds have large cross-sections and collided. The effect of the collision was to stall the gas clouds, causing them to lag the motions of the star involved. Consequently, the x-ray and visible light emissions from the cluster do not coincide. However, the gravitational lensing appears to be centered on the optical portion, not the x-ray portion. This is significant, because of the primary competitor to dark matter is MOND, but MOND would require that gravitationally lensed images be centered on the bulk of the baryonic matter, which corresponds to the region where the x-rays come from, not the visible light. Thus, this is evidence that MOND is not correct, though supporters of MOND disagree and have concocted explanations of how MOND may explain these results. A similar argument applies for the merging galaxy cluster MACS J0025.4-1222 (Bradač et al. 2008). Those who doubt dark matter’s existence have responded (e.g. Angus, Famaey, and Zhao 2006; Hartnett 2006). However, I find their responses unconvincing, because the responses amount to adjustments to MOND to fit the data.

Fig. 3. Bullet Cluster of galaxies 1E0657-558 (Clowe, Gonzalez, and Markevitch 2008).
What is Dark Matter?
The identity of dark matter remains one of the enduring mysteries of modern astronomy and physics. The simplest answer would be that dark matter is baryonic, albeit in objects that heretofore were thought to be only a minor contributor to the total mass. Could it be in the form of dust or gas? Unless their temperature is at absolute zero (something that the third law of thermodynamics would seem to preclude), dust and gas must radiate. This is particularly true of clouds of dust and gas. Emission from dust and gas in the disks of galaxies is readily detectable, even though the total mass contributed by both is relatively small compared to stellar mass. Therefore, the far more massive halos of dust or gas required to explain dark matter would be obvious. Since they are not, we can eliminate dark matter being in the form of dust or gas.
If dark matter consists of baryonic matter in massive, yet small objects, then it might escape easy detection. This identification of dark matter is known as MACHOs, with MACHO standing for MAssive Compact Halo Object. MACHOs would include black holes, white dwarfs, brown dwarfs, and planets. Brown dwarfs are spheres of hot gas that have mass less than 7% of the sun’s mass. Above this threshold, there is sufficient temperature in a star’s core to sustain nuclear reactions to power the star. However, below this threshold, there is not, so objects having less than 7% the sun’s mass technically are not stars, though they appear like stars at or just above the mass threshold. Astronomers now think of stars and planets being on a continuum, with brown dwarfs being the transition point between stars and planets. When Ostriker, Peebles, and Yahil (1974) suggested that dark matter might be in the form of very faint stars, they were suggesting what later became known as MACHOs (keep in mind that at the time, astronomers did not yet acknowledge the possibility of brown dwarfs).
It would be difficult to detect MACHOs by the radiation they emit, but we can detect them via small gravitational lensing events called microlensing. If a MACHO were to pass directly between us and a distant star, gravitational lensing briefly would intensify the star’s light. One extensive microlensing search was that of Alcock et al. (2000). Over a nearly six-year period, this team regularly monitored 11.9 million stars in the Large Magellanic Cloud (LMC), a satellite galaxy of the Milky Way. We view the LMC at low galactic latitude through the galactic halo, so if MACHOs comprise a significant portion of dark matter in the galactic halo, we would expect at least a few microlensing events as those bodies orbited the galaxy. They found more than a dozen microlensing events, slightly more than we would expect from faint stars known to be in the galactic halo. This result is consistent with at least some MACHOs, but not nearly enough to account for dark matter known to exist. However, another study (Tisserand et al. 2007) failed to find enough microlensing events consistent with any MACHOs. This study lasted nearly seven years, monitoring nearly as many stars as the other study, but in the Small Magellanic Cloud (SMC), as well as the LMC. These results are typical of MACHO study—either no evidence of MACHOs, or not nearly enough to account for dark matter.
If dark matter is not baryonic, then what possible nonbaryonic forms might it be? In a clever word play response to the name MACHO, one nonbaryonic theory about the identity of dark matter is WIMPS, standing for Weakly Interacting Massive Particles. The existence of WIMPs is allowed under an extension of the standard model of elementary particles via supersymmetry (though supersymmetry theory yet has no evidence). The exact properties of WIMPs are unknown, but if these particles exist, they ought to interact very weakly with baryonic matter. The inferred distribution of dark matter in our galaxy shows a considerable contribution in our location, so as we move through space, we ought to pass through much dark matter. If dark matter is made of WIMPs, then we could directly detect the rare interactions between WIMPs and ordinary matter. Several experiments have operated and continue to operate based upon this possibility of direct dark matter detection. The two most famous of these is LUX (Large Underground Xenon) experiment a mile below the earth’s surface in the Homestake Gold Mine in Lead, South Dakota and XENON, at the Gran Sasso lab in Italy. So far, there have been no unambiguous detections of WIMPs, though this remains the dominant hypothesis to explain dark matter. Some creationists have misinterpreted these null results as evidence that dark matter does not exist. However, this is not true—the null results merely indicate that WIMPS, a particular type of dark matter, is unlikely to exist.
At least two other particles have been suggested as possible dark matter candidates, axions and sterile neutrinos. Both are hypothetical particles that have not yet been found, and so may not exist at all. They do not enjoy broad support.
Some physicists do not think that dark matter exists. How do they explain the evidence for dark matter? They suggest modification of Newton’s law of gravity (MOND). MOND suggests that the inverse square law of gravity works over distances on the size of the solar system, but that over much larger distances, such as galactic sizes, the inverse square law is a poor approximation. That is, there is an additional term in how gravity works that does not show up on the scale of the solar system, but does on larger scales. This is a radical solution to the problem, more radical than the existence of heretofore unknown matter in the estimate of most physicists. Nor is this the first time that MOND has been proposed. In the eighteenth century, there was considerable debate about the precession of the moon’s orbit. Despite the tremendous success of Newton’s law of gravity in explaining orbital motion in general, Newton failed to account for the moon’s orbital precession, getting a precession period twice that of the actual value. Three mathematicians who took up the challenge are of note: Alexis Clairaut, Jean le Rond d’Alembert, and Leonhard Euler (Bodenmann 2010). All three men considered modification of the inverse square law, though Euler was the most insistent on that solution. Clairaut eventually solved the problem. The difficulty had been how to handle the n-body problem. Simple orbital and even tidal force interactions are 2-body problems, problems that are easily solved in closed form. However, once a third body was introduced, as with precession of the moon’s orbit, the problem defied simple algebraic solution. It was not until Clairaut’s technique of handling the n-body problem was the matter of the moon’s orbital precession resolved. There was no dark matter invoked here, but an eighteenth-century version of MOND proved not to be necessary.
Nor is the invocation of dark matter a novel concept. In 1781, William Herschel discovered Uranus, the first planet discovered since ancient times, and the first planet not generally visible to the naked eye. Six decades later, Uranus had completed a nearly entire orbit of the sun since its discovery. It was not following precisely the orbit that Newtonian physics dictated that it should. The discrepancies were small, but required explanation. The simplest explanation was that there was another planet orbiting the sun beyond Uranus whose gravity was slightly perturbing Uranus in its orbit. From the observed orbital discrepancies, it was possible to compute the hypothetical new planet’s position, something that the mathematicians Urbain Le Verrier and Jonh Couch Adams independently did. When Johann Gottfried Galle at the Berlin Observatory checked Le Verrier’s predicted position, he found the planet Neptune. Prior to Galle’s seeing Neptune, Neptune’s existence had been inferred from its gravitational force, essentially making it a nineteenth century version of dark matter.
Or consider the discovery of Saturn’s shepherd satellites. In 1979, the Pioneer 11 probe discovered the F Ring, an outermost ring of Saturn. The following year, the Voyager 1 probe showed that the F Ring had a kinked structure, resembling braiding. This was a most unanticipated result, and it sent dynamicists scrambling to explain it. The best solution quickly came—the braiding could be explained easily if there were two small satellites just inside and outside of the F Ring perturbing the ring particles. With a prediction of the positions of the yet unseen (and hence dark matter) satellites, Voyager 1’s camera captured images of both satellites, now called shepherd satellites. The inner shepherd satellite was named Prometheus, while the outer one was called Pandora. While the term shepherd satellite originally applied to these two bodies, astronomers soon found other shepherd satellites responsible for other oddities in Saturn’s rings, as well as the three other ringed planets (Jupiter, Uranus, and Neptune). The existence of all these satellites were inferred prior to their discovery, essentially making them dark matter until they were spotted.
Or consider the history of our understanding of the neutrino. By 1930, physicists faced a crisis. Experimental results indicated that beta decay (the emission of an electron or its antiparticle from an atomic nucleus) violated conservation of momentum and energy. One could have hypothesized a sort of MOND which allowed such a thing for beta decay, but that would have been a radical solution. Indeed, Niels Bohr proposed that conservation of energy was true only in a statistical sense, permitting violation of conservation of energy with any particular beta decay. Instead, Wolfgang Pauli proposed that the atomic nucleus contained additional neutrally charged particles that were emitted from atomic nuclei along with the electron or positron during beta decay. By 1934, Enrico Fermi altered Pauli’s suggestion (now calling the particles neutrinos), and theorized that neutrinos were produced at the time of beta decay. Physicists came to accept Fermi’s explanation, though it was more than 20 years before there was any direct confirmation of the neutrino’s existence. Since neutrinos do not interact electromagnetically, they remain a type of dark matter today, for they do not emit light.
To be fair, in the history of astronomy there is an example of MOND over (dark) matter. By the nineteenth century, there was a noticeable discrepancy in the observed precession of Mercury’s orbit around the sun and the predicted precession. Some astronomers attributed the discrepancy to perturbations from the gravity of a small, previously unknown planet, Vulcan, orbiting very close to the sun (making Vulcan hypothetical dark matter). However, extensive searches for Vulcan failed. It was not until the publication of Albert Einstein’s theory of general relativity a century ago that the discrepancy was explained, and this was one of the first confirmations of general relativity. Since general relativity is a modification of Newtonian gravity, this amounts to a form of MOND. While we cannot rule out MOND, it is a far more radical explanation for the data in question than dark matter is.
Why Do So Many Creationists Reject Dark Matter?
As indicated in the Introduction, within the biblical creation movement, there is much resistance to the possibility of dark matter. There are several likely reasons for this. One reason is that the motions of galaxies within clusters have been used as evidence of recent origin (Slusher 1980, 7–14), and there may be reluctance to let that go. The computation of dynamic mass was based upon the assumption that the galaxies within clusters are gravitationally bound. However, if the lighted mass is a truer measure of the mass of galaxy clusters, then the clusters are not gravitationally bound. The motions of the individual galaxies greatly exceed the escape velocity from the cluster as determined from the lighted mass, so galaxy clusters are rapidly dispersing. The time frame of the dispersal of clusters of galaxies is millions of years, far shorter than the supposed billions of years age of the universe and the clusters of galaxies that it contains. If data from clusters of galaxies remained the sole evidence for dark matter, this might have been a viable interpretation, but once rotation curves of galaxies provided an independent line of evidence for dark matter, the supposed breakup times of galaxy clusters appeared less attractive. One could argue, as Davies (2010) did, that the outer regions of galaxies are not in dynamical equilibrium, but that this appears to be grasping at straws. And it is inconsistent. Creationists generally have acknowledged that God created much of universe in dynamical equilibrium as a sort of design argument, but it appears that some creationists are willing to abandon this design argument to salvage an argument for recent origin based upon the supposed breakup of clusters of galaxies.
Once astronomers became convinced of the reality of dark matter, it did not take long for cosmologists to take note. Most cosmological models are based upon the assumption that gravity is the dominant force in the universe. Therefore, it is important for cosmologists to have a proper understanding of the amount of matter in the universe. If dark matter is the dominant component of mass in the universe, then it must be factored into cosmological models. Hence, since the early 1990s, big bang models generally have included dark matter. This has allowed cosmologists to use dark matter to solve problems within their models, and dark matter has been invoked to explain other questions, such as the formation of galaxies and the persistence of spiral structure in galaxies. In recent years, much of the discussion of dark matter has been in these contexts rather than the observational data that led astronomers to deduce the existence of dark matter in the first place. This perceived close connection between dark matter and evolutionary ideas of astronomy and cosmology probably has been the prime motivation for many creationists who oppose dark matter (Oard and Sarfati 1999). Consider the words of Hartnett (2006):
It seems that dark matter is necessary to prop-up the failing paradigm of the Friedmann cosmologies commonly believed by many to describe not only the structure but also the true (‘big bang’) beginning of the universe. . . . However, to get the theory to work, a universe comprising 22% dark matter is an absolute must. Therefore, it has become now an all-out battle to prove that the dark matter sceptics (like me), who dispute the existence of the stuff, are wrong.
Many arguments for dark matter include data from the cosmic microwave background (CMB) (Hinshaw et al. 2009). Indeed, in recent years there has been a dramatic increase in discussion of dark matter within the big bang model, so it is easy to understand why many people may erroneously think that the big bang model is the sole or at least primary reason for the widespread acceptance of dark matter today. However, this overlooks several important points. The big bang has been the dominant cosmogony for a half century, far longer than dark matter has been accepted. It was not until the 1990s that dark matter was commonly incorporated into big bang models. If dark matter is so integral to making the big bang model work, how did the model come to dominate the field of cosmology for the first 25 years without dark matter? The answer is that there is no single big bang model. Rather, it is a basic concept that has been altered tremendously over the years as new challenges emerge.
The dominant version of the big bang today is the ΛCDM (or Lambda Cold Dark Matter) model, referring to the inclusion of dark energy and slow-moving dark matter, but this has been the dominant model only since about the year 2000. Cosmologists use the ΛCDM model to interpret the CMB, making the results model-dependent. The details of observations of the CMB supposedly yield evidence for dark matter, but if the model is changed, the evidence for dark matter from the CMB data could disappear. Once astronomers and cosmologists came to accept the reality of dark matter, it became another parameter to adjust to fit to the data. It also became a lifeline to solve problems with the big bang model. For instance, for most of a century there has been a predilection in cosmology for a universe that is flat. There are various ways to achieve this, but within the constraints of today’s models, much dark matter is required. But there is no reason the universe must be flat, so dark matter is not required for this except to bolster a bias for a flat universe. Another factor is additional mass is required to bring concordance between predictions of primordial nucleosynthesis of the lighter elements and the measured abundances of those elements. Currently, only significant dark matter appears to be able to do this. However, claims of the supposed match between theoretical predictions of primordial big bang nucleosynthesis and measured abundances of the lighter elements predate the inclusion of dark matter into big bang models. For instance, Ross (1989, 87–88) made this claim prior to the inclusion of dark matter into big bang models. Clearly, if dark matter were shown not to exist, the big bang model can could be altered once again to bring theory and data back into agreement.
While it may appear to the casual observer that cosmologists invented dark matter in a desperate attempt to salvage the big bang model, the history of our understanding of dark matter is very different. Astronomers and cosmologists alike strongly resisted the existence of dark matter. It was not until after a tremendous amount of data accumulated indicating that dark matter existed in large quantities that astronomers and cosmologists reluctantly accepted it. It was only after this acceptance that cosmologists realized that dark matter could solve difficulties with the big bang model. The big bang model was popular among cosmologists long before the widespread acceptance of dark matter. It is likely that the big bang model would survive if tomorrow all physicists and astronomers abandoned belief in dark matter. The big bang model simply would be altered once again. Therefore, big bang model does not rely upon the existence of dark matter.
If dark matter is not real, then how might we explain the data that suggest its existence? The most promising solution is MOND. However, in their haste to distance themselves from dark matter and to embrace MOND, many creationists have failed to anticipate the next step. The big bang is a very plastic model—it has been adapted countless times as the need has arisen. MOND very easily could be incorporated into the big bang and used as a rescuing device to solve difficulties with the model much as dark matter has. If the situation were reversed and MOND were the preferred solution to the data, I expect that this would be exactly the case. Then many creationists would be doubting MOND and calling for dark matter.
Conclusion
There is strong observational evidence for dark matter. Yet, many biblical creationists remain skeptical of it. This skepticism appears to be based upon a misunderstanding of the reasons for belief in dark matter. Contrary to popular misconception, dark matter is not a rescuing device for the big bang model. It is true that dark matter is used to manipulate the big bang model, but that merely is because there is good evidence that dark matter exists and that the big bang suffers from problems that need fixes. The big bang was the dominant cosmogony for years before dark matter came to be accepted, so it is clear that the big bang model is not nearly as dependent upon dark matter than many creationists seem to think. If dark matter suddenly fell out of favor, all that it would eliminate is the current version of the big bang model. Soon, a new version would arise to take its place. Therefore, it is misguided to believe that denial of dark matter is a sort of silver bullet that would destroy the big bang model. Absent dark matter, the big bang model, in a different form, likely would survive.
This is a good example of the differences between what many creationists call operational science and historical science. The evidence for dark matter is within the realm of observational science; the big bang model is within the realm of historical science. We creationists claim to believe in the superiority of operational science over historical science. However, in the case of dark matter, far too many creationists have allowed pronouncements coming from ideas of historical science that they do not even agree with to overshadow those of operational science.
Physics is a well-developed science. Consequently, we know much about the nature of matter. Yet, we apparently do not know what most of the matter in the universe is. Dark matter probably is in a form that we have not yet contemplated. I find this humbling. It indicates that the Creation is far more fascinating that we can imagine, with mysteries yet to be discovered. Truly, we have a marvelous Creator. I encourage creationists to embrace the possibility that dark matter is real.
References
Alcock, C., R. A. Allsman, D. R. Alves, T. S. Axelrod, A. C. Becker, D. P. Bennett, K. H. Cook, et al. 2000. “The MACHO Project: Microlensing Results from 5.7 Years of Large Magellanic Cloud Observations.” Astrophysical Journal 542 (1): 281–307.
Angus, G. W., B. Famaey, and H. S Zhao. 2006. “Can MOND Take a Bullet? Analytical Comparisons of Three Versions of MOND Beyond Spherical Symmetry.” Monthly Notices of the Royal Astronomical Society 371 (1): 138–146.
Babcock, H. W. 1939. “The Rotation of the Andromeda Nebula.” Lick Observatory Bulletin 498: 41–51.
Bodenmann, S. 2010. “The 18th Century Battle over Lunar Motion.” Physics Today 63 (1): 27–32.
Bradač, M., S. W. Allen, T. Treu, H. Ebeling, R. Massey, R. G. Morris, A. von der Linden, and D. Applegate. 2008. “Revealing the Properties of Dark Matter in the Merging Cluster MACS J0025.4-1222.” Astrophysical Journal 687 (2): 959–967.
Ciardullo, R., G. H. Jacoby, and H. B. Dejonghe. 1993. “The Radial Velocities of Planetary Nebulae in NGC 3379.” Astrophysical Journal, Part 1 414 (2): 454–462.
Clowe, D., A. Gonzalez, and M. Markevitch. 2008. “Weak-Lensing Mass Reconstruction of the Interacting Cluster 1E0657-558: Direct Evidence for the Existence of Dark Matter.” Astrophysical Journal 604 (2): 596–603.
Davies, K. 2010. “Matching the Age of a Galaxy with its Rotation Velocity Profile.” Creation Research Society Quarterly 46: 233.
DeYoung, D. B. 1999. “Dark Matter.” Creation Research Society Quarterly 36 (4): 177–182.
Draine, B. T. 2011. Physics of the Interstellar and Intergalactic Medium. Princeton, New Jersey: Princeton University Press.
Faber, S. M., and R. E. Jackson. 1976. “Velocity Dispersions and Mass-to-Light Ratios for Elliptical Galaxies.” Astrophysical Journal 204: 668–683.
Faulkner, D. R. 1993. “The Role of Stellar Population Types in the Discussion of Stellar Evolution.” Creation Research Society Quarterly 30 (1): 8–11.
Faulkner, D. R., and D. B. DeYoung. 1991. “Toward a Creationist Astronomy.” Creation Research Society Quarterly 28 (3): 87–92.
Hartnett, J. 2006. “Has ‘Dark Matter’ Really Been Proven? Clarifying the Clamour of Claims from Colliding Clusters.” Journal of Creation 20 (3): 6–7.
Hinshaw, G., J. L. Weiland, R. S. Hill, N. Odegard, D. Larson, C. L. Bennett, J. Dunkley, et al. 2009. “Five-Year Wilkinson Microwave Anisotropy Probe Observations: Data Processing, Sky Maps, and Basic Results.” Astrophysical Journal Supplement Series 180: 225–245.
Mihalas, D., and P. M. Routly. 1968 Galactic Astronomy. San Francisco, California: W. H. Freeman.
Milgrom, M. 1983. “A Modification of the Newtonian Dynamics as a Possible Alternative to the Hidden Mass Hypothesis.” Astrophysical Journal, Part 1 270: 365–370.
Oard, M. J., and J. Sarfati. 1999. “No Dark Matter Found in the Milky Way.” Creation Ex Nihilo Technical Journal 13 (1): 3–4.
Oort, J. H. 1940. “Some Problems Concerning the Structure and Dynamics of the Galactic System and the Elliptical Nebulae NGC 2115 and 4494.” Astrophysical Journal 91 (3): 273–306.
Ostriker, J. P., P. J. E. Peebles, and A. Yahil. 1974. “The Size and Mass of Galaxies, and the Mass of the Universe.” Astrophysical Journal (Letters) 193: L1–L4.
Peebles, P. J. E. 1993. Principles of Physical Cosmology. Princeton, New Jersey: Princeton University Press.
Ross, H. 1989. The Fingerprint of God: Recent Scientific Discoveries Reveal the Unmistakable Identity of the Creator. Orange, California: Promise Publishing.
Rubin, V. C., and W. K. Ford. 1970. “Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions.” Astrophysical Journal 159: 379–403.
Rubin, V. C., W. K. Ford, and N. Thonnard. 1978. “Extended Rotation Curves of High-Luminosity Spiral Galaxies. IV. Systematic Dynamical Properties, Sa→Sc.” Astrophysical Journal (Letters) 225: L107–L111.
Rubin, V. C., W. K. Ford, and N. Thonnard. 1980. “Rotational Properties of 21 Sc Galaxies with a Large Range of Luminosities and Radii, from NGC 4605 (R = 4 kpc) to UGC 2885 (R = 122 kpc).” Astrophysical Journal 238: 471–487.
Slusher, H. S. 1980. The Age of the Cosmos. ICR Technical Monograph No. 9. San Diego, California: Institute for Creation Research.
Tisserand, P., L. Le Guillou, C. Afonso, J. N. Albert, J. Andersen, R. Ansari, E. Aubourg, et al. 2007. “Limits on the Macho Content of the Galactic Halo from the EROS-2 Survey of the Magellanic Clouds.” Astronomy and Astrophysics 469: 387–404.
van Dokkum, P., R. Abraham, J. Brodie, C. Conroy, S. Danieli, A. Merritt, L. Mowla, A. Romanowksy, and J. Zhang. 2016. “A High Stellar Velocity Dispersion and ~100 Globular Clusters for the Ultra-Diffuse Galaxy Dragonfly 44.” Astrophysical Journal (Letters) 828: L6.
Worraker, B. 2002. “MOND over Dark Matter?” TJ 16 (3): 11–14.
Zwicky, F. 1937. “On the Masses of Nebulae and of Clusters of Nebulae.” Astrophysical Journal 86: 217–246.












