Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
Over the last 80 years numerous determinations have been made of the 147Sm half-life. The determinations since 1960 have converged on close agreement between the two primary determination techniques used in direct physical counting experiments—ionization chambers and liquid scintillation counters, and with radioisotope age comparisons using two meteorites. Thus the 147Sm half-life value of 106 ± 0.8 Byr has now been adopted for standard use by the uniformitarian geological community. This value is based on the weighted average of four direct counting determinations in the period 1961–1970 and the recalibration in the 1970s of Sm-Nd model ages of two meteorites by forcing them (essentially by circular reasoning) to agree with their Pb-Pb isochron and model ages. However, direct counting experiments in 2003 determined the 147Sm half-life value was 10% or more longer at 117 ± 2 Byr. This was achieved by using four standard Sm solutions with internal α-radioactive standards in 19 alpha spectrometer and 24 ionization chamber determinations, making it the most thorough and comprehensive effort to determine the 147Sm half-life. The thinner counting sources used, while resulting in low α-activities being measured, greatly reduced the counting uncertainty due to self-absorption of the emitted α-particles. Although rejected or ignored, this 117 ± 2 Byr value for the 147Sm half-life, which agrees with some earlier determinations, may well be highly significant and more reliable than the adopted value. Yet, in spite of the many experiments directly measuring 147Sm decay, preference has been given to the half-life value of 106 ± 0.8 Byr determined by forcing the Sm-Nd data to agree with Pb-Pb dates. But many unprovable assumptions are also involved, not the least being that the radioisotope systems closed at the same time and subsequently remained closed. Furthermore, even this “gold standard” has unresolved uncertainties due to the U decay constants being imprecisely known, and to measured variations of the 238U/235U ratio in terrestrial rocks and minerals and in meteorites. Both of these factors are so critical to the U-Pb method, as well as the additional factor of knowing the initial concentrations of the daughter and index isotopes, so it should not be used as a standard to determine other decay constants. In any case, the determined half-life of 147Sm has been shown to be dependent on the thicknesses of the Sm counting source and the detector. There is also evidence decay rates of the radioisotopes used for rock dating have not been constant in the past. This only serves to emphasize that if the Sm-Nd dating method has been calibrated against the U-Pb “gold standard” with all its attendant uncertainties, then it cannot be absolute, and therefore it cannot be used to reject the young-earth creationist timescale. Indeed, current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
Keywords: radioisotope dating, decay constants, half-lives, samarium-147, 147Sm, α decay, direct counting, emulsions, liquid scintillation counters, ionization chambers, surface-barrier detectors, Geiger counter, counting efficiencies, geological comparisons, meteorites, U-Pb “gold standard”, 238U/235U ratio
Introduction
Radioisotope dating of rocks and meteorites is perhaps the most potent claimed proof for the supposed old age of the earth and the solar system. The absolute ages provided by the radioisotope dating methods provide an apparent aura of certainty to the claimed millions and billions of years for formation of the earth’s rocks. Many in both the scientific community and the general public around the world thus remain convinced of the earth’s claimed great antiquity.
However, accurate radioisotopic age determinations require that the decay constants of the respective parent radionuclides be accurately known and constant in time. Ideally, the uncertainty of the decay constants should be negligible compared to, or at least be commensurate with, the analytical uncertainties of the mass spectrometer measurements of isotopic ratios entering the radioisotope age calculations (Begemann et al. 2001). Clearly, based on the ongoing discussion in the conventional literature this is not the case at present. The stunning improvements in the performance of mass spectrometers during the past four or so decades, starting with the landmark paper by Wasserburg et al. (1969), have not been accompanied by any comparable improvement in the accuracy of the decay constants (Begemann et al. 2001; Steiger and Jäger 1977), in spite of ongoing attempts (Miller 2012). The uncertainties associated with most direct half-life determinations are, in most cases, still at the 1% level, which is still significantly better than any radioisotope method for determining the ages of rock formations. However, even uncertainties of only 1% in the half-lives lead to very significant discrepancies in the derived radioisotope ages. The recognition of an urgent need to improve the situation is not new (for example, Min et al. 2000; Renne, Karner, and Ludwig 1998). It continues to be mentioned, at one time or another, by every group active in geo- or cosmochronology (Schmitz 2012). This is a key issue especially for very long half-life radioisotopes due to the very slow accumulation of decay particle counting data, because the statistical error is equal to the square root of the total decay particle counts.
From a creationist perspective, the 1997–2005 RATE (Radioisotopes and the Age of The Earth) project successfully made progress in documenting some of the pitfalls in the radioisotope dating methods, and especially in demonstrating that radioisotope decay rates may not have always been constant at today’s measured rates (Vardiman, Snelling, and Chaffin 2000, 2005). Yet much research effort remains to be done to make further inroads into not only uncovering the flaws intrinsic to these long-age dating methods, but towards a thorough understanding of radioisotopes and their decay during the earth’s history within a biblical creationist framework.
One crucial area the RATE project did not touch on was the issue of how reliable have been the determinations of the radioisotope decay rates, which are so crucial for calibrating these dating “clocks.” Indeed, before this present series of papers (Snelling 2014a, 2014b, 2015) there have not been any attempts in the creationist literature to review how the half-lives of the parent radioisotopes used in long-age geological dating have been determined and to collate their determinations so as to discuss the accuracy of their currently accepted values. After all, accurate radioisotope age determinations depend on accurate determinations of the decay constants or half-lives of the respective parent radioisotopes. The reliability of the other two assumptions these absolute dating methods rely on, that is, the starting conditions and no contamination of closed systems, are unprovable. Yet these can supposedly be circumvented somewhat via the isochron technique, because it is independent of the starting conditions and is sensitive to revealing any contamination, which is still significantly better than any radioisotope method for determining the ages of rock formations. Data points that do not fit on the isochron are simply ignored because their values are regarded as due to contamination. Yet there is also no reliable way of determining the difference between isochrons and mixing lines. That this is common practice is illustrated with numerous examples from the literature by Dickin (2005) and Faure and Mensing (2005). On the other hand, it could be argued that this discarding of data points which do not fit the isochron is arbitrary and therefore is not good science, because it is merely assumed the “aberrant” values are due to contamination rather than that being proven to be so. Indeed, in order to discard such outliers in any data set, one must establish a reason for discarding those data points which cannot be reasonably questioned.
In order to rectify this deficiency, Snelling (2014a, 2014b, 2015) has documented the methodology behind and history of determining the decay constants and half-lives of the parent radioisotopes 87Rb, 176Lu, and 187Re used as the basis for the Rb-Sr, Lu-Hf, and Re-Os long-age dating methods respectively. He showed that there is still some uncertainty in what the values for these measures of the 87Rb and 176Lu decay rates should be, in contrast to the apparent agreement on the 187Re decay rate. This uncertainty is especially prominent in determinations of the 176Lu decay rate by physical direct counting experiments. Furthermore, the determined values of the 87Rb decay rate differ when Rb-Sr ages are calibrated against the U-Pb ages of either the same terrestrial minerals and rocks or the same meteorites and lunar rocks. Ironically it is the slow decay rate of isotopes such as 87Rb used for deep time dating that makes a precise measurement of that decay rate so difficult. Thus it could be argued that direct measurements of these decay rates should be the only acceptable experimental evidence, especially because measurements which are calibrated against other radioisotope systems are already biased by the currently accepted methodology that the secular community uses in their rock dating methods. Indeed, the 87Rb, 176Lu, and 187Re decay half-lives have all ultimately been calibrated against the U-Pb radioisotope system, yet there are now known measured variations in the 238U/235U ratio that is critical to that method (Brennecka and Wadhwa 2012; Hiess et al. 2012).
Therefore, the aim of this contribution is to further document the methodology behind and history of determining the present decay constants and half-lives of the parent radioisotopes used as the basis for the long-age dating methods. It is necessary to explore just how accurate these determinations are, whether there really is consensus on standard values for the half-lives and decay constants, and just how independent and objective the standard values are from one another between the different methods. Of course, it is to be expected that every long-lived radioactive isotope is likely to show similar variation and uncertainty in half-life measurements because these are difficult measurements to make. However, even small variations and uncertainties in the half-life values result in large variations and uncertainties in the calculated ages for rocks, and the question remains as to whether the half-life values for each long-lived parent radioisotope are independently determined. We continue here with samarium-147 (147Sm), which is the basis for the Sm-Nd dating method.
Samarium and Samarium-147 Decay
Samarium (Sm) and neodymium (Nd) are both rare-earth elements (REEs) with atomic numbers (Z) of 62 and 60 respectively. The rare-earth elements generally form ions with a 3+ charge whose radii decrease with increasing atomic number from 1.15 Å in lanthanum (La), atomic number 57, to 0.93 Å in lutetium (Lu), atomic number 71 (Faure and Mensing 2005). The REEs occur in high concentrations in several economically important minerals such as bastnaesite (CeFCO3), monazite (CePO4), and cerite [(Ca,Mg)2(Ce)8(SiO4)7・3H2O]. Furthermore, they occur as trace elements in common rock-forming minerals (silicates, phosphates, and carbonates) in which they replace major element ions. They may also reside in inclusions of certain accessory minerals in the common rock-forming silicates.
Minerals exercise a considerable degree of selectivity in admitting REEs into their crystal structures (Faure and Mensing 2005). Feldspar, biotite, and apatite tend to concentrate the light REEs (the Ce group), whereas pyroxenes, amphiboles, and garnet concentrate the heavy REEs (the Gd group). The selectivity of the rock-forming minerals for the light or heavy REEs obviously affects the REE concentrations of the rocks in which those minerals occur. Sm and Nd both belong to the light REEs, so they tend to concentrate in feldspar, biotite, and apatite. Thus the Sm and Nd concentrations in calc-alkaline plutonic and volcanic igneous rocks range from <1 ppm in ultramafic rocks to about 8 ppm Sm and 45 ppm Nd in granite. Alkali-rich igneous rocks have consistently higher Sm and Nd concentrations than the calc-alkaline suite, ranging up to about 15 ppm Sm and 85 ppm Nd.
Sm and Nd exhibit an unusual geochemical behavior, which arises from what is known as the “lanthanide contraction” (Faure and Mensing 2005). This contraction results from the way electrons fill their f shell orbitals. As a consequence, the ionic radius of Sm (Z = 62) is smaller than that of Nd (Z = 60). Even though the difference in the radii is small (Nd3+ = 1.08 Å; Sm3+ = 1.04 Å), Nd is preferentially concentrated in the liquid phase during partial melting of silicate minerals, whereas Sm remains in the residual solids. For this reason, basalt magmas have lower Sm/Nd ratios than the source rocks from which they formed. Thus this preferential partitioning of Nd into the melt phase has caused the rocks of the continental crust to be enriched in Nd relative to Sm compared to the residual rocks in the lithospheric mantle.
Even though the concentrations of Sm and Nd reach high values in accessory phosphate minerals such as apatite and monazite and in carbonatites, these minerals and carbonatites are still more enriched in Nd than in Sm and hence their Sm/Nd ratios are less than 0.32. Among the rock-forming silicate minerals, garnet is the only one with a high Sm/Nd ratio (0.54) even though its concentrations of Sm and Nd are both low (1–2 ppm). Several other rock-forming silicate minerals, such as K-feldspar, biotite, amphibole, and clinopyroxene, have higher Sm and Nd concentrations than garnet, but their Sm/Nd ratios are less than 0.32 in most cases.
Sm and Nd each have seven naturally-occurring isotopes. Of these 147Sm, 148Sm, and 149Sm are all radioactive, but the latter two have such long half-lives (about 1016 years) that they are not capable of producing measurable variations in the daughter isotopes 144Nd and 145Nd, even over supposed conventional cosmological intervals (1010 years) (Dickin 2005). Yet 147Sm only has an abundance of 15.0% in naturally occurring Sm (Lide and Frederikse 1995). Although the half-life of 147Sm is also very long (currently determined as 106 billion years), it decays by α-particle emission to 143Nd, a stable isotope of Nd. The relevant decay scheme is often depicted as:
147Sm → 143Nd + 4He + E
where 4He is an α-particle and E is the total decay energy. The energy of the 147Sm emitted α-particles is 2.23 MeV. This decay scheme has proven useful to uniformitarians for apparently dating terrestrial rocks, stony meteorites (both chondrites and achondrites), and lunar rocks.
There are two parameters by which the decay rate is measured and expressed, namely, the decay constant (λ) and the half-life (t½). The decay constant can be defined as the probability per unit time of a particular nucleus decaying, though strictly speaking probabilities do not have units associated with them and the decay constant is derived from a definitive functional relationship. In contrast, the half-life is the time it takes for half of a given number of the parent radionuclide atoms to decay. The two quantities can be almost used interchangeably, because they are related by the equation:-
t½ = ln 2/λ = 0.693/λ
The decay rate of 147Sm has not been all that difficult to determine once the necessary instrumentation was developed to accurately count the emitted α-particles. However, the Sm-Nd dating method has had its problems.
The lanthanide contraction causes the distribution of Sm and Nd to be opposite to that of Rb and Sr (Faure and Mensing 2005). And because Sm and Nd have very similar chemical properties (unlike Rb and Sr), large ranges of Sm/Nd ratios in whole-rock systems are rare, and in particular low Sm/Nd ratios near the vertical y-axis on an isochron dating graph are very rare. Therefore, because of the difficulty of obtaining a wide range of Sm/Nd ratios from a single rock body, and because of the greater technical demands of Nd isotope analysis, the Sm-Nd isochron dating method has been generally only applied to dating rock units for which Rb-Sr isochron dating has proven unsatisfactory. Many of those applications were also made before the U-Pb zircon dating method had reached its present level of development. Therefore, some of those rock units have subsequently been dated to apparent greater accuracy and precision by the U-Pb method. Nevertheless, the Sm-Nd method has continued to be used to date rocks and meteorites and thus the determination of the 147Sm half-life used by the method requires examination.
Determination Methods
Attempts to measure the α-radioactivity of Sm date back to the early 1930s. Famous names, such as Hevesy and Pahl, Curie and Joliot, Libby, and many more, are among the researchers who studied this phenomenon by various techniques (Begemann et al. 2001). At that time, before 147Sm had finally been identified as the isotope accountable for the α-radioactivity of Sm (Weaver 1950), the half-life was calculated in terms of the total element of Sm, with results ranging from 0.63 to 1.4 × 1012 years (that is, 630 to 1400 Byr). Even in 1949, when 148Sm (Wilkins and Dempster 1938) and 152Sm (Dempster 1948) had been reported erroneously to be responsible for the α-activity of samarium, Picciotto still published his result in terms of total Sm as 6.7 ± 0.4 × 1011 years (670 Byr), this quoted statistical error amounting to approximately 300 observed decays of 147Sm. Almost all attempts to measure the α-radioactivity of 147Sm have been by direct counting of α-particles, although two geological comparisons of radioisotope ages of individual meteorites have been used to confirm the direct counting measurements of the 147Sm half-life.
Direct counting
Initially direct measurements were done by counting α-particles registered on a photographic emulsion. For example, Picciotto (1949) used solutions of samarium sulfate to deposit layers of calculated weights of samarium across photographic emulsions which were then left exposed to the samarium α-activity for four to more than 19 days. At the end of each exposure time interval the tracks left by the α-particles on the emulsions when developed were counted. The calculated numbers of α-particles per second per gram of Sm were averaged to derive a decay rate in terms of the total Sm (all isotopes) of 6.7 ± 0.4 × 1011 years (670 Byr). Even though Beard and Wiedenbeck (1954) obtained a 147Sm half-life value using an ionization chamber (Geiger counter), they corroborated their result by checking the energy spectrum of their samarium source by exposing it for three weeks to a nuclear plate, which registered the tracks left by the α-particles. The mean track length compared favorably with previous emulsion experiments, and the energy distribution confirmed the tracks were produced by α-particles emitted by 147Sm.
A more recent use of the emulsion method by Martins, Terranova, and Moreira Correa (1992) involved spreading a calibrated solution of samarium nitrate over a glass plate which was then heated to leave a stable film of samarium oxide whose uniform thickness was measured. This method enabled accurate control, within the limits of volumetric error, of the quantity of samarium deposited on the glass plate. This glass plate was then contacted against a plastic emulsion plate for registration of the spontaneous 147Sm α-particle emission. After exposure for 30 days, stored in an underground laboratory to protect it from cosmic radiation, the emulsion was processed to etch the tracks left by the α-particles, which were then counted. The samarium oxide film was also checked by γ-spectrometry to rule out any contribution to the counted tracks from the possible presence of any U or Th atoms. A measurement of the 147Sm half-life was then calculated from the number of α-particle tracks produced from the known quantity of samarium in the exposure time period of 30 days. Though they did not account for possible α-particle energy loss in the samarium or the glass and plastic plates, this possibility was deemed negligible.
However, since the mid-1950s a variety of instruments have primarily been used for direct counting of 147Sm α-particles. In these instruments, the alpha (α) activity of 147Sm in a source material is counted over a designated time period, and divided by the total number of radioactive 147Sm atoms in the known quantity of Sm, based on Avogadro’s number and the isotopic abundance of 147Sm. Two types of such instruments have been used to count the α-particles emitted from different 147Sm sources—liquid scintillation spectrometers (Beard and Kelly 1958; Donhoffer 1964; Kinoshita, Yokoyama, and Nakanashi 2003; Kossert et al. 2009; Wright, Steinberg, and Glendenin 1961), and ionization chambers or Geiger counters (Beard and Wiedenbeck 1954; Gupta and MacFarlane 1970; Karras and Nurmia 1960; Kinoshita, Yokoyama, and Nakanashi 2003; MacFarlane and Kohman 1961). A variety of 147Sm sources have also been used, namely, samarium octoate (Wright, Steinberg, and Glendenin 1961), samarium oxide (Beard and Wiedenbeck 1954; Kinoshita, Yokoyama, and Nakanashi 2003; Kossert et al. 2009; MacFarlane and Kohman 1961; Su et al. 2010), and samarium metal (Gupta and MacFarlane1970; Su et al. 2010).
In the most recent half-life determination, Su et al. (2010) deposited 147Sm-enriched metal and oxide on pure quartz glass substrates by vacuum evaporation and sputtering respectively, and then checked the uniformity of the thicknesses of these samples by exposing them to plastic emulsion plates in direct contact with them. However, in using this method it is difficult to compensate for α-energy loss due to absorption. After 100 hours exposure the emulsion plates were chemically etched and the α-particle tracks were observed and counted. This does not appear to be a good way of establishing uniformity of thickness, whereas α-gauging would be a better method. Nevertheless, the α-activities of the two samples were then measured by silicon surface-barrier detectors placed in vacuum chambers for a period of 200 hours (8 days 8 hours). Finally the 147Sm half-life was then calculated from the α-activity spectra for each sample (Sm metal and Sm oxide).
A liquid scintillation counter or spectrometer detects and measures ionizing radiation by using the excitation effect of incident α-particles on a scintillator material, and detecting the resultant light pulses. It consists of a scintillator which generates photons of light in response to incident α-particles, a sensitive photomultiplier tube which converts the light to an electrical signal, and electronics to process this signal.
Liquid scintillation counting measures the α-activity of a sample, prepared by mixing the α-active material with a liquid scintillator, and counting the resultant photon emissions. This allows for more efficient counting due to the intimate contact of the α-activity with the scintillator. Samples are dissolved or suspended in a “cocktail” containing a solvent, typically some form of a surfactant, and small amounts of other additives known as “fluors” or scintillators.
The radioactive sample is then placed in a vial containing a premeasured amount of scintillator cocktail and this vial plus vials containing known amounts of 147Sm are loaded into the liquid scintillation counter. Many counters have two photomultiplier tubes connected in a coincidence circuit. The coincidence circuit assures that genuine light pulses, which reach both photomultiplier tubes, are counted, while spurious pulses (due to line noise, for example), which would only affect one of the tubes, are ignored.
When a charged particle strikes the scintillator, its atoms are excited and photons are emitted. These are directed at the photomultiplier tube’s photocathode, which emits electrons by the photoelectric effect. These electrons are electrostatically accelerated and focused by an electrical potential so that they strike the first dynode of the tube. The impact of a single electron on the dynode releases a number of secondary electrons which are in turn accelerated to strike the second dynode. Each subsequent dynode impact releases further electrons, and so there is a current amplifying effect at each dynode stage. Each stage is at a higher potential than the previous stage to provide the accelerating field. The resultant output signal at the anode is in the form of a measurable pulse for each photon detected at the photocathode, and is passed to the processing electronics. The pulse carries information about the energy of the original incident α-radiation on the scintillator. Thus both the intensity and energy of the α-particles can be measured.
The scintillation spectrometer consists of a suitable scintillator crystal, a photomultiplier tube, and a circuit for measuring the height of the pulses produced by the photomultiplier. The pulses are counted and sorted by their height, producing an x–y plot of scintillator flash brightness versus number of flashes, which approximates the energy spectrum of the incident α-radiation.
The ionization chamber is the simplest of all gas-filled radiation detectors, and is widely used for the detection and measurement of certain types of ionizing radiation, including α-particles (fig. 1). Conventionally, the term “ionization chamber” is used exclusively to describe those detectors which collect all the charges created by direct ionization within the gas through the application of an electric field. It only uses the discrete charges created by each interaction between the incident radiation and the gas, and does not involve the gas multiplication mechanisms used by other radiation instruments, such as the Geiger- Müller counter or the proportional counter.
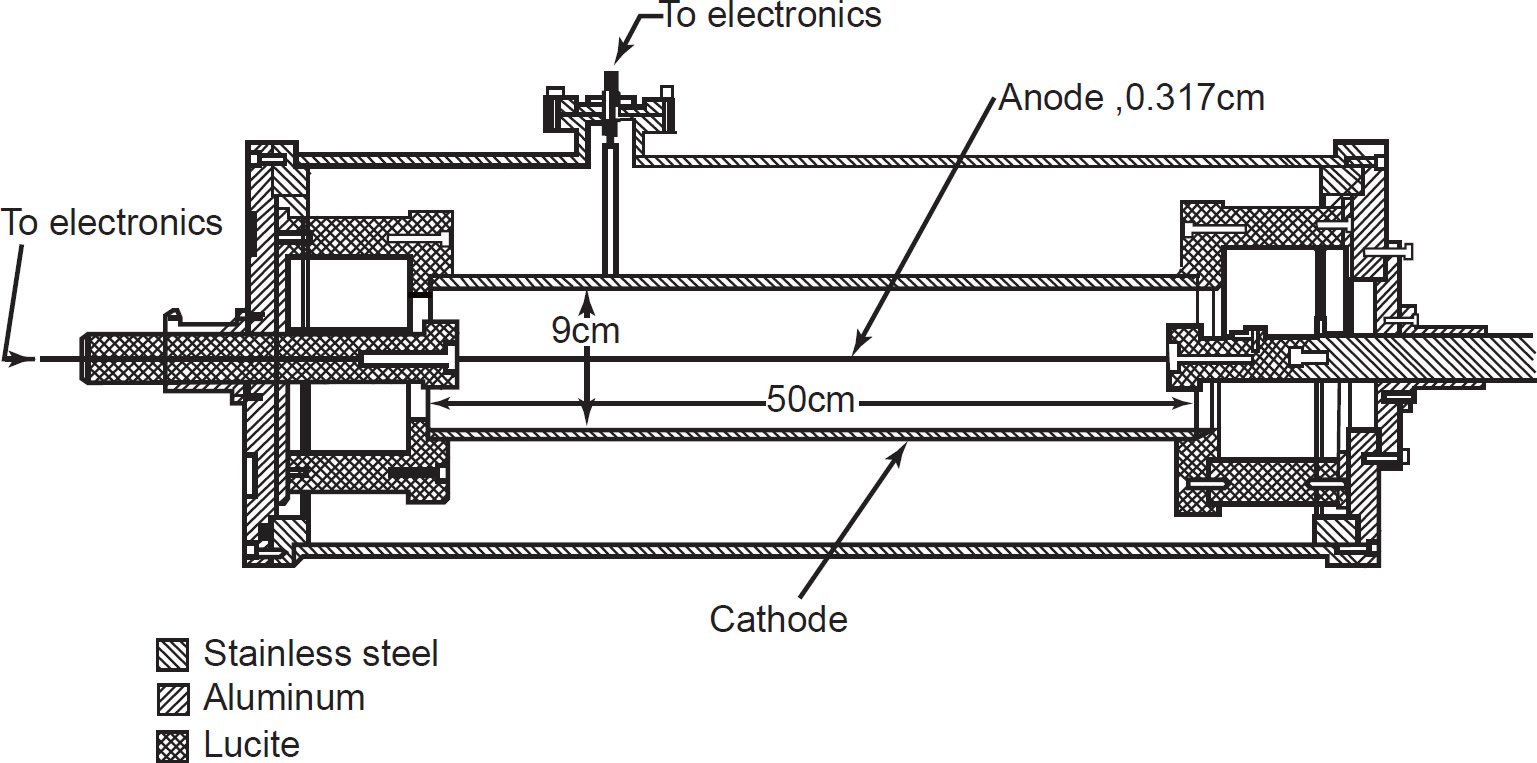
Fig. 1. Schematic diagram of the cylindrical ionization chamber (alpha spectrometer) used by Gupta and MacFarlane (1970) in their determination of the 147Sm half-life.
An ionization chamber measures the current from the number of ion pairs created within a gas caused by incident α-radiation. It consists of a gas-filled chamber with two electrodes, known as the anode and cathode (fig. 1). The electrodes may be in the form of parallel plates, or a cylinder arrangement with a coaxially located internal anode wire. A voltage is applied between the electrodes to create an electric field in the fill gas. When gas between the electrodes is ionized by incident ionizing α-radiation (or β- or γ-radiation), ion-pairs are created and the resultant positive ions and dissociated electrons move to the electrodes of the opposite polarity under the influence of the electric field. This generates an ionization current which is measured by an electrometer. The electrometer must be capable of measuring the very small output current which is in the region of femtoamperes (10-15 amps) to picoamperes (10-12 amps), depending on the chamber design, α-radiation dose and applied voltage. The unique feature of ionization chambers is that the electric field strength is low enough that no multiplication of ion pairs occurs. Hence the current generated at a given voltage depends on the type and energy of the incident radiation but is independent over a range of applied voltages, approximately 100–300 volts.
Each ion pair creates deposits or removes a small electric charge to or from an electrode, such that the accumulated charge is proportional to the number of ion pairs created, and hence the α-radiation dose. This continual generation of charge produces an ionization current, which is a measure of the total ionizing dose entering the chamber. The electric field also enables the device to work continuously by mopping up electrons, which prevents the fill gas from becoming saturated, where no more ions could be collected, and by preventing the recombination of ion pairs, which would diminish the ion current. This mode of operation is referred to as “current” mode, meaning that the output signal is a continuous current, and not a pulse output as in the cases of the Geiger-Müller tube or the proportional counter. In the ionization chamber operating region the collection of ion pairs is effectively constant over a range of applied voltage, as due to its relatively low electric field strength the ion chamber does not have any multiplication effect. This is in distinction to the Geiger-Müller tube or the proportional counter whereby secondary electrons, and ultimately multiple avalanches, greatly amplify the original ion-current charge. In the proportional counter the electric field produces discrete, controlled avalanches such that the energy and type of radiation can be determined at a given applied field strength.
The Geiger–Müller counter, also called a Geiger counter, is also used for measuring ionizing radiation. It detects radiation such as α-particles, using the ionization produced in a Geiger–Müller tube. The processing electronics displays the result. The Geiger-Müller tube is filled with an inert gas such as helium, neon, or argon at low pressure, to which a high voltage is applied. The tube briefly conducts an electrical charge when a particle or photon of incident α-radiation makes the gas conductive by ionization. The ionization is considerably amplified within the tube by an avalanche effect to produce an easily measured detection pulse, which is fed to the processing and display electronics. The electronics also generates the high voltage, typically 1000–1400 volts, which has to be applied to the Geiger-Müller tube to enable its operation. The voltage must be high enough to produce avalanche effects for all incident radiation. Thus a Geiger-Müller tube has no ability to discriminate between incident radiations; all radiation produces the same current.
There are two main limitations of the Geiger counter. Because the output pulse from a Geiger- Müller tube is always the same magnitude regardless of the energy of the incident α-radiation, the tube cannot differentiate between radiation types. A further limitation is the inability to measure high α-radiation intensities due to the “dead time” of the tube. This is an insensitive period after each ionization of the gas during which any further incident α-radiation will not result in a count, and the indicated rate is therefore lower than actual. Typically the dead time will reduce indicated count rates above about 104 to 105 counts per second depending on the characteristic of the tube being used. Whilst some counters have circuitry which can compensate for this, for accurate measurements ion chamber instruments are preferred to measure high radiation rates.
Counting efficiencies of liquid scintillation counters under ideal conditions range from about 30% for tritium (a low-energy β-emitter), to nearly 100% for phosphorus-32 (32P), a high-energy β-emitter. Thus counting efficiencies for α-particles are within this range, which is <100%. Some chemical compounds (notably chlorine compounds) and highly colored samples can interfere with the counting process. This interference, known as quenching, can be overcome through data correction or through careful sample preparation. In ionization counters the counting efficiency is the ratio between the number of α-particles or photons counted and the number of α-particles or photons of the same type and energy emitted by the α-radiation source. Counting efficiencies vary for different isotopes and sample compositions, and for different scintillation counters. Poor counting efficiency can be caused by an extremely low energy to light conversion rate (the scintillation efficiency), which, even optimally, will be a small value. It has been calculated that only some 4% of the energy from a β-emission event is converted to light by even the most efficient scintillation cocktails. Proportional counters and end-window Geiger-Müller tubes have a very high efficiency for all ionizing particles that reach the fill gas. Nearly every initial ionizing event in the gas will result in avalanches, and thereby an output signal. However the overall detector efficiency is largely affected by attenuation due to the window or tube body through which particles have to pass. They are also extremely sensitive to various types of background radiation due to their lack of discrimination.
Judged from the fact that many of these direct counting experiments, particularly the earlier ones, have yielded results that are not compatible with one another within the stated uncertainties (see below), it would appear that not all the measurement uncertainties are accounted for, and therefore the stated uncertainties are likely unrealistically small and typically are underestimated. Begemann et al. (2001) maintain that many of such experiments are likely plagued by unrecognized systematic errors. As the nature of these errors is obscure, it is not straightforward to decide which of the, often mutually exclusive, results of such direct counting experiments is closest to the true value, although most of the post-early-1960s experiments appear to converge on a common value (see below). Furthermore, the presence of unknown systematic biases makes any averaging dangerous. It is possible that reliable results of careful workers, listing realistic uncertainties, will not be given the weights they deserve—this aside from the question of whether it makes sense to average numbers that by far do not all agree within the stated uncertainties.
Geological comparisons of methods
A second approach used by secular scientists to determine the 147Sm decay half-life has been to date geological samples whose ages have also been measured by other methods with presumably more reliable decay constants (Dickin 2005; Faure and Mensing 2005). This essentially involves circular reasoning, because it is being assumed the other radioisotope dating methods, principally the U-Pb method, gives the reliable dates to which the 147Sm half-life can be calibrated to bring the Sm-Nd radioisotope ages into agreement. It should be noted, however, that this is hardly objective, because all the radioisotope ages of rocks could be wrong due to the underlying unprovable and suspect assumptions on which all the radioisotope dating methods are based. Nevertheless, a few geological determinations of the 147Sm half-life were made in the 1970s using components of individual achondrite meteorites (Dickin 2005, 70–71; Lugmair 1974; Lugmair, Scheinin, and Marti 1975; Lugmair and Marti 1977).
This method has the disadvantage that it involves geological uncertainties, such as whether all isotopic systems closed at the same time and remained closed. However, it is claimed to still provide a useful check on the laboratory determinations by direct physical counting. Nevertheless, this approach entails multi-chronometric dating of minerals and components in individual meteorites and cross-calibration of different radioisotopic age systems by adjusting the decay constant of the Sm-Nd system so as to force agreement with the age obtained via another dating system, usually U-Pb (Begemann et al. 2001). In essence, because the half-life of 238U is claimed to be the most accurately known of all relevant radionuclides, this usually amounts to expressing ages in units of the half-life of 238U.
Results of the Samarium-147 Decay Determinations
During the last 80 years numerous determinations of the 147Sm decay constant and half-life have been made using these methods. The results are listed with details in Table 1. The year of the determination versus the value of the half-life is plotted in Fig. 2. In each case the data points plotted have been color-coded the same to differentiate the values as determined by the two approaches that have been used—direct counting, and geological comparisons with other radioisotope dating methods.
Table 1. Determinations of the 147Sm decay rate expressed in terms of the half-life using direct physical counting experiments, and comparisons of radioisotope ages of terrestrial minerals and rocks, and meteorites.
Determination of the Sm Decay Rate |
||||||
| Date | Half-Life (Byr) | Uncertainty (Byr) | Method | Instrument | Notes | Source |
|---|---|---|---|---|---|---|
| 1936 | 150 | ± 11 | direct counting | emulsion plate | Hosemann 1936 | |
| 1949 | 100 | ± 6 | direct counting | emulsion plate | Picciotto 1949 | |
| 1954 | 125 | ± 6 | direct counting | ionization chamber | 4 π Geiger counter | Beard and Wiedenbeck 1954 |
| 1958 | 128 | ± 4 | direct counting | liquid scintillation | Beard and Kelly 1958 | |
| 1960 | 114 | ± 5 | direct counting | ionization chamber | Karras and Nurmia 1960 | |
| 1960 | 117 | ± 5 | direct counting | ionization chamber | Karras 1960 | |
| 1961 | 113 | direct counting | Graeffe and Nurmia 1961 | |||
| 1961 | 115 | ± 5 | direct counting | ionization chamber | MacFarlane and Kohman 1961 | |
| 1961 | 105 | ± 1 | direct counting | liquid scintillation | Wright, Steinberg, and Glendenin 1961 | |
| 1964 | 104 | ± 3 | direct counting | liquid scintillation | Donhoffer 1964 | |
| 1965 | 108 | ± 2 | direct counting | liquid scintillation | Valli et al. 1965 | |
| 1970 | 106 | ± 2 | direct counting | ionization chamber | Gupta and MacFarlane 1970 | |
| 1975 | 106 | geological comparisons | Juvinas basaltic achondrite meteorite | Lugmair, Sheinin, and Marti 1975 | ||
| 1977 | 106 | geological comparisons | Angra dos Reis achondrite meteorite | Lugmair and Marti 1977 | ||
| 1978 | 106 | ± 0.8 | direct counting | weighted average of four measures | Lugmair and Marti 1978 | |
| 1987 | 105 | ± 4 | direct counting | Al-Bataina and Jänecke 1987 | ||
| 1992 | 123 | ± 4 | direct counting | emulsion plate | Martins, Terranova, and Moreira Correa 1992 | |
| 2001 | 106 | ± 4 | direct counting | emulsion plate | correction of Martins et al. 1992 | Begemann et al. 2001 |
| 2003 | 117 | ± 2 | direct counting | alpha spectrometer | with vacuum chamber (also liquid scintillation) | Kinoshita, Yokoyama, and Nakanashi 2003 |
| 2009 | 107 | ± 0.9 | direct counting | liquid scintillation | Kossert et al. 2009 | |
| 2010 | 106 | ± 1 | direct counting | alpha spectrometer | with vacuum chamber, Sm metal | Su et al. 2010 |
| 2010 | 107 | ± 1 | direct counting | alpha spectrometer | with vacuum chamber, Sm oxide | Su et al. 2010 |
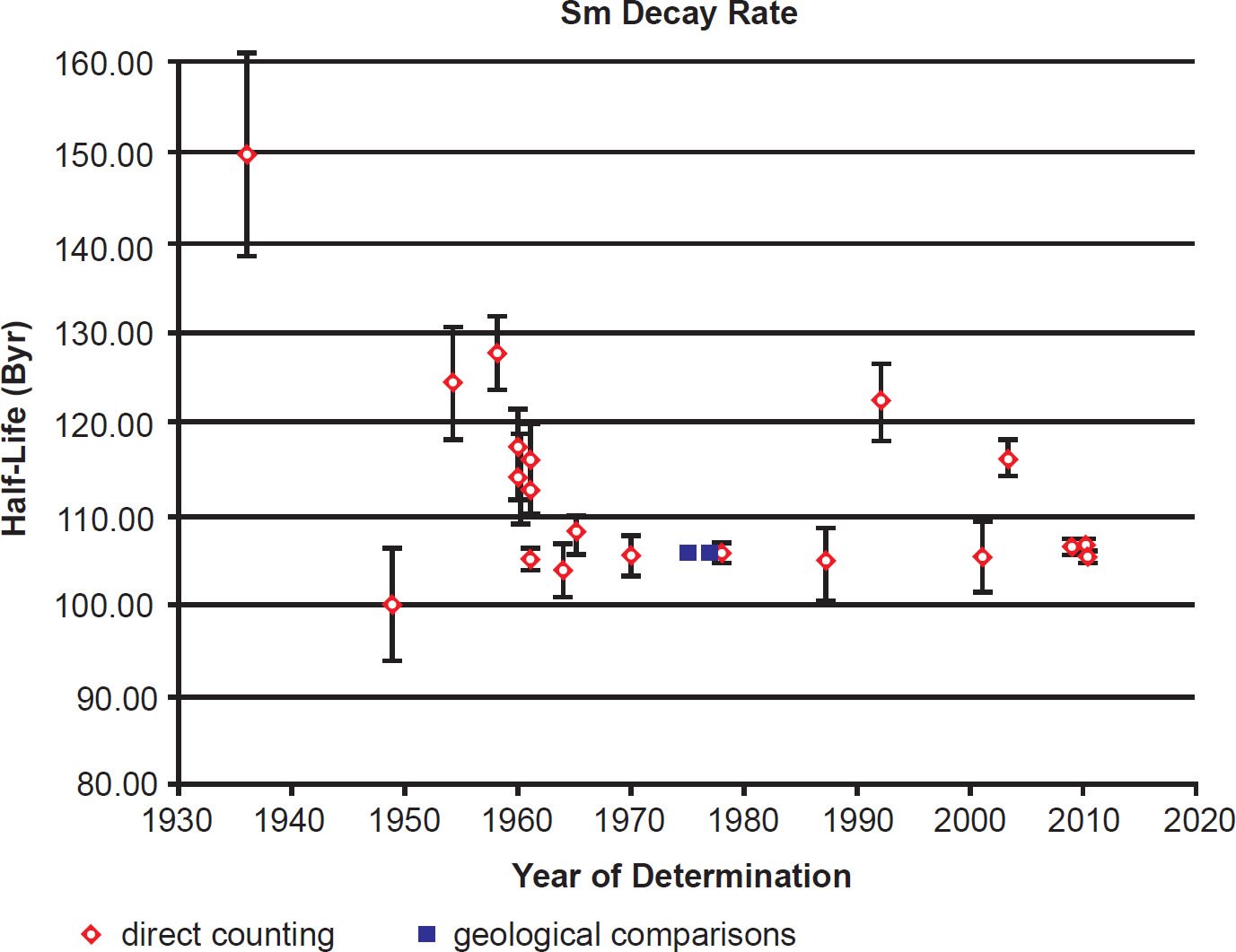
Fig. 2. Plot of each 147Sm half-life determination versus the year of its determination, color-coded according to the method of its determination. The error bars for each determination are also plotted from the error values listed in Table 1.
Discussion
Results obtained after 1954, and particularly during the 1960s and the ensuing decade, began to converge towards a 147Sm common half-life value (see table 1 and fig. 2). In the early 1970s, when Lugmair and his colleagues began to develop the decay of 147Sm to 143Nd as a dating tool (Lugmair 1974), they used only a weighted average of the last four half-life measurements at that time, those of Wright, Steinberg, and Glendenin (1961), Donhoffer (1964), Valli et al. (1965), and Gupta and MacFarlane (1970) (Lugmair and Marti 1978). They range from 1.04 to 1.08 × 1011 years (104 to 108 Byr) with a weighted mean of 1.060 ± 0.008 × 1011 years (106 ± 0.8 Byr) (1σ uncertainty). It is worth noting that the statistical error of this weighted mean infers that more than 10,000 α-decays of 147Sm have occurred to produce this result. Nevertheless, it should be noted that three of those measurements were made using liquid scintillation counters and one using an ionization chamber (see table 1), all of which have different counting efficiencies, as already discussed. Nevertheless, that 147Sm half-life value has been adopted by all geochronologists and cosmochronologists since that time (the late 1970s).
There have been five more modern measurements of the 147Sm half-life since the 1970s (table 1). The first by Al-Bataina and Jänecke (1987) with a value of 1.05 ± 0.04 × 1011 years (105 ± 4 Byr) agrees very well with the previous direct counting results of Donhoffer (1964), Gupta and MacFarlane (1970), Valli et al. (1965), and Wright, Steinberg, and Glendenin (1961), as well as with the geological comparisons with Pb-Pb ages of meteorites by Lugmair (1974), Lugmair, Scheinin, and Marti (1975), and Lugmair and Marti (1977) (table 1). It is also in close agreement with subsequent determinations by Kossert et al. (2009) and Su et al. (2010) (table 1). However, the determination by Martins, Terranova, and Moreira Correa (1992) of 1.23 ± 0.04 × 1011 years (123 ± 4 Byr) is substantially higher than the Al-Bataina and Jänecke (1987) determination of 1.05 ± 0.04 × 1011 years (105 ± 4 Byr), as is the Kinoshita, Yokoyama, and Nakanashi (2003) determination of 1.17 ± 0.02 × 1011 years (117 ± 2 Byr) (table 1). These variant results can be easily seen in Fig. 2.
Begemann et al. (2001) claimed that because there is good agreement of ages obtained using the generally accepted 147Sm half-life value of 1.06 ± 0.01 × 1011 years (106 ± 1 Byr) with ages obtained by the U-Pb (Pb-Pb) systems (for example, Lugmair 1974; Lugmair and Marti 1977; Lugmair, Scheinin, and Marti 1975), and because the 238U and 235U half-lives are more accurately known, the determination by Martins, Terranova, and Moreira Correa (1992) of 1.23 ± 0.04 × 1011 years (123 ± 4 Byr) should be viewed with caution, and indeed, that discrepant result most likely is an artifact. Begemann et al. (2001) noted that Martins, Terranova, and Moreira Correa (1992) reported in their experimental procedure the number of α-decays was registered on a “thin film of natural samarium oxide Sm2O3 with an overall uniform thickness of (0.207 ± 0.005) mg/cm2.” However, in their subsequent calculation of the decay constant, Martins, Terranova, and Moreira Correa (1992) apparently used the same thickness as for pure samarium element instead of correcting for oxygen. If this was a mistake as Begemann et al. (2001) claimed, then the published half-life value should have been multiplied by the weight ratio Sm2/Sm2O3 = 0.8624, provided the Sm2O3 used was truly stoichiometric. This would have yielded a 147Sm half-life value of 1.06 × 1011 years (106 Byr), which is in very good agreement with the previous five direct counting measurements (table 1). Begemann et al. (2001) reported that according to a private communication with one of the authors of the Martins, Terranova, and Moreira Correa (1992) paper, it is very likely that this explanation is correct, although it is not possible to give a definitive answer. For this and other reasons, Begemann et al. (2001) stated that they do not share the authors’ opinion that their result “may be considered as the most accurate measurement of the half-life performed up to now” (that is, up to 1992). Nevertheless, Su et al. (2010) performed parallel determinations using Sm metal and Sm2O3 (as described above) and obtained similar results of 1.06 ± 0.01 × 1011 years (106 ± 1 Byr) and 1.07 ± 0.01 × 1011 years (107 ± 1 Byr) respectively (table 1).
What then can be said about the Kinoshita, Yokoyama, and Nakanashi (2003) determination of 1.17 ± 0.02 × 1011 years (117 ± 2 Byr) (table 1)? Actually, it can be argued that their careful experimental approach using multiple repeated measurements with multiple 147Sm sources using both an alpha spectrometer and a liquid scintillation spectrometer to measure the number of emitted α-particles per unit time, plus their detailed analysis of the counting efficiencies of the instrumental techniques they used, makes their determinations of the 147Sm half-life more robust than any other determinations. Kossert et al. (2009) subsequently questioned the Kinoshita, Yokoyama, and Nakanashi (2003) determined 147Sm half-life value because it did not agree with many other determined values. They also incorrectly asserted that Kinoshita, Yokoyama, and Nakanashi (2003) did not measure the isotopic ratio when their paper clearly reports that they did. These are not valid reasons to dismiss their determined 147Sm half-life value. Worse still, rather than engage in discussion, Su et al. (2010) simply ignored the Kinoshita, Yokoyama, and Nakanashi (2003) determined 147Sm half-life value. Yet the reality is that the Kinoshita, Yokoyama, and Nakanashi (2003) determined 147Sm half-life value of 117 ± 2 Byr is in very good agreement with the four direct counting values of 114 ± 5 Byr of Karras and Nurmia (1960), 117 ± 5 Byr of Karras (1960), and 115 ± 5 Byr of Gupta and MacFarlane (1970) who all used ionization chambers for their determinations, and of 113 Byr of Graeffe and Nurmia (1961). However, it seems that the accepted 147Sm half-life value of 106 Byr is determined by “majority vote” because it is supported by the seven direct counting determinations of Al-Bataina and Jänecke (1987), Donhoffer (1964), Gupta and MacFarlane (1970), Kossert et al. (2009), Su et al. (2010), Valli et al. (1965), and Wright, Steinberg, and Glendenin (1961) (table 1).
Kinoshita, Yokoyama, and Nakanashi (2003) were well aware that the 147Sm half-life values reported from 1954 to 1970 showed some scatter between 104 Byr and 128 Byr, so they purposed to design their experimental procedures to thoroughly reevaluate the 147Sm half-life by means of a developed alpha spectrometer with counting sources prepared in a manner different from those adopted in those earlier determination experiments. Two kinds of commercially available Sm2O3 reagents of 99.9% purity and two kinds of commercially available Sm standard solutions for atomic absorption spectroscopy were prepared as four standard Sm solutions (with known concentrations in μg-Sm/g-solution). These were labelled as Sm-A, Sm-B, Sm-C, and Sm-D. Radioactive and non-radioactive impurities in these Sm solutions were measured by low-level gamma spectrometry, neutron activation, ICP-MS spectrometry, and thermal ionization mass spectrometry (TIMS), and it was confirmed that the solutions did not contain any detectable impurities, and that the isotopic composition was natural (that is, 15.0% 147Sm).
Kinoshita, Yokoyama, and Nakanashi (2003) used calibrated solutions of the α-radioactive nuclides 210Po, 238U, and 241Am as internal standards in preparation of the counting sources for alpha spectrometry. Known aliquots of each of the four Sm standard solutions were mixed well with known amounts of the calibrated 210Po, 238U, and 241Am standard solutions to produce ten kinds of combinations. Each mixture was then evaporated on watch glasses and the amount of Sm on each watch glass was adjusted to ~100 μg, which means that there was approximately 15 μg of 147Sm on each watch glass. Alpha spectrometry, using a silicon surface-barrier detector with an active area of 450 mm2, was carried out for one to two weeks for each of the counting sources, and the α-disintegration rate of the known amounts of 147Sm was determined by reference to the α-activities of the internal standards.
Measurements of the α-disintegration rates of the known amounts of 147Sm were also carried out concurrently by Kinoshita, Yokoyama, and Nakanashi (2003) using a liquid scintillation spectrometer. However, only the 241Am internal standard solution was added to each of the four Sm standard solutions. Each mixture was prepared for the measurements and then 10 ml of either the Amersham ACS II scintillation cocktail or the p-terphenyl + POPOP + toluene scintillation cocktail was added. A blank sample for background liquid scintillation measurement was also prepared in the same way. The liquid scintillation counting was continued for five hours for each of the counting sources. The same cocktail mixture for establishing the quench curve was used in determining the counting efficiency.
Kinoshita, Yokoyama, and Nakanashi (2003) then calculated a series of 147Sm half-life values based on the 147Sm α-activity of each of the prepared counting sources calibrated against the α-activity of each internal standard measured by the alpha spectrometer, and these are plotted in Fig. 3, along with results from several earlier determinations. They also calculated a series of 147Sm half-life values measured with the liquid scintillation spectrometer, and these are plotted in Fig. 4. The attached error for each plotted half-life value included the nominal systematic errors in the calibration of the α-emitting standard and in the measurement of the isotopic abundance of 147Sm, in addition to the statistical error of 1σ in α-counting. It is quite obvious from Figs. 3 and 4 that the 147Sm half-life values obtained by Kinoshita, Yokoyama, and Nakanashi (2003) using an alpha spectrometer and a liquid scintillation spectrometer respectively agree very closely with each other within the error bars shown.
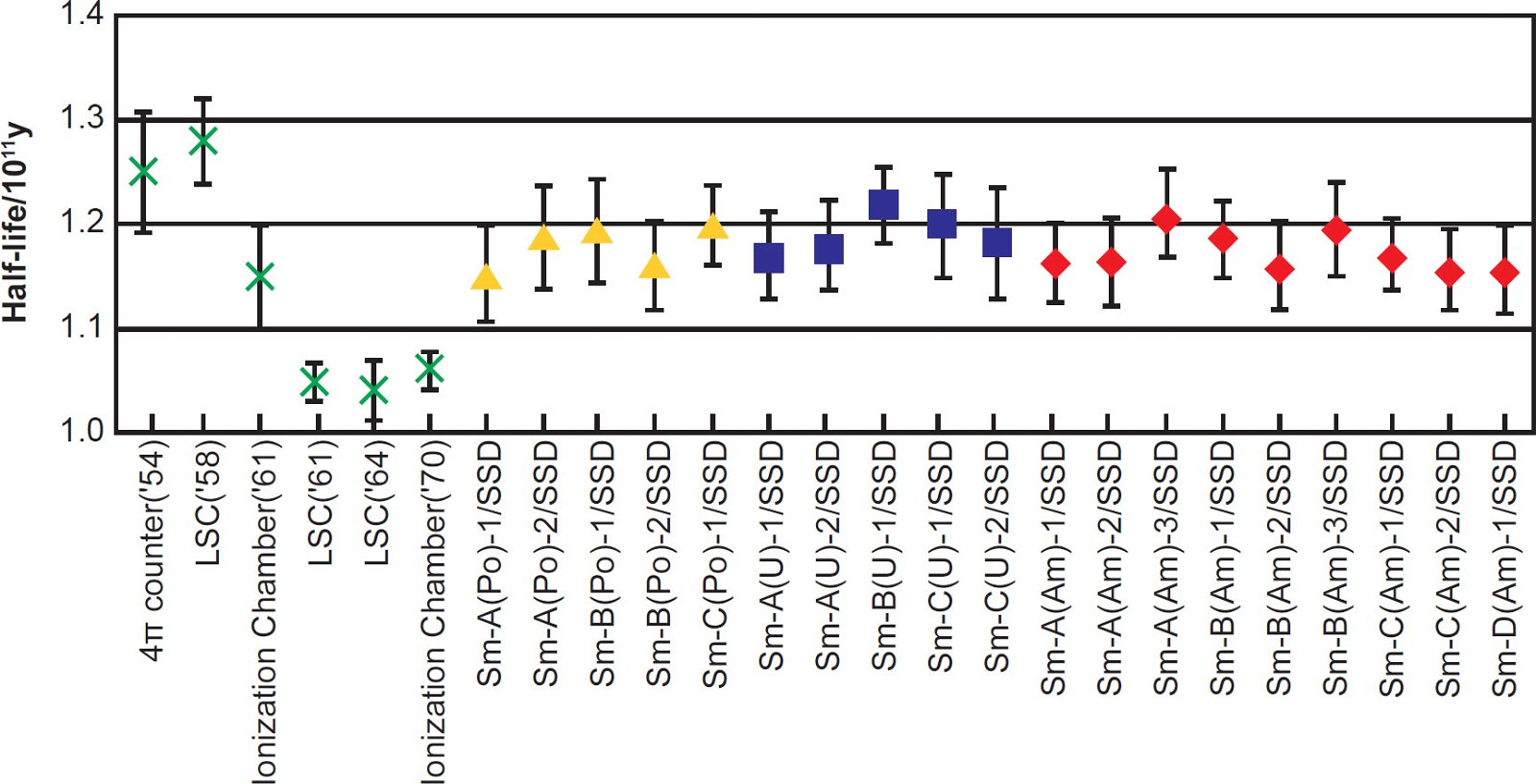
Fig. 3. The 147Sm half-life values and their errors determined by alpha spectrometer using a silicon surface-barrier detector (after Kinoshita, Yokoyama, and Nakanashi [2003]). The values from earlier determinations are indicated by cross symbols, and values obtained by Kinoshita, Yokoyama, and Nakanashi (2003) are indicated by closed symbols. The prepared sources are referred to as the sample names with the original solution name, the reference standard, source number, and the measurement method.
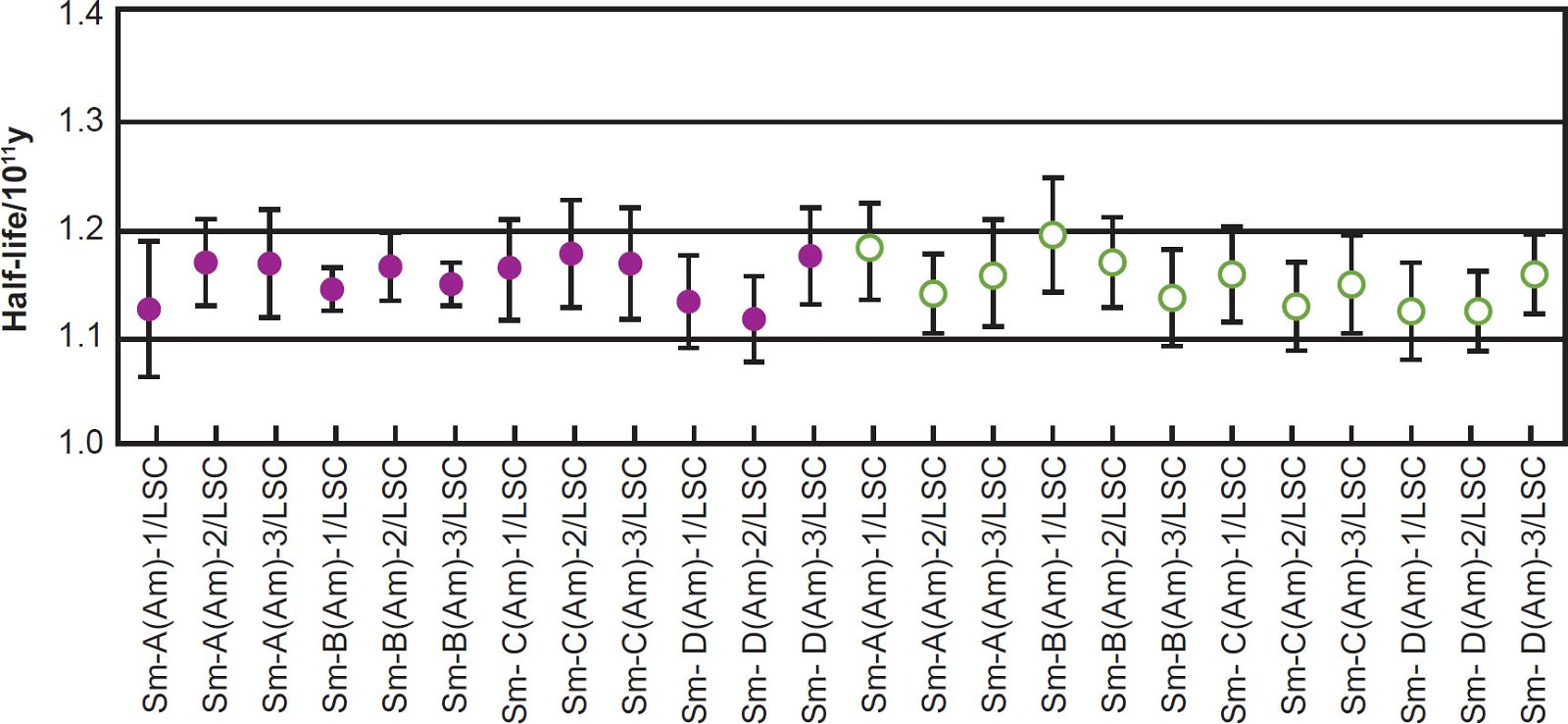
Fig. 4. The 147Sm half-life values and their errors determined by liquid scintillation spectrometer (after Kinoshita, Yokoyama, and Nakanashi [2003]). The prepared sources are depicted as in Fig. 2. The Amersham ACS II scintillation cocktail is shown as closed symbols, and the p-terphenyl + POPOP + toluene scintillation cocktail is denoted with open symbols.
Kinoshita, Yokoyama, and Nakanashi (2003) were also careful to discuss the sources of error and their potential adverse effects on their 147Sm half-life determination. They admitted that, in alpha spectrometry for a deposited counting source, self-absorption of α-particles in the source is a serious problem. However, the energy loss and absorption of α-particles in the window-layer of the silicon surface-barrier detector (~50 nm) and in the vacuum chamber (<4 Pa) are negligible. As to the extent of absorption in their alpha spectrometry measurements, they argued that since the thickness of the residue of Sm and the α-emitting standard on the watch glass was less than 15 μg/cm2, energy loss and absorption of α-particles from 147Sm and the α-emitting standard of the counting source was expected to be negligible. On the other hand, while the counting efficiency of the liquid scintillation spectrometer is usually high (~100%), the spectrometer has the disadvantages of high background and poor energy-resolution. Hence, they concluded that in spite of the agreement between the mean 147Sm half-life value of 115 ± 2 Byr measured with the liquid scintillation spectrometer and the mean 147Sm half-life value of 117 ± 2 Byr measured with the surface-barrier detector, within the error, the former value was regarded as supporting data for the latter value because of these described disadvantages.
Kinoshita, Yokoyama, and Nakanashi (2003) determined that the arithmetic mean of the 147Sm half-life values obtained in their experimental work for the 19 counting sources by alpha spectrometry (fig. 3) was 117 ± 2 Byr, the stated associated error being one standard deviation. This average 147Sm half-life value was thus about 10% longer than the then, and still, currently adopted value of 106 ± 2 Byr. However, Kinoshita, Yokoyama, and Nakanashi (2003) noted that in the earlier determinations the half-life of 147Sm was obtained by measuring the 147Sm α-activity with a 4π gas-flow counter (Beard and Wiedenbeck 1954), liquid scintillation spectrometers (Beard and Kelly 1958; Donhoffer 1964; Wright, Steinberg, and Glendenin 1961), and ionization chambers (Gupta and MacFarlane 1970; MacFarlane and Kohman 1961) from sources with the number of 147Sm atoms in them also measured. Because the 147Sm half-life is then calculated conventionally from the obtained values of the 147Sm α-activity and the number of 147Sm atoms, the experimental errors in measuring those two values result in inaccurate determinations of the 147Sm half-life. For example, impurities in the Sm reagent bring error into the number of 147Sm atoms in the counting source, and uncertainty in the counting efficiency, self-absorption of the counting source and radioactive impurities in the Sm reagent bring error into the value of the 147Sm α-activity. Kinoshita, Yokoyama, and Nakanashi (2003) thus suggested that the purity of the Sm reagent was not sufficient in the earlier experimental determinations. They also suspected that the corrections for counting efficiency and self-absorption were not appropriate in the earlier experimental determinations. High background and poor energy resolution of the liquid scintillation spectrometers used in the earlier experimental determinations might also have resulted in inaccurate 147Sm half-life values. Since Kinoshita, Yokoyama, and Nakanashi (2003) were confident that all these sources of error were excluded from their experimental work, in contrast to the earlier experimental determinations, they concluded that their result of 117 ± 2 Byr for the 147Sm half-life is reliable.
As already noted, Kossert et al. (2009) subsequently questioned the Kinoshita, Yokoyama, and Nakanashi (2003) result of 117 ± 2 Byr for the 147Sm half-life. They were confident that they had accurately determined the 147Sm half-life as being 107 ± 0.9 Byr because they had expended great effort to evaluate the liquid scintillation counting efficiency to be 100%, because the number of 147Sm atoms in the Sm reagent had been measured by means of ICP-OES (inductively coupled plasma optical emission spectrometry) using a reference standard from the National Institute of Standards and Technology, and because their result agreed well with most of the other measurement results and the recommended value. However, as has been already noted, a significant number of other measurement results also disagree with the recommended 147Sm half-life value of 106 ± 2 Byr and are closer to the Kinoshita, Yokoyama, and Nakanashi (2003) result of 117 ± 2 Byr. Furthermore, while Kossert et al. (2009) asserted that Kinoshita, Yokoyama, and Nakanashi (2003) measured quite low activities in their experiments, they incorrectly accused Kinoshita, Yokoyama, and Nakanashi (2003) of not measuring the Sm isotopic ratio when they clearly stated that they did. Such an error would cast doubt on the Kossert et al. (2009) assessment of the experimental work of Kinoshita, Yokoyama, and Nakanashi (2003), especially as Kossert et al. (2009) admitted they did not have enough information on the Kinoshita, Yokoyama, and Nakanashi (2003) measurement details, in particular on the treatment of the background and tailing of the α-peaks in their measured spectra. But Kinoshita, Yokoyama, and Nakanashi (2003) did provide measurement details, as already described, and the α-peaks in their spectra measured by alpha spectrometer are very narrow, sharp, and distinct with a short tail and very low background, as illustrated in their report. So the reality is that Kossert et al. (2009) questioned the Kinoshita, Yokoyama, and Nakanashi (2003) result primarily because it didn’t agree well with most of the other recent measurement results and the recommended value, even though Kinoshita, Yokoyama, and Nakanashi (2003) did 19 alpha spectrometer determinations using combinations of four standard Sm solutions and three internal standards (fig. 3) backed up by 24 liquid scintillation spectrometer determinations yielding essentially the same results (fig. 4).
On the other hand, Su et al. (2010) simply ignored the Kinoshita, Yokoyama, and Nakanashi (2003) determined 147Sm half-life value of 117 ± 2 Byr after an introductory passing reference to it, and simply asserted that the “absolute” half-life they had determined, 106 ± 1 Byr (Sm metal) and 107 ± 1 Byr (Sm2O3), is consistent with the recommended value of 106 Byr. Yet Su et al. (2010) used a silicon surface-barrier detector coupled to an alpha spectrometer to similarly obtain their 147Sm α-activity peaks, just as Kinoshita, Yokoyama, and Nakanashi (2003) had done. And Su et al. (2010) tabulated the uncertainty components in both their 147Sm α-activity measurements and their measurements of the number of 147Sm atoms in their counting sources, which together summed to 1.1% of the 147Sm half-life value, close to the figure of 0.9% uncertainty in the Kossert et al. (2009) determination, but considerably less than the ~2% obtained by Kinoshita, Yokoyama, and Nakanashi (2003). It would thus seem that the major reason for the difference between the Su et al. (2010) and Kinoshita, Yokoyama, and Nakanashi (2003) results may be due to the different Sm reagents used and the different procedures in preparing the counting sources.
Su et al. (2010) used 147Sm-enriched metal and Sm2O3 powder obtained from Oak Ridge National Laboratory and did not analyze them for purity, although they did perform isotope dilution mass spectrometry (IDMS) to check the 147Sm abundance, whereas Kinoshita, Yokoyama, and Nakanashi (2003) simply used commercially available Sm2O3 reagents and analyzed them for both impurities and the 147Sm abundance. Then Su et al. (2010) used vacuum evaporation (Sm metal) and sputtering (Sm2O3) to deposit the Sm reagents onto glass substrates to a thickness of about 250 μg/cm2 before checking the uniformity of 147Sm distribution in these prepared counting sources by exposure to plastic emulsions. On the other hand, Kinoshita, Yokoyama, and Nakanashi (2003) simply evaporated the prepared mixtures of Sm standard solutions and internal standards onto glass substrates adjusted to ~15 μg of 147Sm to ensure calculated amounts of α-particles would be measured from the 147Sm and internal standards in these prepared counting sources. However, neither the choice of Sm reagents nor the procedures in preparing the counting sources seem to be significantly different between these two 147Sm half-life determinations, even though Kinoshita, Yokoyama, and Nakanashi (2003) stated they prepared their counting sources in a manner different from earlier experiments. Apart from Su et al. (2010) not analyzing their chosen Sm reagents for purity, which would not be expected to be significant given the source of those reagents, the only major difference appears to have been the thicknesses of the counting sources and therefore the numbers of 147Sm atoms in them, resulting in only ~150 counts in the central channel of the α-peaks obtained by Kinoshita, Yokoyama, and Nakanashi (2003), the quite low activities in their experiments referred to by Kossert et al. (2009), compared to the 500–600 counts in the central channel of the α-peaks obtained by Su et al. (2010). Yet in spite of the lower α-activity, it could be argued that the thinner counting source should have yielded the more accurate determination of the 147Sm half-life value, because even though the thicker counting source would contain more 147Sm atoms and therefore emit more α-particles, the thicker the counting source the more self-absorption of α-particles there could be within the counting source thus significantly reducing the determined 147Sm half-life value.
If indeed the thicknesses of the counting sources and thus the self-absorption of α-particles in them have resulted in the experimentally determined values of the 147Sm half-life being up to 10% or more different, then this has profound significance on the determinations of the Sm-Nd radioisotope ages of rocks, minerals, and meteorites. Without certainty as to whether the present 147Sm half-life (decay rate) has been accurately determined experimentally by direct counting, and the assumption of constant radioisotope decay rates at the currently determined values, the Sm-Nd radioisotope ages calculated by uniformitarians cannot be accurately known, no matter how accurate are the measured 147Sm/144Nd and 143Nd/144Nd ratios in rocks, minerals, and meteorites.
In any case, the adopted 147Sm half-life value of 106 ± 0.8 Byr had essentially been already settled on the basis of the geological comparisons done on two meteorites by Lugmair, Scheinin, and Marti (1975) and Lugmair and Marti (1977) who adjusted these meteorites’ Sm-Nd ages to agree with their Pb-Pb ages (Begemann et al. 2001; Dickin 2005, 70–71). Lugmair (1974) compared the Sm-Nd isochron age he obtained for the Juvinas eucrite meteorite with the similar Rb-Sr isochron age obtained on the same meteorite by Allègre, Birck, and Fourcade (1973). However, it was Lugmair, Scheinin, and Marti (1975) whom Dickin (2005, 70–71) credited for the Sm-Nd isochron age of 4.56 ± 0.08 Byr for Juvinas that is in agreement with the Pb-Pb isochron age for the solar system and thus confirming the adopted value of 106 Byr for the 147Sm half-life (Dickin 2005, 115–118; Patterson 1956). This though begs the question— how do they know that these so-called isochrons are not mixing lines which have no time significance? It should also be noted that Dickin (2005, 71, fig. 4.1 caption) wrote that the “Nd isotope ratios are affected by the choice of normalizing factor for mass fractionation,” a reminder that the agreement of this Sm-Nd isochron age with the Pb-Pb isochron age was only achieved by making choices of suitable factors. Subsequently, Lugmair and Marti (1977) obtained a Sm-Nd isochron age of 4.55 ± 0.04 Byr for the Angra dos Reis (ADOR) angrite meteorite based on analyses of phosphate and pyroxene mineral separates, which they made sure agreed with the Pb-Pb model age of 4.555 ± 0.005 Byr for ADOR obtained by Tatsumoto, Knight, and Allègre (1973). Lugmair and Galer (1992) later refined that Pb-Pb model age for ADOR to 4.55780 ± 0.00042 Byr based on analyzing a pyroxene mineral separate, which they then used to suggest what the 147Sm half-life should be in order to make the Sm-Nd isochron age for this meteorite agree exactly with this Pb-Pb model age.
Lugmair and Marti (1977) and Lugmair and Galer (1992) justified their geological comparisons to adjust the 147Sm half-life value so that the Sm-Nd isochron ages of the Juvinas and Angra dos Reis meteorites agreed with their Pb-Pb isochron and model ages on the basis that these meteorites’ Pb-Pb ages were more precise because the decay constants of the parent 238U and 235U “are known more precisely.” And Lugmair and Marti (1978) added to the adoption of that 147Sm half-life value of 106 Byr by choosing the “most precise” results from only four of the earlier direct counting experiments (see table 1) that would give the desired weighted average value for the 147Sm half-life of 106 ± 0.8 Byr “that has been adopted by all geo- and cosmochronologists since that time” (Begemann et al. 2001). This was also the basis for Begemann et al. (2001) seeking to “correct” the Martins, Terranova, and Moreira Correa (1992) determined higher 147Sm half-life value to bring it into agreement with this adopted 147Sm half-life value calibrated against the U-Pb radioisotope system, and for Kossert et al. (2009) and Su et al. (2010) dismissing and ignoring respectively the more thoroughly determined but higher 147Sm half-life value of Kinoshita, Yokoyama, and Nakanashi (2003).
However, the U-Pb “gold standard” dating method has come under much scrutiny in the two last decades. Ludwig (2000) has demonstrated that, although almost universally ignored, the effect of the errors in the U decay constants on U-Pb concordia-Pb-Pb intercept ages are significant, being a 4.5 Myr error for a 500 Myr age, which amounts to almost a 1% error. The U-Pb method also depends on the crucial 238U/235U ratio, but discrepancies and variations have been found recently between the 238U/235U ratio in U-bearing terrestrial minerals and rocks and the 238U/235U ratio in meteorites (Brennecka and Wadhwa 2012; Hiess et al 2012). Much earlier, Apt et al. (1978) had reported that the 235U/238U ratio in uranium ores in Canada, Brazil, Zaire, and Australia varied from 0.7107 to 0.7144 when the recognized value is 0.72. Such variations in uranium ores have been further documented by Bopp et al. (2009). These discrepancies and variations remain unexplained, especially in the context of the 238U and 235U decay constants and half-lives. Furthermore, the fact that there are these variations in the crucial 238U/235U ratio in terrestrial minerals and rocks on which the U-Pb dating “gold standard” depends, which has been used to recalibrate Sm-Nd isochron ages to determine the 147Sm half-life and decay constant, only underscores that these radioisotope methods cannot provide the absolute invariable “dates” they are so confidently proclaimed to provide.
In any case, there is the additional assumption in all the radioisotope dating methods of having to know the original concentrations of the daughter and index isotopes which is very significant in the U-Pb method because the original concentrations are assumed not to be zero, in contrast to the K-Ar method. Yet there must be great uncertainty as to what those initial values were in the unobserved past, despite the isochron and concordia techniques attempting to negate the necessity for knowing those initial values, and despite the assumption ever since Patterson (1956) and Tatsumoto, Knight, and Allègre (1973) that the Pb isotopic composition of the troilite (FeS) in the Canyon Diablo iron meteorite represents the initial “primordial Pb” of the earth and the solar system (Dickin 2005; Faure and Mensing 2005). Thus the U-Pb method should not be used as a standard to determine other parent radioisotope half-lifes and decay constants.
Indeed, it would remain prudent to be very careful with these geological comparison methods for two other reasons. First, there are significant flaws in the basic assumptions on which all the radioisotope dating methods depend, not least being the assumption that the decay rates of the parent radioisotopes have always been constant in the past at today’s measured decay rates. Second, the U-Pb method relies primarily on α-decay, as does the Sm-Nd method. Yet both Austin (2005) and Snelling (2005) have reported that the parent U and Sm α-decaying radioisotopes seem to yield systematically different U-Pb and Sm-Nd ages for some earth rocks using the same samples with essentially the same methodology. Additionally, they suggested the pattern of differences was potentially related to the parent radioisotopes’ atomic weights and half-lives, which could be indicative of parent radioisotopes’ decay rates having not been constant in the past but instead were substantially faster. Furthermore, these different radioisotope ages yielded by the same earth rocks are often widely divergent, even up 100–200% different, which is such a huge divergence that it renders these dating methods highly suspect, even if the differences in the determinations of the half-lives of the parent radioisotopes seem miniscule and therefore trivial by comparison. However, it was considered prudent to still document here these seemingly miniscule differences in half-life values, because they may be indicative of other underlying factors at work (as already discussed briefly), and they can still lead to very significant discrepancies in the derived radioisotope ages that might otherwise appear to be acceptably accurate to uniformitarians.
Nevertheless, the age comparisons on meteorites used the U-Pb method back in the 1970s to settle, apparently beyond any subsequent dispute, the determination of the 147Sm decay half-life at 106 ± 0.8 Byr, which is within the range determined by many of the physical direct counting experiments by several techniques (see table 1 and fig. 2). Yet the robustness of the 10% higher 117 ± 2 Byr 147Sm half-life value determined by Kinoshita, Yokoyama, and Nakanashi (2003) might even indicate that the other higher 147Sm half-life values determined in some earlier experiments (see table 1 and fig. 2) should not be simply dismissed as due to poorer experimental methodology or equipment. In any case, Sm-Nd age calculations are now ultimately calibrated against the U-Pb method, and thus the 147Sm half-life value of 106 ± 0.8 Byr has been adopted. However, this U-Pb “gold standard” depends on whether the U decay constants are accurately and precisely known, and on the crucial 238U/235U ratio. Yet discrepancies and variations have been found between the 238U/235U ratio in U-bearing terrestrial minerals and rocks and the 238U/235U ratio in meteorites which remain unexplained. This only serves to highlight that if the Sm-Nd dating method has been calibrated against the U-Pb “gold standard” with its own uncertainties, then the claimed accurately-determined 147Sm decay rate cannot be absolute, especially given the evidence in some earth rocks of past higher radioisotope decay rates and the evidence that some direct counting experiments yielded 10% or more higher 147Sm half-life values. Yet even though it is to be expected these half-life measurements vary by 10% or so because of the difficulties in measuring such a long half-life, the resultant calculated radioisotope ages end up being an order of magnitude or more different from one another, which is far too “inaccurate” in providing the absolute ages required by uniformitarians. Thus without an accurately known 147Sm decay half-life, accurate Sm-Nd radioisotope ages cannot be accurately determined. Therefore, Sm-Nd dating cannot be used to reject the young-earth creationist timescale, especially as current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
Conclusions
There have been numerous attempts to determine the 147Sm decay half-life in the last 80 years by two primary techniques used in direct physical counting experiments—ionization chambers and liquid scintillation counters, and by radioisotope age comparisons using two meteorites. The determinations since 1960 have converged with close agreement on the 147Sm half-life value of 106 ± 0.8 Byr, which has since the 1970s been adopted for standard use by the uniformitarian geological community. This adopted 147Sm half-life value is the weighted average of four determinations by direct counting experiments in the period 1961–1970, confirmed by geological comparisons in the 1970s in which the 147Sm half-life value was adjusted in order to recalibrate (or force, essentially by circular reasoning) the Sm-Nd isochron ages of two meteorites to be the same as their Pb-Pb isochron and model ages.
However, even though this 147Sm half-life value of 106 ± 0.8 Byr has been universally adopted by the geochronology and cosmochronology community since Lugmair and Marti (1978) proposed it (Begemann et al. 2001), the more recent direct counting experiments by Kinoshita, Yokoyama, and Nakanashi (2003) determined the 147Sm half-life value was 10% or more longer at 117 ± 2 Byr. They achieved this by using four standard Sm solutions with internal α-radioactive standards in 19 alpha spectrometer and 24 ionization chamber determinations, making it the most thorough and comprehensive effort to the determine the 147Sm half-life. It would appear that the thinner counting sources they used, while resulting in low α-activities being measured, greatly reduced the counting uncertainty due to self-absorption of the emitted α-particles. So in spite of being rejected or ignored, this 117 ± 2 Byr value for the 147Sm half-life, which agrees with some earlier determinations, may well be highly significant and more reliable than the adopted value.
Yet even though there is close agreement between many determined values, the 147Sm half-life value obtained by recalibrating the Sm-Nd isochron ages for two meteorites with their Pb-Pb isochron and model ages has been given preference over the values obtained by direct counting experiments which directly measure 147Sm decay, and so are independent of all the assumptions involved with the radioisotope dating methods. Indeed, model dependent results should not take precedence over the direct experimental evidence.
Since the age comparisons on two meteorites used the U-Pb method to determine the 147Sm decay half-life, all Sm-Nd age calculations are thus ultimately calibrated against the U-Pb method. However, this U-Pb “gold standard” depends on having precisely determined 238U and 235U decay constants, as well as on the crucial 238U/235U ratio being known and constant. Yet there are still uncertainties in the measured U decay constants, and discrepancies and variations have been found between the 238U/235U ratio in U-bearing terrestrial minerals and rocks, and the 238U/235U ratio in meteorites. These discrepancies and variations remain unexplained. This only serves to highlight that if the Sm-Nd dating method has been calibrated against the U-Pb “gold standard” with its own uncertainties, then it cannot be absolute.
Furthermore, there is evidence that nuclear decay rates have not been constant in the past. Thus without an accurately known 147Sm decay half-life, accurate Sm-Nd radioisotope ages cannot be accurately determined. Therefore, Sm-Nd dating cannot be used to reject the young-earth creationist timescale, especially as current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
Acknowledgments
The invaluable help of my research assistant in compiling and plotting the data in the color-coded age diagrams is acknowledged. The three reviewers are also acknowledged for their helpful comments and input, though the final content of this paper is solely my responsibility. Our production assistant Laurel Hemmings is also especially thanked for her painstaking work in preparing this paper for publication.
References
Al-Bataina, B., and J. Jänecke. 1987. “Half-lives of Long-lived Alpha Emitters.” Radiochimica Acta 42 (4): 159–64.
Allègre, C. J., J. L. Birck, and S. Fourcade. 1973. “87Rb/87Sr Age of Juvinas Basaltic Achondrite and Early Igneous Activity in the Solar System.” Meteoritics 8: 323.
Apt, K. E., J. P. Balagna, E. A. Bryant, G. A. Cowan, W. R. Daniels, R. J. Vidale, and D. G. Brookins. 1978. “Search for Other Natural Fission Reactors.” In Natural Fission Reactors, Proceedings of a Meeting on Natural Fission Reactors, Paris, France, December 1977, IAEA-TC-119/37, 677–89. Vienna, Austria: International Atomic Energy Agency.
Austin, S. A. 2005. “Do Radioisotope Clocks Need Repair? Testing the Assumptions of Isochron Dating Using K-Ar, Rb-Sr, Sm-Nd, and Pb-Pb Isotopes.” In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 325–92. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/do-radioisotope-clocks-need-repair/.
Beard, G. B., and W. H. Kelly. 1958. “The Use of a Samarium Loaded Liquid Scintillator for the Determination of the Half-Life of Sm147.” Nuclear Physics 8: 207–09.
Beard, G. B., and M. L. Wiedenbeck. 1954. “Natural Radioactivity of Sm147.” Physical Review 95 (5): 1245–46.
Begemann, F., K. R. Ludwig, G. W. Lugmair, K. Min, L. E. Nyquist, P. J. Patchett, P. R. Renne, C.-Y. Shih, I. M. Villa, and R. J. Walker. 2001. “Call for an Improved Set of Decay Constants for Geochronological Use.” Geochimica et Cosmochimica Acta 65 (1): 111–21.
Bopp, C. J., C. C. Lundstrom, T. M. Johnson, and J. J. G. Glessner. 2009. “Variations in 238U/235U in Uranium Ore Deposits: Isotopic Signatures of the U Reduction Process?” Geology 37 (7): 611–14.
Brennecka, G. A., and M. Wadhwa. 2012. “Uranium Isotope Compositions of the Basaltic Angrite Meteorites and the Chronological Implications for the Early Solar System.” Proceedings of the National Academy of Sciences USA 109 (24): 9299–303.
Dempster, A. J. 1948. “The Alpha-Ray Emitting Isotope in Samarium.” Physical Review 73 (9): 1125–26.
Dickin, A. P. 2005. Radiogenic Isotope Geology. 2nd ed. Cambridge, United Kingdom: Cambridge University Press.
Donhoffer, D. 1964. “Bestimmung der Halbwertszeiten der in der Natur Vorkommenden Radioaktiven Nuklide Sm147 and Lu176 Mittels Flüssiger Szintillatoren.” Nuclear Physics 50: 489–96.
Faure, G., and T. M. Mensing. 2005. Isotopes: Principles and Applications. 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Graeffe, G., and M. Nurmia 1961. “The Use of Thick Sources in Alpha Spectrometry.” Annals of the Academy of Sciences of Fennoscandia A 6: 1–14.
Gupta, M. C., and R. D. MacFarlane. 1970. “The Natural Alpha Radioactivity of Samarium.” Journal of Inorganic and Nuclear Chemistry 32 (11): 3425–32.
Hiess, J., D. J. Condon, N. McLean, and S. R. Noble. 2012. “238U/235U Systematics in Terrestrial Uranium-Bearing Minerals.” Science 335 (6076): 1610–14.
Hosemann, V. R. 1936. “Die Radioaktivität des Samariums.” Zeitschrift für Physik 99 (5–6): 405–27.
Karras, M. 1960. “On the Natural Radioactivity of Samarium.” Annals of the Academy of Sciences of Fennoscandia A 6: 15–30.
Karras, M., and M. Nurmia. 1960. “Natural Radioactivity of Samarium and Neodymium.” Nature 185: 601.
Kinoshita, N., A. Yokoyama, and T. Nakanashi. 2003. “Half-Life of Samarium-147.” Journal of Nuclear Radiochemistry 4: 5–7.
Kossert, K., G. Jörg, O. Nähle, and C. L. von Gostomski. 2009. “High-Precision Measurement of the Half-Life of 147Sm.” Applied Radiation and Isotopes 67 (9): 1702–06.
Lide, D. R., and H. P. R. Frederikse. 1995. Handbook of Chemistry and Physics. 76th ed. Boca Raton, Florida: CRC Press.
Ludwig, K. R. 2000. “Decay Constant Errors in U-Pb Concordia- Intercept Ages.” Chemical Geology 166 (3–4): 315–18.
Lugmair, G. W. 1974. “Sm-Nd Ages: A New Dating Method.” Meteoritics 9: 369.
Lugmair, G. W., and S. J. G. Galer. 1992. “Age and Isotopic Relationships Among the Angrites Lewis Cliff 86010 and Angra dos Reis.” Geochimica et Cosmochimica Acta 56 (4): 1673–94.
Lugmair, G. W., and K. Marti. 1977. “Sm-Nd-Pu Timepieces in the Angra dos Reis Meteorite.” Earth and Planetary Science Letters 35 (2): 273–84.
Lugmair, G. W., and K. Marti. 1978. “Lunar Initial 143Nd/144Nd: Differential Evolution of the Lunar Crust and Mantle.” Earth and Planetary Science Letters 39 (3): 349–57.
Lugmair, G. W., N. B. Scheinin, and K. Marti. 1975. “Search of Extinct 146Sm, 1. The Isotopic Abundance of 142Nd in the Juvinas Meteorite.” Earth and Planetary Science Letters 27: 79–84.
MacFarlane, R. D., and T. P. Kohman. 1961. “Natural Alpha Radioactivity in Medium-Heavy Elements.” Physical Review 121 (6): 1758–69.
Martins, J. B., M. L. Terranova, and M. Moreira Correa. 1992. “Half-Life for Alpha-Decay of 147Sm.” Il Nuovo Cimento 105 (11): 1621–26.
Miller, J. L. 2012. “Time to Reset Isotopic Clocks? Two New Studies Revise Key Parameters in Radiometric Dating.” Physics Today 65 (6): 20–22.
Min K., R. Mundil, P. R. Renne, and K. R. Ludwig. 2000. “A Test for Systematic Errors in 40Ar/39Ar Geochronology Through Comparison with U-Pb Analysis of a 1.1 Ga Rhyolite.” Geochimica et Cosmochimica Acta 64 (1): 73–98.
Patterson, C. 1956. “Age of Meteorites and the Earth.” Geochimica et Cosmochimica Acta 10 (4): 230–37.
Picciotto, E. 1949. “Étude de la Radioactivité du Samarium par la Méthode Photographique.” Compte Rendus Hebdomadaires de Séances de l’Académie des Sciences 229: 117–19.
Renne, P. R., D. B. Karner, and K. R. Ludwig. 1998. “Absolute Ages Aren’t Exactly.” Science 282 (5395): 1840–41.
Schmitz, M. D. 2012. “Radiogenic Isotope Geochronology.” In The Geologic Time Scale 2012. Edited by F. M. Gradstein, J. G. Ogg, M. D. Schmitz, and G. M. Ogg, vol. 1, chap. 6, 115– 26. Amsterdam, The Netherlands: Elsevier.
Snelling, A. A. 2005. “Isochron Discordances and the Role of Mixing and Inheritance of Radioisotopes in the Mantle and Crust.” In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 393–524. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/isochron-discordances-role-inheritance/.
Snelling, A. A. 2014a. “Determination of the Radioisotope Decay Constants and Half-Lives: Rubidium-87 (87Rb).” Answers Research Journal 7: 311–22. https://answersingenesis.org/ geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rubidium-87-87Rb/.
Snelling, A. A. 2014b. “Determination of the Radioisotope Decay Constants and Half-Lives: Lutetium-176 (176Lu).” Answers Research Journal 7: 483–97. https://answersingenesis.org/ geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-lutetium-176/.
Snelling, A. A. 2015. “Determination of the Radioisotope Decay Constants and Half-Lives: Rhenium-187 (187Re).” Answers Research Journal 8: 93–111. https://answersingenesis.org/ geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rhenium-187/.
Steiger, R. H., and E. Jäger. 1977. “Subcommission on Geochronology: Convention on the Use of Decay Constants in Geo- and Cosmochronology.” Earth and Planetary Science Letters 36 (3): 359–62.
Su, J., Z. H. Li, L. C. Zhu, G. Lian, X. X. Bai, Y. B. Wang, B. Guo et al. 2010. “Alpha Decay Half-Life of 147Sm in Metal Samarium and Sm2O3.” The European Physical Journal A 46: 69–72.
Tatsumoto, M., R. J. Knight, and C. J. Allègre. 1973. “Time Differences in the Formation of Meteorites as Determined from the Ratio of Lead-207 to Lead-206.” Science 180 (4092): 1279–83.
Valli, K., J. Aaltonen, G. Graeffe, M. Nurmia, and R. Pöyhönen. 1965. “Half-Life of Sm-147: Comparison of Ionization and Liquid Scintillation Results.” Annals of the Academy of Science of Fennoscandia Series A 6: 177.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2000. Radioisotopes and the Age of the Earth: A Young-earth Creationist Research Initiative. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2005. Radioisotopes and the Age of the Earth: Results of a Young-earth Creationist Research Initiative. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/rate2/.
Wasserburg G. J., D. A. Papanastassiou, E. V. Nemov, and C. A. Bauman. 1969. “A Programmable Magnetic Field Mass Spectrometer with On-Line Data Processing.” Reviews of Scientific Instruments 40 (2): 288–95.
Weaver, B. 1950. “Mass Assignment of Natural Activity of Samarium.” Physical Review 80: 301.
Wilkins, T. R., and A. J. Dempster, 1938. “The Radioactive Isotope of Samarium.” Physical Review 54: 315.
Wright, P. M., E. P. Steinberg, and L. E. Glendenin. 1961. “The Half-Life of Samarium-147.” Physical Review 123 (1): 205– 208.












