The views expressed in this paper are those of the writer(s) and are not necessarily those of the ARJ Editor or Answers in Genesis.
Abstract
Meteorites date the earth with a 4.55 ± 0.07 Ga Pb-Pb isochron called the geochron. They appear to consistently yield 4.55–4.57 Ga radioisotope ages, adding to the uniformitarians’ confidence in the radioisotope dating methods. Achondrites, meteorites not containing chondrules, account for about 8% of meteorites overall. About 3% of the witnessed falls of all meteorite types are the achondrites known as eucrites, which makes them the fourth-most-common meteorite to fall. Eucrites are similar to basalts and are believed to be space debris from the crust of main belt asteroid 4-Vesta. Many radioisotope dating studies in the last 45 years have used the K-Ar, Ar-Ar, Rb-Sr, Sm-Nd, U-Th-Pb, Lu-Hf, Mn-Cr, Hf-W, Al-Mg, I-Xe, and Pu-Xe methods to yield an abundance of isochron and model ages for these basaltic achondrites from whole-rock samples, and mineral and other fractions. Such age data for 12 eucrites were tabulated and plotted on frequency versus age histogram diagrams. They strongly cluster in many of these eucrites at 4.55–4.57 Ga, dominated by Pb-Pb and U-Pb isochron and model ages, testimony to that technique’s supremacy as the uniformitarians’ ultimate dating tool, which they consider very reliable. These ages are confirmed by Rb-Sr, Lu-Hf, and Sm-Nd isochron ages, but agreement could be due to calibration with the Pb-Pb system. There is also scatter of the U-Pb, Pb-Pb, Th-Pb, Rb-Sr, K-Ar, and Ar-Ar model ages, in most cases likely due to thermal disturbances resulting from metamorphism or impact cratering of the parent asteroid. No pattern was found in these meteorites’ isochron ages similar to the systematic patterns of isochron ages found in Precambrian rock units during the RATE project, so there is no evidence of past accelerated radioisotope decay having occurred in these eucrites, and therefore on their parent asteroid. This is not as expected, yet it is the same for all meteorites so far studied. Thus it is argued that accelerated radioisotope decay must have only occurred on the earth, and only the 500–600 million years’ worth we have physical evidence for during the Flood. Otherwise, due to their 4.55–4.57 Ga “ages” these eucrites and their parent asteroid are regarded as originally representing “primordial material” that God made on Day One of the Creation Week, from which He made the non-earth portion of the solar system on Day Four, which is compatible with the Hebrew text of Genesis. Thus today’s measured radioisotope compositions of these eucrites could reflect a geochemical signature of that “primordial material,” which included atoms of all elemental isotopes. So if most of the measured daughter isotopes were already in these basaltic achondrites when they were formed on their parent asteroid, then their 4.55–4.57 Ga “ages” obtained by Pb-Pb and U-Pb isochron and model age dating are likely not their true real-time ages, which according to the biblical paradigm is only about 6000 real-time years. Further investigation of radioisotope ages data for meteorites in remaining groups of achondrites, for lunar rocks, and for rocks from every level in the earth’s geologic record, should enable the interim ideas presented here to be confirmed or modified.
Keywords: meteorites, classification, achondrites, eucrites, asteroids, 4-Vesta, radioisotope dating, Bereba, Cachari, Caldera, Camel Donga, Ibitira, Juvinas, Moama, Moore County, Pasamonte, Serra de Magé, Stannern, Yamato 75011, K-Ar, Ar-Ar, Rb-Sr, Sm-Nd, U-Th-Pb, Lu-Hf, Mn-Cr, Hf-W, Al-Mg, I-Xe, Pu-Xe, isochron ages, model ages, discordant radioisotope ages, accelerated radioactive decay, thermal disturbance, resetting, “primordial material,” geochemical signature, mixing, inheritance
Introduction
In 1956 Claire Patterson at the California Institute of Technology in Pasadena reported a Pb-Pb isochron age of 4.55 ± 0.07 Ga for three stony and two iron meteorites, which since then has been declared the age of the earth (Patterson 1956). Adding weight to that claim is the fact that many meteorites appear to consistently date to around the same “age” (Dalrymple 1991, 2004), thus bolstering the evolutionary community’s confidence that they have successfully dated the age of the earth and the solar system at around 4.56 Ga. These apparent successes have also strengthened their case for the supposed reliability of the increasingly sophisticated radioisotope dating methods.
Creationists have commented little on the radioisotope dating of meteorites, apart from acknowledging the use of Patterson’s geochron to establish the age of the earth, and that many meteorites give a similar old age. Morris (2007) did focus on the Allende carbonaceous chondrite as an example of a well-studied meteorite analyzed by many radioisotope dating methods, but he only discussed the radioisotope dating results from one, older paper (Tatsumoto, Unruh, and Desborough 1976).
In order to rectify this lack of engagement by the creationist community with the meteorite radioisotope dating data, Snelling (2014a) obtained as much radioisotope dating data as possible for the Allende CV3 carbonaceous chondrite meteorite (due to its claimed status as the most studied meteorite), displayed the data, and attempted to analyze them. He found that both isochron and model ages for the total rock, separated components, or combinations of these strongly clustered around a Pb-Pb age of 4.56–4.57 Ga, the earliest (Tatsumoto, Unruh, and Desborough 1976) and the latest (Amelin et al. 2010) determined Pb-Pb isochron ages at 4.553 ± 0.004 Ga and 4.56718 ± 0.0002 Ga respectively being essentially the same. Apart from scatter of the U-Pb, Th-Pb, Rb-Sr, and Ar-Ar ages, no systematic pattern was found in the Allende isochron and model ages similar to the systematic pattern of isochron ages found in Precambrian rock units during the RATE project that was interpreted as produced by an episode of past accelerated radioisotope decay (Snelling 2005c; Vardiman, Snelling, and Chaffin 2005).
Snelling (2014b) subsequently gathered together all the radioisotope ages obtained for 10 ordinary (H, L, and LL) and five enstatite (E) chondrites and similarly displayed the data. They generally clustered, strongly in the Richardton (H5), St. Marguerite (H4), Bardwell (L5), Bjurbole (L4), and St. Séverin (LL6) ordinary chondrite meteorites, at 4.55–4.57 Ga, dominated by Pb-Pb and U-Pb isochron and model ages, but confirmed by Ar-Ar, Rb-Sr, Re-Os, and Sm-Nd isochron ages. There was also scatter of the U-Pb, Th-Pb, Rb-Sr, and Ar-Ar model ages, in some cases possibly due to thermal disturbance. Again, no pattern was found in these meteorites’ isochron ages indicative of past accelerated radioisotope decay.
Snelling (2014a, b) then sought to discuss the possible significance of this clustering in terms of various potential creationist models for the history of radioisotopes and their decay. He favored the idea that asteroids and the meteorites derived from them are “primordial material” left over from the formation of the solar system, which is compatible with the Hebrew text of Genesis that could suggest God made “primordial material” on Day One of the Creation Week, from which He made the non-earth portion of the solar system on Day Four. Thus he argued that today’s measured radioisotope compositions of all these chondrites may reflect a geochemical signature of that “primordial material,” which included atoms of all elemental isotopes. So if some of the daughter isotopes were already in these chondrites when they were formed, then the 4.55–4.57 Ga “ages” for them obtained by Pb-Pb and U-Pb isochron and model age dating are likely not their true real-time ages, which according to the biblical paradigm is only about 6000 real-time years.
However, Snelling (2014a, b) admitted that drawing firm conclusions from the radioisotope dating data for just these 16 chondrite meteorites was premature, and recommended further studies of more meteorites. This present contribution is therefore designed to further document the radioisotope dating data for more meteorites, the basaltic achondrites or eucrites, so as to continue the discussion of the potential significance of these data.
The Classification of Achondrite Meteorites
The most recent classification scheme for the meteorites is that of Weisberg, McCoy, and Krot (2006), which is reproduced in Fig. 1. Based on their bulk compositions and textures, Krot et al. (2005) divided meteorites into two major categories, chondrites (meteorites containing chondrules) and achondrites (meteorites not containing chondrules or non-chondritic meteorites). They further subdivided the achondrites into primitive achondrites and igneously differentiated achondrites. However, Weisberg, McCoy, and Krot (2006) simply subdivided all meteorites into three categories—chondrites, primitive achondrites and achondrites (fig. 1).
The non-chondritic meteorites contain virtually none of the components found in chondrites. It is conventionally claimed that they were derived from chondritic materials by planetary melting, and that fractionation caused their bulk compositions to deviate to various degrees from chondritic materials (Krot et al. 2005). The degrees of melting that these rocks experienced are highly variable, and thus, these meteorites have been divided into the two major categories—primitive and differentiated. However, there is no clear cut boundary between these categories.
The differentiated non-chondritic meteorites, or achondrites (fig. 1), are conventionally regarded as having been derived from parent bodies that experienced large-scale partial melting, isotopic homogenization (ureilites are the only exception), and subsequent differentiation. Based on abundance of FeNi-metal, these meteorites are commonly divided into three types—achondrites, stony-irons, and irons. Each of these types contains several meteorite groups and ungrouped members (fig. 1). Several groups of achondrites and iron meteorites are likely to be genetically related and were possibly derived from single asteroids or planetary bodies.
The achondrites account for about 8% of meteorites overall, and the majority of them (about two-thirds) are HED meteorites (howardites, eucrites, and diogenites), believed to have originated from the crust of asteroid 4-Vesta (Norton 2002) (fig. 1). Other types include martian, lunar, and several types thought to originate from as-yet unidentified asteroids. These groups have been determined on the basis of, for example, their bulk Fe/Mn and 17O/18O ratios, which are thought to be characteristic “fingerprints” for each parent body (Mittlefehldt et al. 1998).
The achondrites represent the products of classical igneous processes acting on the silicate-oxide system of asteroidal bodies—partial to complete melting, differentiation, and magmatic crystallization (Mittlefehldt 2005). Iron meteorites represent the complimentary metal-sulfide system products of this process. Thus the achondrites consist of materials similar to terrestrial basalts and plutonic rocks, so they exhibit igneous textures, or igneous textures modified by impact and/or thermal metamorphism, and distinctive mineralogies indicative of igneous processes.
The HED meteorites are sometimes grouped with the angrites and aubrites (fig. 1) and termed the asteroidal achondrites, because of all having been differentiated on parent asteroidal bodies. The howardite-eucrite-diogenite (HED) meteorites have been traditionally classified into the one clan, because there is strong evidence they originated on the same parent body, the asteroid 4-Vesta (Binzel and Xu 1993; Consolmagno and Drake 1977; Drake 2001; Mandler and Elkins-Tanton 2013; McCord, Adams, and Johnson 1970; McSween et al. 2011; McSween et al. 2013, 2014; Righter and Drake 1997). This was one of the first links made between meteorites and an asteroid (Cloutis, Binzel, and Gaffey 2014; McCord, Adams, and Johnson 1970). Initially their spectroscopic similarity, which suggested the HED achondrites are impact ejecta off 4-Vesta, was deemed dynamically dubious owing to the apparent lack of a plausible pathway from Vesta to the earth. The discovery of the Vesta family of asteroids or “Vestoids” (Binzel and Xu 1993) extending from Vesta to resonance delivery zones solidified the link. This link has stood the test of time and has been confirmed by the in situ results provided by the Dawn mission to this asteroid (McSween et al. 2014). Thus the HED clan allows the confident association of specific types of igneous processes with an asteroid body of known size.
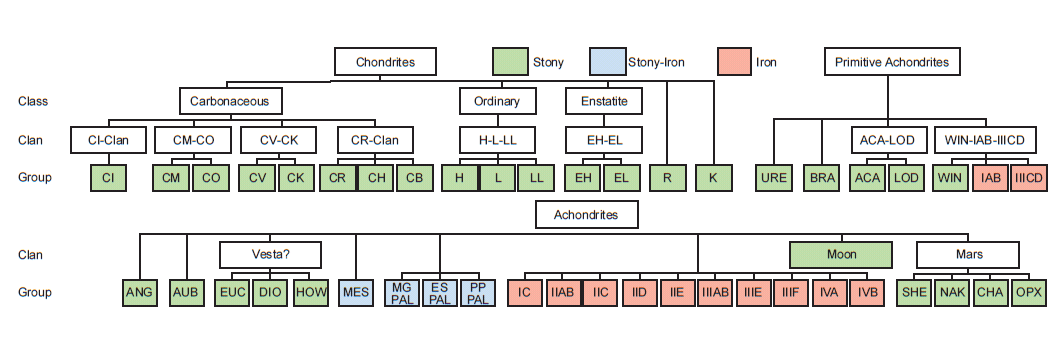
Fig. 1. The classification system for meteorites (after Weisberg, McCoy, and Krot 2006). (Click image for larger view.)
The HED clan is the most extensive suite of differentiated crustal rocks from an asteroid (Mittlefehldt 2005). Evidence that these achondrites belong in the same clan includes their identical oxygen isotopic compositions (Clayton and Mayeda 1996), similarities in Fe/Mn ratios in pyroxenes, the occurrence of polymict breccias consisting of materials of eucritic and diogenitic parentage (for example, the howardites), and the existence of rocks intermediate between diogenites and cumulate eucrites (Krot et al. 2005). The suite of meteorites comprising the HED clan is composed of mafic and ultramafic igneous rocks, most of which are breccias. The parent lithologies were mostly metamorphosed, which has obscured original igneous zoning in most cases (Mittlefehldt 2005). The suite contains four main igneous lithologies—basalt and cumulate gabbro (eucrites), and orthopyroxenite and harzburgite (diogenites). When both eucrite and diogenite clasts are present in a meteorite that is a polymict breccia, then it is a howardite. These lithologies are consistent with a postulated layered crust model for the HED parent body, 4-Vesta (Mandler and Elkins-Tanton 2013; McSween et al. 2013, 2014; Righter and Drake 1997; Takeda 1997).
The Eucrites
The eucrites are the most common of the achondrites. About 3% of the witnessed falls of all meteorite types are eucrites, which makes them the fourth most common meteorite to fall (Norton 2002). Of the HED meteorites, eucrites are by far the most common, about 52%. Until the meteorite finds in Antarctica became available with their large cache of eucrites, eucrites were defined as monomict breccias. However, the large number of eucrites recovered that show a wide variation of lithic fragments, unlike the fragments in howardites, has prompted the acceptance of eucrites as either monomict or polymict.
The most obvious external characteristic of a freshly fallen eucrite is its very black and lustrous fusion crust compared to the dull black crust of a chondrite, due to the intense heating of the outer surface during passage through the earth’s atmosphere (Norton 2002). Eucrites are Ca-rich and this combined with the usually present small amount of Fe gives these meteorites a “wet” look (fig. 2). Fusion crusts form in the final second or two of the ablation process as meteorites pass rapidly through the earth’s atmosphere during the fireball stage. The fusion crusts then rapidly cool, so contraction cracks often form, leaving the outer surface of the meteorites looking much like the crazing on pottery (figs. 2 and 3).

Fig. 2. The shiny black crust on this eucrite from Camel Donga, Western Australia, is typical of calcium-rich eucrites. Note the contraction cracks through the crust. The specimen measures 5 cm (about 2 in) in its longest dimension (after Norton 2002). (Click image for larger view.)

Fig. 3. Contraction cracks in the crust of the Pasamonte eucrite. The specimen is about 6.2 cm (about 2.5 in) long (after Norton 2002). (Click image for larger view.)

Fig. 4. This unbrecciated eucrite called Ibitira fell in the village of that name near Martinho Campos, Minas Gerais, Brazil, in 1957. It is the only eucrite known to have a vesicular texture. The millimeter-sized gas holes cover 5–7 vol. % of the rock. The scale rule is in cm so the specimen is about 10 cm (about 4 in) wide (after Norton 2002). (Click image for larger view.)
The similarities of eucrites chemically and petrographically to terrestrial basalts is frequently noted, but a broken face of a eucrite exposes a light gray interior, which is unlike the dark gray to black interiors of terrestrial basalts. Eucrite textures are also fine-grained, and often glomeroporphyritic due to clumps of phenocrysts set in the groundmass. This is typical of terrestrial volcanic rocks that have cooled more slowly, producing glomerocrysts of interlocking plagioclase and pyroxene crystals. If basaltic lava contains dissolved gases when it suddenly erupts onto the earth’s surface, the sudden reduction in pressure releases the gases which quickly form bubbles that make their way to the top of the flow. The eucrite, Ibitira, one of the few unbrecciated eucrites known, shows a remarkable vesicular texture (fig. 4), similar to that seen in a terrestrial basalt lava flow as that just described. Microscopically, the resemblance of most eucrites to terrestrial basalts is also most striking (fig. 5a and b).
Fig. 5. Thin section photomicrographs in transmitted light under crossed polars of four typical eucrites (basaltic achondrites) (after Krot et al. 2005; McSween et al. 2011).

(a) The unequilibrated noncumulate eucrite Pasamonte, showing the typical basaltic texture of plagioclase (light) and pyroxene (colored). (Click image for larger view.)

(b) The metamorphosed (equilibrated) noncumulate eucrite Ibitira, showing a recrystallized texture with plagioclase (white) and pyroxene (colored), with the round, dark areas in the center, bottom, and left being vesicles. (Click image for larger view.)

(c) The cumulate eucrite Serra de Magé, consisting of large crystals of plagioclase (lighter material with straight twin lamellae) and mostly orthopyroxene with complex augite exsolution lamellae (darker material with irregular, sometimes worm-like exsolution lamellae). (Click image for larger view.)

(d) The cumulate eucrite Moore County, consisting of large crystals of plagioclase (lighter material with straight twin lamellae) and colorful abundant orthopyroxene (with occasional exsolution lamellae) (scale bar is 2.5mm [0.09in]).
Mineralogically, the eucrites are quite simple. They consist almost entirely of plagioclase (30–50%) and clinopyroxene (40–60%), the clinopyroxene usually dominating by 10–20%. The plagioclase in eucrites is calcic, being primarily anorthite with some bytownite, that is, within the range An75-95, and igneous zoning is commonly preserved. The clinopyroxene is low-Ca pigeonite, with a composition that varies widely from specimen to specimen, and even within a given specimen. A typical pyroxene composition (wollastonite-enstatite-ferrosilite) in mole percent might be Wo1-25 En42-48 Fs43-52. Minor minerals include chromite (FeCr2O4), Fe-Ni metal, ilmenite (FeTiO3) and troilite (FeS) as opaque minerals, orthopyroxene, and polymorphs of silica—quartz, tridymite, and cristobalite.
Eucrites are subdivided into three major subclasses—the noncumulate eucrites (basaltic eucrites), the cumulate eucrites (cumulate gabbros), and the polymict eucrites (polymict breccias of basaltic and cumulate eucrites) (Krot et al. 2005; Mittlefehldt 2005).
Noncumulate (basaltic) eucrites are mostly fragmental breccias of fine to medium grained, subophitic to ophitic basalts that are postulated to have formed originally as quickly cooled surface lava flows. They are known as unequilibrated, unmetamorphosed or least-metamorphosed, noncumulate eucrites (such as Pasamonte—see fig. 5a), and are composed of pigeonite and plagioclase, with minor silica, ilmenite, and chromite, and accessory phosphates, troilite, Fe-Ni metal, fayalitic olivine, zircon, and baddeleyite. As a result of their apparent fast cooling their pyroxenes (pigeonite of Mg# ~70–20) are zoned, and exsolution lamellae are only visible by TEM. However, most noncumulate eucrites appear to have been subsequently metamorphosed, and are thus known as metamorphosed or equilibrated noncumulate eucrites (such as Juvinas, Stannern, and Ibitira—see fig. 5b). They are highly abundant and so are also collectively referred to as the ordinary eucrites. They are unbrecciated or monomict-brecciated, metamorphosed basalts and contain homogeneous low-Ca pigeonite (Mg# ~42–30) with fine exsolution lamellae of high-Ca pyroxene. The pyroxenes were originally ferroan pigeonite (~Wo7-15 En29-43 Fs48-58) which exsolved augite during metamorphism. In most eucrites, pyroxene Fe/Mg is uniform as a result of metamorphism, but original igneous zoning is preserved in very few. Plagioclase is calcic, with most in the range An75-93, and igneous zoning is commonly preserved.
Cumulate eucrites are coarse-grained gabbros, many unbrecciated (such as Serra de Magé—see fig. 5c, and Moore County—see fig. 5d), composed of pigeonite, plagioclase, and minor chromite with silica, ilmenite, Fe-Ni metal, troilite, and phosphate as trace accessory phases. The original igneous pyroxene was pigeonite (~Wo7-16 En38-61 Fs32-46) which exsolved augite and, in some, inverted to orthopyroxene. They contain orthopyroxene inverted from low-Ca clinopyroxene (Mg# ~67–58) and orthopyroxene inverted from pigeonite (Mg# ~57–45). Plagioclase is generally more calcic than that typical for basaltic eucrites, with most in the range An91-95.
Polymict eucrites are polymict breccias consisting of fragmental and melt-matrix breccias mostly of eucritic material, but they also contain <10 vol.% of diogenitic component in the form of orthopyroxenite.
The Radioisotope Dating of the Eucrites
To thoroughly investigate the radioisotope dating of the eucrite achondrites all the relevant literature was searched. The objective was to find eucrite achondrites that have been dated by more than one radioisotope method, and a convenient place to start was Dalrymple (1991, 2004), who compiled lists of such data. The 12 eucrite achondrite meteorites that were found to have been dated multiple times by more than one radioisotope method—Bereba, Cachari, Caldera, Camel Donga (fig. 2), Ibitira (figs. 4 and 5b), Juvinas, Moama, Moore County (fig. 5d), Pasamonte (figs. 3 and 5a), Serra de Magé (fig. 5c), Stannern, and Yamato 75011—thus became the focus of this study. When papers containing radioisotope dating results for these eucrites were found, the reference lists were also scanned to find further relevant papers. In this way a comprehensive set of papers, articles, and abstracts on radioisotope dating of these basaltic achondrite meteorites was collected. While it cannot be claimed that all the papers, articles, and abstracts which have ever been published containing radioisotope dating results for these eucrites have thus been obtained, the cross-checking undertaken between these publications does indicate the data set obtained is very comprehensive.
All the radioisotope dating results of these 12 eucrites were then compiled and tabulated. For ease of viewing and comparing the radioisotope dating data, the isochron and model ages for some or all components of each of these 12 eucrites were tabulated separately—the isochron ages in Table 1 and the model ages in Table 2. The data in these tables were then plotted on frequency versus age histogram diagrams, with the same color coding being used to show the ages obtained by the different radioisotope dating methods—the isochron ages for whole-rock samples and some or all components of each of these 12 eucrites (fig. 6), and the model ages for whole-rock samples and components of each of these 12 eucrites (fig. 7).
Table 1. Isochron ages for whole-rock samples and some or all components of 12 eucrite achondrites, with the details and literature sources.
| Sample | Method | Date | Err +/- | Note | Source | Type |
| Bereba | ||||||
| eight fractions (whole rock and mineral) | Rb-Sr | 4.17 | 0.26 | Birck and Allègre 1978 | isochron age | |
| Rb-Sr | 4.08 | 0.26 | Basaltic Volcanism Study Project 1981 | isochron age | ||
| one whole-rock sample plotted with 12 other samples | Rb-Sr | 4.55 | 0.19 | ten other meteorites plus three plagioclase samples | Hans, Kleine, and Bourdon 2013 | isochron age |
| one sample plotted with 14 other meteorites | Lu-Hf | 4.604 | 0.039 | Blichort-Toft et al. 2002 | isochron age | |
| whole rock and plagioclase samples | Pb-Pb | 4.522 | 0.004 | Carlson, Tera, and Boctor 1988 | isochron age | |
| plagioclase and whole rock + leachate | Pb-Pb | 4.52 | Tera, Carlson, and Boctor 1997 | isochron age | ||
| three zircon grains intercept concordia | U-Pb | 4.538 | 0.026 | Lee et al. 2009 | isochron age | |
| three point analyses of one apatite grain | U-Pb | 4.196 | 0.013 | Zhou et al. 2011 | isochron age | |
| five point analyses of three zircon grains | U-Pb | 4.552 | 0.021 | Zhou et al. 2013 | isochron age | |
| whole rock + mineral separates | Sm-Nd | 4.79 | Carlson, Tera, and Boctor 1988 | isochron age | ||
| one sample plotted with 17 other meteorites | Sm-Nd | 4.464 | 0.075 | Blichort-Toft et al. 2002 | isochron age | |
| one sample plotted with seven other meteorites | Hf-W | 4.5632 | 0.0014 | Kleine et al. 2004 | isochron age | |
| Hf-W | 4.55 | 0.0041 | Kleine et al. 2005 | isochron age | ||
| Cacheri | ||||||
| one sample plotted with 17 other meteorites | Lu-Hf | 4.604 | 0.039 | Blichort-Toft et al. 2002 | isochron age | |
| mean of three isochrons | Pb-Pb | 4.453 | 0.015 | Tera, Carlson, and Boctor 1997 | isochron age | |
| six fractions | 206Pb-204Pb | 4.453 | 0.015 | Tera, Carlson, and Boctor 1997 | isochron age | |
| eight fractions | 207Pb-206Pb | 4.451 | 0.015 | Tera, Carlson, and Boctor 1997 | isochron age | |
| eight fractions | 207Pb-204Pb | 4.455 | 0.016 | Tera, Carlson, and Boctor 1997 | isochron age | |
| sixteen analyses of six zircon grains | 207Pb-204Pb | 4.558 | 0.025 | Zhou et al. 2013 | isochron age | |
| three analyses of one zircon grain | U-Pb | 4.546 | 0.01 | Zhou et al. 2011 | isochron age | |
| three analyses of one zircon grain | U-Pb | 4.548 | 0.024 | Zhou et al. 2013 | isochron age | |
| six fractions | Sm-Nd | 3.99 | 0.21 | Tera, Carlson, and Boctor 1997 | isochron age | |
| one sample plotted with 17 other meteorites | Sm-Nd | 4.464 | 0.075 | Blichort-Toft et al. 2002 | isochron age | |
| Caldera | ||||||
| one whole-rock sample plotted with 14 other meteorites | Lu-Hf | 4.604 | 0.039 | Blichert-Toft et al. 2002 | isochron age | |
| pyroxene and plagioclase fractions | Pb-Pb | 4.5161 | 0.0028 | Galer and Lugmair 1996 | isochron age | |
| four points on one zircon grain | U-Pb | 4.563 | 0.18 | Zhou et al. 2013 | isochron age | |
| two whole rocks, plagioclase, and pyroxene fractions | Sm-Nd | 4.544 | 0.019 | Wadhwa and Lugmair 1996 | isochron age | |
| four fractions | Mn-Cr | 4.545 | Lugmair and Shukolyukov 1998 | isochron age | ||
| Camel Donga | ||||||
| matrix samples with pyroxenes, inverse | Ar-Ar | 3.706 | 0.097 | Kennedy et al. 2013 | isochron age | |
| matrix samples with pyroxenes, inverse | Ar-Ar | 3.685 | 0.085 | Kennedy et al. 2013 | isochron age | |
| mean of two, inverse | Ar-Ar | 3.703 | 0.059 | Kennedy et al. 2013 | isochron age | |
| thirty-five point analyses of 14 zircon grains | U-Pb | 4.512 | 0.011 | Zhou et al. 2013 | isochron age | |
| Hf-W | 4.546 | 0.005 | Kleine et al. 2005 | isochron age | ||
| Hf-W | 4.545 | 0.0035 | Kleine et al. 2005 | isochron age | ||
| Ibitira | ||||||
| whole rock plus four mineral separates | Rb-Sr | 4.52 | 0.25 | Birck and Allègre 1978 | isochron age | |
| Ibitira samples plotted with Juvinas samples, plus whole-rock samples of eight other meteorites | Rb-Sr | 4.57 | 0.13 | Birck and Allègre 1978 | isochron age | |
| one sample plotted with 14 other meteorites | Lu-Hf | 4.604 | 0.039 | Blichert-Toft et al. 2002 | isochron age | |
| three whole-rock samples | 207Pb-206Pb | 4.556 | Chen and Wasserburg 1985 | isochron age | ||
| nine samples (pyroxenes)—external normalization (EN) | 207Pb-206Pb | 4.55703 | 0.00082 | Amelin, Wadhwa, and Lugmair 2006 | isochron age | |
| nine samples (pyroxenes)—EN and double spike (DS) | 207Pb-206Pb | 4.55744 | 0.00055 | Amelin, Wadhwa, and Lugmair 2006 | isochron age | |
| pyroxene leachates and residues | Pb-Pb | 4.5561 | 0.0023 | Iizuka et al. 2013 | isochron age | |
| residues of eight pyroxene-rich and two whole-rock fractions and washes of two pyroxene-rich and one plagioclase-rich fractions(13-point isochron) | Pb-Pb | 4.5565 | 0.0013 | Iizuka et al. 2014 | isochron age | |
| residues of one whole-rock and six pyroxene-rich fractions (7-point isochron) | Pb-Pb | 4.55675 | 0.00057 | Iizuka et al. 2014 | isochron age | |
| residues of eight pyroxene-rich and two whole-rock fractions and washes of two pyroxene-rich and one plagioclase-rich fractions (13-point chord) | U-Pb | 4.5569 | 0.0014 | Iizuka et al. 2014 | isochron age (concordia) | |
| residues of one whole-rock and six pyroxene-rich fractions (7-point chord) | U-Pb | 4.556 | 0.0052 | Iizuka et al. 2014 | isochron age (concordia) | |
| whole rock plus five mineral separates | Sm-Nd | 4.46 | 0.02 | Prinzhofer, Papanastassiou, and Wasserburg 1992 | isochron age | |
| two whole-rock samples plus multiple plagioclase, pyroxene and phosphate separates | Sm-Nd | 4.57 | 0.09 | Nyquist et al. 1999 | isochron age | |
| two whole-rock samples plus phosphate and pyroxene separates | Sm-Nd | 4.6 | 0.05 | Nyquist et al. 1999 | isochron age | |
| two whole-rock samples plus pyroxene and plagioclase separates | Sm-Nd | 4.41 | 0.07 | Nyquist et al. 1999 | isochron age | |
| one sample plotted with 17 other meteorites | Sm-Nd | 4.464 | 0.075 | Blichert-Toft et al. 2002 | isochron age | |
| three fractions | Hf-W | 4.549 | 0.012 | Kleine et al. 2005 | isochron age | |
| three fractions | Mn-Cr | 4.557 | 0.003 | Lugmair and Shukolyukov 1998 | isochron age | |
| after Lugmair and Shukolyukov (1998) using Pb-Pb age of D’Orbigny | Mn-Cr | 4.5574 | 0.0025 | Iizuka et al. 2014 | isochron age | |
| after Yin, Amelin, and Jacobsen (2009) using the Pb-Pb age of D’Orbigny | Mn-Cr | 4.5559 | 0.0032 | Iizuka et al. 2014 | isochron age | |
| whole rock, pyroxene (2) and plagioclase (2) fractions | Al-Mg | 4.5614 | Wadhwa et al. 2004 | isochron age | ||
| whole rock, pyroxene (2) and plagioclase (2) fractions | Al-Mg | 4.5607 | Amelin, Wadhwa, and Lugmair 2006 | isochron age | ||
| relative to Shallowater | I-Xe | 4.555 | 0.001 | Claydon, Crowther, and Gilmour 2013 | isochron age | |
| Juvinas | ||||||
| one whole-rock sample plotted with six other meteorites | Rb-Sr | 4.39 | 0.26 | Papanastassiou and Wasserburg 1969 | isochron age | |
| four mineral separates plus whole rock | Rb-Sr | 4.6 | 0.07 | Allègre et al. 1975 | isochron age | |
| earlier data plotted with Ibitira | Rb-Sr | 4.58 | 0.14 | Birck and Allègre 1978 | isochron age | |
| revised Allègre et al. (1975) age | Rb-Sr | 4.5 | 0.07 | Quitte, Birck, and Allègre 2000 | isochron age | |
| whole-rock and plagioclase samples plotted with eleven other samples | Rb-Sr | 4.55 | 0.19 | ten other meteorites and two plagioclase samples | Hans, Kleine, and Bourdon 2013 | isochron age |
| one sample plotted with nine other meteorites | Lu-Hf | 4.55 | adjusted to agree with other methods | Patchett and Tatsumoto 1980 | isochron age | |
| one sample plotted with 14 other meteorites | Lu-Hf | 4.604 | 0.039 | Blichert-Toft et al. 2002 | isochron age | |
| pyroxene and plagioclase fractions | Pb-Pb | 4.3209 | 0.017 | Galer and Lugmair 1996 | isochron age | |
| 207Pb-206Pb | 4.556 | 0.012 | eight samples | Tatsumoto and Unruh 1975 | isochron age | |
| 207Pb-206Pb | 4.54 | 0.0007 | nine samples | Manhes, Allègre, and Provost 1984 | isochron age | |
| 206Pb-238U | 4.531 | 0.003 | upper intercept | Manhes, Allègre, and Provost 1984 | isochron age | |
| 206Pb-238U | 4.539 | 0.004 | upper intercept | Manhes, Allègre, and Provost 1984 | isochron age | |
| 206Pb-238U | 4.545 | 0.0012 | seven samples | Manhes, Allègre, and Provost 1984 | isochron age | |
| 207Pb-235U | 4.543 | 0.003 | eight samples | Manhes, Allègre, and Provost 1984 | isochron age | |
| 232Th-208Pb | 4.47 | 0.03 | nine samples | Manhes, Allègre, and Provost 1984 | isochron age | |
| twenty analyses of seven zircon grains | U-Pb | 4.53 | 0.033 | Zhou et al. 2013 | isochron age | |
| whole rock (2), plagioclase, and pyroxene fractions | Sm-Nd | 4.56 | 0.08 | Lugmair 1974; Lugmair, Scheinin, and Marti 1975 | isochron age | |
| one sample plotted with 17 other meteorites | Sm-Nd | 4.464 | 0.075 | Blichert-Toft et al. 2002 | isochron age | |
| five samples plotted with seven other meteorites | Hf-W | 4.5632 | 0.0014 | Kleine et al. 2004 | isochron age | |
| Hf-W | 4.5457 | 0.0036 | five fractions | Kleine et al. 2005 | isochron age | |
| five fractions | Mn-Cr | 4.5625 | 0.001 | Lugmair and Shukloyukov 1998 | isochron age | |
| Mn-Cr | 4.5642 | 0.0012 | Schiller, Baker, and Bizzarro 2010 | isochron age | ||
| whole rock, pyroxene (3), and plagioclase (3) fractions | Al-Mg | 4.561 | Wadhwa et al. 2004 | isochron age | ||
| Moama | ||||||
| whole-rock sample plotted with 12 other samples | Rb-Sr | 4.55 | 0.19 | ten other meteorites and three plagioclase samples | Hans, Kleine, and Bourdon 2013 | isochron age |
| one sample plotted with nine other meteorites | Lu-Hf | 4.55 | Patchett and Tatsumoto 1980 | isochron age | ||
| one sample plotted with 14 other meteorites | Lu-Hf | 4.604 | 0.039 | Blichert-Toft et al. 2002 | isochron age | |
| whole rock, WR leachate, and plagioclase and pyroxene separates | 207Pb-206Pb | 4.439 | 0.097 | Tera, Carlson, and Boctor 1997 | isochron age | |
| whole rock, WR leachate, and plagioclase and pyroxene separates | 207Pb-204Pb | 4.416 | 0.092 | Tera, Carlson, and Boctor 1997 | isochron age | |
| whole rock, WR leachate, and plagioclase and pyroxene separates | 206Pb-204Pb | 4.423 | 0.094 | Tera, Carlson, and Boctor 1997 | isochron age | |
| mean of the Pb-Pb isochron ages | mean Pb-Pb | 4.426 | 0.094 | Tera, Carlson, and Boctor 1997 | isochron age | |
| Sm-Nd | 4.52 | 0.05 | Hamet et al. 1978 | isochron age | ||
| whole rock, plus two pyroxene and plagioclase separates | Sm-Nd | 4.46 | 0.03 | Jacobsen and Wasserburg 1984 | isochron age | |
| whole rock, pyroxene and plagioclase fractions | Sm-Nd | 4.594 | 0.079 | plus Hamet et al. 1978 and Jacobsen and Wasserburg 1984 data | Boyet, Carlson, and Horan 2010 | isochron age |
| Moore County | ||||||
| one sample plotted with eight other meteorites | Rb-Sr | 4.557 | 0.253 | Cumming 1969 | isochron age | |
| one whole-rock sample plotted with six other meteorites | Rb-Sr | 4.39 | 0.26 | Papanastassiou and Wasserburg 1969 | isochron age | |
| plagioclase sample plotted with 12 other samples | Rb-Sr | 4.55 | 0.19 | ten other meteorites and two plagioclase samples | Hans, Kleine, and Bourdon 2013 | isochron age |
| one sample plotted with nine other meteorites and adjusted to agree with other methods | Lu-Hf | 4.55 | Patchett and Tatsumoto 1980 | isochron age | ||
| one sample plotted with 14 other meteorites | Lu-Hf | 4.604 | 0.039 | Blichert-Toft et al. 2002 | isochron age | |
| whole rock (3), pyroxene (2) and plagioclase (2) fractions and leachates | 207Pb-204Pb | 4.477 | 0.022 | Tera, Carlson, and Boctor 1997 | isochron age | |
| 207Pb-206Pb | 4.494 | 0.017 | isochron age | |||
| 206Pb-204Pb | 4.481 | 0.02 | isochron age | |||
| mean Pb-Pb | 4.484 | 0.019 | isochron age | |||
| internal Sm-Nd | 4.6 | 0.04 | Unruh, Nakamura, and Tatsumoto 1977 | isochron age | ||
| whole rock, pyroxene plagioclase (2) fractions | Sm-Nd | 4.456 | 0.025 | Tera, Carlson, and Boctor 1997 | isochron age | |
| Sm-Nd | 4.457 | 0.025 | Tera, Carlson, and Boctor 1997 | isochron age | ||
| one sample plotted with 17 other meteorites | Sm-Nd | 4.464 | 0.075 | Blichert-Toft et al. 2002 | isochron age | |
| whole rock, pyroxene and plagioclase fractions | Sm-Nd | 4.542 | 0.085 | plus Tera, Carlson, and Boctor 1997 and Blichert-Toft et al. 2002 data | Boyet, Carlson, and Horan 2010 | isochron age two |
| fractions | Mn-Cr | 4.549 | Lugmair and Shukolyukov 1998 | isochron age | ||
| Pasamonte | ||||||
| one sample plotted with five other meteorites | Rb-Sr | 4.411 | 0.088 | Shields, Pinson, and Hurley 1965 | isochron age | |
| one sample plotted with eight other meteorites | Rb-Sr | 4.557 | 0.253 | Cumming 1969 | isochron age | |
| one whole-rock sample plotted with six other meteorites | Rb-Sr | 4.39 | 0.26 | Papanastassiou and Wasserburg 1969 | isochron age | |
| two whole-rock samples plotted with nine other meteorites | Rb-Sr | 4.33 | 0.49 | Birck and Allègre 1978 | isochron age | |
| whole-rock sample plotted with 12 other samples | Rb-Sr | 4.55 | 0.19 | ten other meteorites and three plagioclase samples | Hans, Kleine, and Bourdon 2013 | isochron age |
| one sample plotted with nine other meteorites and adjusted to agree with other methods | Lu-Hf | 4.55 | Patchett and Tatsumoto 1980 | isochron age | ||
| one sample plotted with 14 other meteorites | Lu-Hf | 4.604 | 0.039 | Blichert-Toft et al. 2002 | isochron age | |
| revised Unruh, Nakamura, and M. Tatsumoto 1977 age | Pb-Pb | 4.573 | 0.011 | Quitté, Birck, and Allègre 2000 | isochron age | |
| whole rock and 13 mineral separates | 207Pb-206Pb | 4.53 | 0.03 | Unruh, Nakamura, and Tatsumoto 1977 | isochron age | |
| six sample points (whole-rock, plag, and density fractions) | Sm-Nd | 4.58 | 0.12 | Unruh, Nakamura, and Tatsumoto 1977 | isochron age | |
| two samples plotted with seven other meteorites | Hf-W | 4.5632 | 0.0014 | Kleine et al. 2004 | isochron age | |
| Serra De Magé | ||||||
| whole-rock sample plotted with 12 other samples | Rb-Sr | 4.55 | 0.19 | ten other meteorites and three plagioclase samples | Hans, Kleine, and Bourdon 2013 | isochron age |
| one sample plotted with nine other meteorites and adjusted to agree with other methods | Lu-Hf | 4.55 | Patchett and Tatsumoto 1980 | isochron age | ||
| one sample plotted with 14 other meteorites | Lu-Hf | 4.604 | 0.039 | Blichert-Toft et al. 2002 | isochron age | |
| whole rock, two whole rock leachates, and pyroxene and plagioclase fractions | 207Pb-204Pb | 4.406 | 0.045 | Tera, Carlson, and Boctor 1997 | isochron age | |
| 207Pb-206Pb | 4.39 | 0.016 | Tera, Carlson, and Boctor 1997 | isochron age | ||
| 206Pb-204Pb | 4.4 | 0.037 | Tera, Carlson, and Boctor 1997 | isochron age | ||
| mean Pb-Pb | 4.399 | 0.035 | Tera, Carlson, and Boctor 1997 | isochron age | ||
| Sm-Nd | 4.41 | 0.02 | Lugmair, Scheinin, and Carlson 1977 | isochron age | ||
| one sample plotted with 17 other meteorites | Sm-Nd | 4.464 | 0.075 | Blichert-Toft et al. 2002 | isochron age | |
| one sample plotted with seven other meteorites | Hf-W | 4.5632 | 0.0014 | Kleine et al. 2004 | isochron age | |
| three fractions | Mn-Cr | 4.553 | 0.003 | Lugmair and Shukolyukov 1998 | isochron age | |
| Stannern | ||||||
| one whole-rock sample plotted with six other meteorites | Rb-Sr | 4.39 | 0.26 | Papanastassiou and Wasserburg 1969 | isochron age | |
| eight fractions (whole-rock, three plagioclase, pyroxene, plus three others) | Rb-Sr | 3.3 | 0.5 | Birck and Allègre 1978 | isochron age | |
| whole-rock sample plotted with 12 other samples | Rb-Sr | 4.55 | 0.19 | ten other meteorites and three plagioclase samples | Hans, Kleine, and Bourdon 2013 | isochron age |
| two samples plotted with nine other meteorites | Lu-Hf | 4.55 | 0.019 | Patchett and Tatsumoto 1980 | isochron age | |
| one sample plotted with 14 other meteorites | Lu-Hf | 4.604 | 0.039 | Blichert-Toft et al. 2002 | isochron age | |
| three-point isochron based on whole-rock, pyroxene, and plagioclase fractions | 207Pb-204Pb | 4.131 | 0.012 | Tera, Carlson, and Boctor 1997 | isochron age | |
| 207Pb-206Pb | 4.124 | 0.023 | isochron age | |||
| 206Pb-204Pb | 4.13 | 0.012 | isochron age | |||
| mean Pb-Pb | 4.128 | 0.016 | isochron age | |||
| Sm-Nd | 4.48 | 0.07 | Lugmair and Scheinin 1975 | isochron age | ||
| one sample plotted with 17 other meteorites | Sm-Nd | 4.464 | 0.075 | Blichert-Toft et al. 2002 | isochron age | |
| whole rock, magnetic, and two non-magnetic fractions | Hf-W | 4.564 | 0.002 | Kleine et al. 2005 | isochron age | |
| Yamato 75011 | ||||||
| whole rock and density fractions 73 matrix | Rb-Sr | 4.52 | 0.11 | (decay constant 0.0139) | Bansal, Shih, and Wiesmann 1985 | isochron age |
| whole rock and density fractions 73 matrix | Rb-Sr | 4.42 | 0.11 | (decay constant 0.0142) | Bansal, Shih, and Wiesmann 1985 | isochron age |
| whole rock and density fractions 84B clast | Rb-Sr | 4.56 | 0.11 | (decay constant 0.0139) | Bansal, Shih, and Wiesmann 1985 | isochron age |
| whole rock and density fractions 84B clast | Rb-Sr | 4.46 | 0.1 | (decay constant 0.0142) | Bansal, Shih, and Wiesmann 1985 | isochron age |
| 73 matrix, five data points, old decay constant | Rb-Sr | 4.56 | 0.06 | Nyquist et al. 1986 | isochron age | |
| 73 matrix, five data points, new decay constant | Rb-Sr | 4.46 | 0.06 | Nyquist et al. 1986 | isochron age | |
| 73 matrix, nine data points, old decay constant | Rb-Sr | 4.6 | 0.05 | Nyquist et al. 1986 | isochron age | |
| 73 matrix, nine data points, new decay constant | Rb-Sr | 4.5 | 0.05 | Nyquist et al. 1986 | isochron age | |
| five data points | U-Pb | 4.552 | 0.017 | Misawa et al. 2005 | isochron age | |
| 73 matrix, 84B clast, 10 data points | Sm-Nd | 4.55 | 0.14 | Nyquist et al. 1986 | isochron age | |
| 84B clast, seven data points | Sm-Nd | 4.54 | 0.21 | Nyquist et al. 1986 | isochron age | |
Discussion
In contrast to the Allende CV3 carbonaceous chondrite meteorite (Snelling 2014a), there have been fewer radioisotope ages obtained for these eucrites (basaltic achondrites), even though all the radioisotope dating methods have been used on some of them, and a few of the methods on others. Yet the outcome is similar to that found for the ordinary and enstatite chondrites (Snelling 2014b).
Isochron Ages
A 4.55–4.57 Ga isochron age for Bereba, Ibitira, Juvinas, Pasamonte, Serra de Magé, and Yamato 75011 is clearly defined by a strong clustering of their isochron radioisotope data, via the Pb-Pb, U-Pb, Sm-Nd, Rb-Sr, and Lu-Hf methods, though not all these methods cluster for each of these eucrites (fig. 6). As expected, the Mn-Cr, Hf-W, Al-Mg, and I-Xe methods also yield isochron ages that coincide with the Pb-Pb and/or U-Pb isochron ages, simply because the Mn-Cr method is calibrated against the Pb-Pb isochron age of the Lewis Cliff 86010 angrite achondrite (Lugmair and Galer 1992; Lugmair and Shukolyukov 1998), the Hf-W method is calibrated against the Hf-W and Mn-Cr isochron ages of the St. Marguerite H4 chondrite anchored to the weighted average of its U-Pb whole-rock ages (Göpel, Manhès, and Allègre 1994; Kleine et al. 2002, 2004, 2005; Polnau and Lugmair 2001), the Al-Mg method is calibrated against the Pb-Pb isochron age of the CAIs in the CR chondrite Acfer 059 (Amelin et al. 2002; Amelin, Wadhwa and Lugmair 2006; Wadhwa et al. 2004), and the I-Xe method is calibrated against the I-Xe isochron age of the Shallowater aubrite achondrite (Claydon, Crowther, and Gilmour 2013), which is calibrated against the I-Xe isochron and Pb-Pb model ages of phosphate grains from the Acapulco primitive achondrite (Brazzle et al. 1999; Göpel, Manhès, and Allègre 1992, 1994; Nichols et al. 1994).
There is also considerable scattering of the isochron radioisotope age data for these and the other eucrites studied (fig. 6). Many Rb-Sr isochron ages are younger than the 4.55–4.57 Ga clustering (for Bereba, Juvinas, Moore County, Pasamonte, Stannern, and Yamato 75011), though some are older (for Juvinas and Yamato 75011). Similarly many Sm-Nd isochron ages are younger than the 4.55–4.57 Ga clustering (for Bereba, Cacheri, Ibitira, Juvinas, Moama, Moore County, Serra de Magé, and Stannern), while a few are older (for Bereba, Ibitira, and Moore County). Somewhat surprisingly, all the Pb-Pb isochron ages for Bereba, Cacheri, Moama, Moore County, Serra de Magé, and Stannern, and one for Juvinas, are younger than the 4.55–4.57 Ga clustering, much younger in the case of Stannern. In contrast, the U-Pb isochron (concordia) ages are always in or close to that clustering.
No consistent pattern is evident of Rb-Sr and Sm-Nd isochron ages always being younger than the Lu-Hf and U-Th-Pb isochron ages respectively in the order of the parents’ atomic weights or their decay rates (half-lives), according to their β and α decay mode respectively. Such a pattern would be potentially indicative of a past episode of accelerated radioisotope decay, as suggested by Snelling (2005c) and Vardiman, Snelling, and Chaffin (2005) from their radioisotope investigations of earth rocks and minerals.
However, it also has to be taken into account that there is still disagreement over the values of the decay constants and half-lives of, for example, 87Rb and 176Lu (Snelling 2014c, d), because of there being discrepancies between determinations based on comparisons of the Rb-Sr and Lu-Hf ages of meteorites (primarily eucrites), lunar rocks, and earth minerals and rocks with their U-Pb, K-Ar, and Ar-Ar ages. Indeed, the comparisons of ages involving meteorites (primarily eucrites) and lunar rocks yield a slightly higher decay constant and a slightly faster decay rate (half-life) for both 87Rb and 76Lu than for age comparisons involving earth rocks and minerals.
Thus if the different decay constants are used in calculating the Rb-Sr and Lu-Hf ages of eucrites, then the affect would be only small (0.6–4.0%) and would still result in Rb-Sr ages that are apparently too young and Lu-Hf ages that are apparently too old. This would not change the conclusion that there are no systematic isochron age differences based on the different atomic weights of the parent radioisotopes that would be due to a past accelerated decay event. Since in most instances the old decay constants have been used for calculating the isochron Rb-Sr ages but the meteorite decay constant has been used for calculating the isochron Lu-Hf ages, recalculating the isochron Rb-Sr ages using the meteorite decay constant would only bring them closer to agreement with the isochron Lu-Hf ages. This only serves to reinforce the lack of any consistent pattern in the isochron ages obtained by the different radioisotope systems, and thus there is no evidence of a past accelerated decay event.
Model ages
In contrast to the isochron ages for these eucrites (basaltic achondrites), there are many more model ages for them (fig. 7). A 4.55–4.57 Ga model age for Bereba, Cacheri, Camel Donga, Ibitira, and Juvinas is very clearly defined by a strong clustering of Pb-Pb and U-Pb model ages, and for Yamato 75011 supported by Sm-Nd and Rb-Sr model ages. As again expected, the Pu-Xe, Al-Mg, and Mn-Cr model ages always plot in, or closely adjacent to, the strong clustering of Pb-Pb and U-Pb model ages. This is because the Pu-Xe model ages are calibrated against the Pb-Pb isochron age of the Angra dos Reis (ADOR) angrite achondrite (Lugmair and Galer 1992; Lugmair and Marti 1977; Miura et al. 1998; Shukolyukov and Begemann 1996a, b), the Al-Mg model ages are calibrated against the Pb-Pb isochron age of the CAIs in the Allende CV3 chondrite (Jacobsen et al. 2008; Schiller, Baker, and Bizzarro 2010), and the Mn-Cr model age for Caldera is calibrated against its Sm-Nd and Pb-Pb isochron ages (Galer and Lugmair 1996; Wadhwa and Lugmair 1996).
Scattering of the model ages is prolific, with K-Ar and Ar-Ar model ages generally being younger than the 4.55–4.57 Ga clustering for all these eucrite meteorites, except for a few that are older for Ibitira, Moore County, Pasamonte, Serra de Magé, and Stannern (fig. 7). Similarly the U-Pb model ages are either younger or older than the clustering, or in most instances both, whereas for Camel Donga they are usually younger, but for Juvinas and Yamato 75011 they are invariably older. Some of the Pb-Pb model ages for Bereba, Cacheri, Camel Donga, Ibitira, Juvinas, and Stannern are younger than the 4.55–4.57 Ga clustering, sometimes much younger, and a few for Ibitira, Juvinas, and Pasamonte are much older. For Yamato 75011 the Rb-Sr model ages are scattered either side of the strong clustering. Where available for Ibitira and Pasamonte, the Th-Pb model ages are nearly all older.
Table 2. Model ages for whole-rock samples and some or all components of 12 eucrite achondrites, with the details and literature sources.
| Sample | Method | Date | Error +/- | Note | Source | Type |
|---|---|---|---|---|---|---|
| Bereba | ||||||
| whole rock samples | K-Ar | 2.8 | Heymann, Mazor, and Anders 1968 | model age | ||
| pyroxene | K-Ar | 3 | Hampel et al. 1980 | model age | ||
| plagioclase | K-Ar | 3.3 | Hampel et al. 1980 | model age | ||
| K-Ar | 3.31 | Shukolyukov and Begemann 1996b | model age | |||
| whole rock | Pb-Pb | 4.44 | Manhès et al. 1975 | model age | ||
| whole rock sample | Pb-Pb | 4.44 | Manhès et al. 1975 | model age | ||
| Pb-Pb | 4.415 | Manhès et al. 1975 | model age | |||
| whole rock samples | Pb-Pb | 4.536 | Carlson Tera, and Boctor 1988 | model age | ||
| whole rock, single stage model | Pb-Pb | 4.536 | Tera, Carlson, and Boctor 1997 | model age | ||
| mean of all Pb isotope combinations on all samples | Pb-Pb | 4.521 | 0.0004 | Tera, Carlson, and Boctor 1997 | model age | |
| zircons | 207Pb-206Pb | 4.534 | 0.016 | Bukovanska and Ireland 1993 | model age | |
| weighted average of five analyses of three zircon grains | 207Pb-206Pb | 4.552 | 0.02 | Zhou et al. 2013 | model age | |
| Spot 1-1 | 207Pb-206Pb | 4.515 | 0.025 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 207Pb-206Pb | 4.569 | 0.02 | Zhou et al. 2013 | model age | |
| Spot 2 | 207Pb-206Pb | 4.574 | 0.026 | Zhou et al. 2013 | model age | |
| Spot 3-1 | 207Pb-206Pb | 4.549 | 0.019 | Zhou et al. 2013 | model age | |
| Spot 3-2 | 207Pb-206Pb | 4.545 | 0.024 | Zhou et al. 2013 | model age | |
| Spot 1-1 | 207Pb-235U | 4.425 | 0.034 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 207Pb-235U | 4.572 | 0.03 | Zhou et al. 2013 | model age | |
| Spot 2 | 207Pb-235U | 4.563 | 0.032 | Zhou et al. 2013 | model age | |
| Spot 3-1 | 207Pb-235U | 4.637 | 0.037 | Zhou et al. 2013 | model age | |
| Spot 3-2 | 207Pb-235U | 4.49 | 0.031 | Zhou et al. 2013 | model age | |
| Spot 1-1 | 206Pb-238U | 4.229 | 0.089 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 206Pb-238U | 4.579 | 0.085 | Zhou et al. 2013 | model age | |
| Spot 2 | 206Pb-238U | 4.539 | 0.084 | Zhou et al. 2013 | model age | |
| Spot 3-1 | 206Pb-238U | 4.841 | 0.114 | Zhou et al. 2013 | model age | |
| Spot 3-2 | 206Pb-238U | 4.369 | 0.083 | Zhou et al. 2013 | model age | |
| Pu-Xe | 4.498 | 0.016 | Shukolyukov and Begemann 1996a | model age | ||
| whole rock sample relative to ADOR | Pu-Xe | 4.512 | 0.018 | Miura et al. 1998 | model age | |
| Cachari | ||||||
| whole rock sample | Ar-Ar | 3.04 | 0.7 | Bogard et al. 1985 | model age | |
| whole rock sample | Ar-Ar | 3.47 | 0.4 | Bogard et al. 1985 | model age | |
| whole rock sample | Pb-Pb | 4.13 | Tera, Carlson, and Boctor 1987 | model age | ||
| three analyses of one zircon grain | 207Pb-206Pb | 4.549 | 0.013 | weighted average | Zhou et al. 2011 | model age |
| sixteen analyses of six zircon grains | 207Pb-206Pb | 4.551 | 0.014 | weighted mean | Zhou et al. 2013 | model age |
| Grain 1-1 | 207Pb-206Pb | 4.539 | 0.017 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 1-2 | 207Pb-206Pb | 4.533 | 0.017 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 1-3 | 207Pb-206Pb | 4.556 | 0.017 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 2-1 | 207Pb-206Pb | 4.535 | 0.019 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 3-1 | 207Pb-206Pb | 4.579 | 0.016 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 3-2 | 207Pb-206Pb | 4.587 | 0.016 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 3-3 | 207Pb-206Pb | 4.596 | 0.016 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 4-1 | 207Pb-206Pb | 4.565 | 0.019 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 4-2 | 207Pb-206Pb | 4.546 | 0.021 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 5-1 | 207Pb-206Pb | 4.51 | 0.019 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 5-2 | 207Pb-206Pb | 4.516 | 0.019 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 5-3 | 207Pb-206Pb | 4.524 | 0.018 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 5-4 | 207Pb-206Pb | 4.563 | 0.018 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 5-5 | 207Pb-206Pb | 4.54 | 0.019 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 6-1 | 207Pb-206Pb | 4.558 | 0.019 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 6-2 | 207Pb-206Pb | 4.515 | 0.019 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 6-3 | 207Pb-206Pb | 4.564 | 0.02 | ages using Canyon Diablo troilite Pb | Zhou et al. 2013 | model age |
| Grain 1-1 | 207Pb-206Pb | 4.539 | 0.018 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 1-2 | 207Pb-206Pb | 4.533 | 0.018 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 1-3 | 207Pb-206Pb | 4.557 | 0.016 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 2-1 | 207Pb-206Pb | 4.536 | 0.019 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 3-1 | 207Pb-206Pb | 4.58 | 0.016 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 3-2 | 207Pb-206Pb | 4.588 | 0.016 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 3-3 | 207Pb-206Pb | 4.596 | 0.016 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 4-1 | 207Pb-206Pb | 4.566 | 0.019 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 4-2 | 207Pb-206Pb | 4.547 | 0.021 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 5-1 | 207Pb-206Pb | 4.51 | 0.019 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 5-2 | 207Pb-206Pb | 4.516 | 0.019 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 5-3 | 207Pb-206Pb | 4.524 | 0.018 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 5-4 | 207Pb-206Pb | 4.563 | 0.018 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 5-5 | 207Pb-206Pb | 4.54 | 0.019 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 6-1 | 207Pb-206Pb | 4.559 | 0.019 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 6-2 | 207Pb-206Pb | 4.515 | 0.017 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| Grain 6-3 | 207Pb-206Pb | 4.565 | 0.02 | ages using terrestrial common Pb | Zhou et al. 2013 | model age |
| weighted averages of three analyses of one zircon grain | 207Pb-206Pb | 4.55 | 0.039 | Zhou et al. 2013 | model age | |
| Spot 7-1 | 207Pb-206Pb | 4.529 | 0.013 | Zhou et al. 2013 | model age | |
| Spot 7-2 | 207Pb-206Pb | 4.549 | 0.032 | Zhou et al. 2013 | model age | |
| Spot 7-3 | 207Pb-206Pb | 4.596 | 0.093 | Zhou et al. 2013 | model age | |
| weighted averages of three analyses of one zircon grain | 207Pb-235U | 4.568 | 0.033 | Zhou et al. 2013 | model age | |
| Spot 7-1 | 207Pb-235U | 4.561 | 0.013 | Zhou et al. 2013 | model age | |
| Spot 7-2 | 207Pb-235U | 4.562 | 0.029 | Zhou et al. 2013 | model age | |
| Spot 7-3 | 207Pb-235U | 4.565 | 0.081 | Zhou et al. 2013 | model age | |
| weighted averages of three analyses of one zircon grain | 206Pb-238U | 4.608 | 0.096 | Zhou et al. 2013 | model age | |
| Spot 7-1 | 206Pb-238U | 4.555 | 0.01 | Zhou et al. 2013 | model age | |
| Spot 7-2 | 206Pb-238U | 4.586 | 0.027 | Zhou et al. 2013 | model age | |
| Spot 7-3 | 206Pb-238U | 4.659 | 0.081 | Zhou et al. 2013 | model age | |
| whole rock sample relative to ADOR | Pu-Xe | 4.498 | Shukolyukov and Begemann 1996a | model age | ||
| glass sample relative to ADOR | Pu-Xe | 4.517 | Shukolyukov and Begemann 1996b | model age | ||
| Caldera | ||||||
| whole rock sample | K-Ar | 4.19 | Shukolyukov and Begemann 1996b | model age | ||
| pyroxene fraction | Pb-Pb | 4.525 | 0.0019 | Galer and Lugmair 1996 | model age | |
| weighted mean of four points on one zircon grain | Pb-Pb | 4.542 | 0.08 | Zhou et al. 2013 | model age | |
| Spot 1-1 | 207Pb-206Pb | 4.591 | 0.034 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 207Pb-206Pb | 4.502 | 0.045 | Zhou et al. 2013 | model age | |
| Spot 1-3 | 207Pb-206Pb | 4.49 | 0.03 | Zhou et al. 2013 | model age | |
| Spot 1-4 | 207Pb-206Pb | 4.573 | 0.029 | Zhou et al. 2013 | model age | |
| Spot 1-1 | 207Pb-235U | 4.575 | 0.069 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 207Pb-235U | 4.491 | 0.074 | Zhou et al. 2013 | model age | |
| Spot 1-3 | 206Pb-238U | 5.131 | 0.156 | Zhou et al. 2013 | model age | |
| Spot 1-4 | 206Pb-238U | 5.048 | 0.133 | Zhou et al. 2013 | model age | |
| Spot 1-1 | 206Pb-238U | 4.54 | 0.204 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 206Pb-238U | 4.467 | 0.207 | Zhou et al. 2013 | model age | |
| Spot 1-3 | 207Pb-235U | 4.68 | 0.05 | Zhou et al. 2013 | model age | |
| Spot 1-4 | 207Pb-235U | 4.714 | 0.044 | Zhou et al. 2013 | model age | |
| anchored to other meteorite dates | Mn-Cr | 4.537 | 0.012 | Wadhwa and Lugmair 1996 | model age | |
| Pu-Xe | 4.513 | Shukolyukov and Begemann 1996a | model age | |||
| Camel Donga | ||||||
| matrix samples with pyroxenes, weighted | Ar-Ar | 3.704 | 0.079 | Kennedy et al. 2013 | plateau age | |
| matrix samples with pyroxenes, weighted | Ar-Ar | 3.67 | 0.08 | Kennedy et al. 2013 | plateau age | |
| weight mean of two | Ar-Ar | 3.693 | 0.051 | Kennedy et al. 2013 | plateau age | |
| pyroxene fraction | Pb-Pb | 4.5109 | 0.001 | Iizuka et al. 2013 | model age | |
| thirty-five point analyses of 14 zircon grains | 207Pb-206Pb | 4.531 | 0.01 | weighted average | Zhou et al. 2013 | model age |
| Spot 1-1 | 207Pb-206Pb | 4.525 | 0.014 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 207Pb-206Pb | 4.579 | 0.012 | Zhou et al. 2013 | model age | |
| Spot 2-1 | 207Pb-206Pb | 4.551 | 0.023 | Zhou et al. 2013 | model age | |
| Spot 2-2 | 207Pb-206Pb | 4.547 | 0.017 | Zhou et al. 2013 | model age | |
| Spot 3 | 207Pb-206Pb | 4.552 | 0.051 | Zhou et al. 2013 | model age | |
| Spot 4 | 207Pb-206Pb | 4.512 | 0.02 | Zhou et al. 2013 | model age | |
| Spot 5-1 | 207Pb-206Pb | 4.572 | 0.033 | Zhou et al. 2013 | model age | |
| Spot 5-2 | 207Pb-206Pb | 4.516 | 0.032 | Zhou et al. 2013 | model age | |
| Spot 5-3 | 207Pb-206Pb | 4.531 | 0.02 | Zhou et al. 2013 | model age | |
| Spot 6 | 207Pb-206Pb | 4.479 | 0.034 | Zhou et al. 2013 | model age | |
| Spot 7-1 | 207Pb-206Pb | 4.546 | 0.014 | Zhou et al. 2013 | model age | |
| Spot 7-2 | 207Pb-206Pb | 4.517 | 0.02 | Zhou et al.. 2013 | model age | |
| Spot 7-3 | 207Pb-206Pb | 4.557 | 0.013 | Zhou et al. 2013 | model age | |
| Spot 7-4 | 207Pb-206Pb | 4.53 | 0.021 | Zhou et al. 2013 | model age | |
| Spot 8 | 207Pb-206Pb | 4.484 | 0.022 | Zhou et al. 2013 | model age | |
| Spot 9-1 | 207Pb-206Pb | 4.546 | 0.019 | Zhou et al. 2013 | model age | |
| Spot 9-2 | 207Pb-206Pb | 4.542 | 0.023 | Zhou et al. 2013 | model age | |
| Spot 9-3 | 207Pb-206Pb | 4.536 | 0.018 | Zhou et al. 2013 | model age | |
| Spot 9-4 | 207Pb-206Pb | 4.471 | 0.03 | Zhou et al. 2013 | model age | |
| Spot 9-5 | 207Pb-206Pb | 4.507 | 0.032 | Zhou et al. 2013 | model age | |
| Spot 9-6 | 207Pb-206Pb | 4.514 | 0.025 | Zhou et al. 2013 | model age | |
| Spot 9-7 | 207Pb-206Pb | 4.535 | 0.037 | Zhou et al. 2013 | model age | |
| Spot 10-1 | 207Pb-206Pb | 4.519 | 0.022 | Zhou et al. 2013 | model age | |
| Spot 10-2 | 207Pb-206Pb | 4.481 | 0.022 | Zhou et al. 2013 | model age | |
| Spot 10-3 | 207Pb-206Pb | 4.525 | 0.019 | Zhou et al. 2013 | model age | |
| Spot 11 | 207Pb-206Pb | 4.534 | 0.046 | Zhou et al. 2013 | model age | |
| Spot 12-1 | 207Pb-206Pb | 4.566 | 0.019 | Zhou et al. 2013 | model age | |
| Spot 12-2 | 207Pb-206Pb | 4.537 | 0.017 | Zhou et al. 2013 | model age | |
| Spot 12-3 | 207Pb-206Pb | 4.536 | 0.018 | Zhou et al. 2013 | model age | |
| Spot 12-4 | 207Pb-206Pb | 4.57 | 0.015 | Zhou et al. 2013 | model age | |
| Spot 12-5 | 207Pb-206Pb | 4.551 | 0.026 | Zhou et al. 2013 | model age | |
| Spot 13 | 207Pb-206Pb | 4.511 | 0.022 | Zhou et al. 2013 | model age | |
| Spot 14-1 | 207Pb-206Pb | 4.478 | 0.013 | Zhou et al. 2013 | model age | |
| Spot 14-2 | 207Pb-206Pb | 4.479 | 0.016 | Zhou et al. 2013 | model age | |
| Spot 14-3 | 207Pb-206Pb | 4.52 | 0.014 | Zhou et al. 2013 | model age | |
| thirty-five point analyses of 14 zircon grains | 207Pb-235U | 4.492 | 0.023 | weighted average | Zhou et al. 2013 | model age |
| Spot 1-1 | 207Pb-235U | 4.461 | 0.034 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 207Pb-235U | 4.419 | 0.033 | Zhou et al. 2013 | model age | |
| Spot 2-1 | 207Pb-235U | 4.466 | 0.042 | Zhou et al. 2013 | model age | |
| Spot 2-2 | 207Pb-235U | 4.513 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 3 | 207Pb-235U | 4.561 | 0.064 | Zhou et al. 2013 | model age | |
| Spot 4 | 207Pb-235U | 4.405 | 0.036 | Zhou et al. 2013 | model age | |
| Spot 5-1 | 207Pb-235U | 4.531 | 0.043 | Zhou et al. 2013 | model age | |
| Spot 5-2 | 207Pb-235U | 4.48 | 0.042 | Zhou et al. 2013 | model age | |
| Spot 5-3 | 207Pb-235U | 4.493 | 0.036 | Zhou et al. 2013 | model age | |
| Spot 6 | 207Pb-235U | 4.691 | 0.042 | Zhou et al. 2013 | model age | |
| Spot 7-1 | 207Pb-235U | 4.469 | 0.034 | Zhou et al. 2013 | model age | |
| Spot 7-2 | 207Pb-235U | 4.486 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 7-3 | 207Pb-235U | 4.433 | 0.034 | Zhou et al. 2013 | model age | |
| Spot 7-4 | 207Pb-235U | 4.513 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 8 | 207Pb-235U | 4.597 | 0.037 | Zhou et al. 2013 | model age | |
| Spot 9-1 | 207Pb-235U | 4.53 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 9-2 | 207Pb-235U | 4.657 | 0.037 | Zhou et al. 2013 | model age | |
| Spot 9-3 | 207Pb-235U | 4.451 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 9-4 | 207Pb-235U | 4.586 | 0.038 | Zhou et al. 2013 | model age | |
| Spot 9-5 | 207Pb-235U | 4.374 | 0.041 | Zhou et al. 2013 | model age | |
| Spot 9-6 | 207Pb-235U | 4.545 | 0.039 | Zhou et al. 2013 | model age | |
| Spot 9-7 | 207Pb-235U | 4.498 | 0.045 | Zhou et al. 2013 | model age | |
| Spot 10-1 | 207Pb-235U | 4.539 | 0.036 | Zhou et al. 2013 | model age | |
| Spot 10-2 | 207Pb-235U | 4.451 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 10-3 | 207Pb-235U | 4.497 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 11 | 207Pb-235U | 4.52 | 0.05 | Zhou et al. 2013 | model age | |
| Spot 12-1 | 207Pb-235U | 4.473 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 12-2 | 207Pb-235U | 4.476 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 12-3 | 207Pb-235U | 4.431 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 12-4 | 207Pb-235U | 4.496 | 0.035 | Zhou et al. 2013 | model age | |
| Spot 12-5 | 207Pb-235U | 4.568 | 0.039 | Zhou et al. 2013 | model age | |
| Spot 13 | 207Pb-235U | 4.523 | 0.036 | Zhou et al. 2013 | model age | |
| Spot 14-1 | 207Pb-235U | 4.437 | 0.033 | Zhou et al. 2013 | model age | |
| Spot 14-2 | 207Pb-235U | 4.405 | 0.034 | Zhou et al. 2013 | model age | |
| Spot 14-3 | 207Pb-235U | 4.447 | 0.034 | Zhou et al. 2013 | model age | |
| thirty-five point analyses of 14 zircon grains | 206Pb-238U | 4.417 | 0.079 | weighted average | Zhou et al. 2013 | model age |
| Spot 1-1 | 206Pb-238U | 4.32 | 0.101 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 206Pb-238U | 4.077 | 0.096 | Zhou et al. 2013 | model age | |
| Spot 2-1 | 206Pb-238U | 4.279 | 0.12 | Zhou et al. 2013 | model age | |
| Spot 2-2 | 206Pb-238U | 4.438 | 0.104 | Zhou et al. 2013 | model age | |
| Spot 3 | 206Pb-238U | 4.582 | 0.167 | Zhou et al. 2013 | model age | |
| Spot 4 | 206Pb-238U | 4.174 | 0.101 | Zhou et al. 2013 | model age | |
| Spot 5-1 | 206Pb-238U | 4.439 | 0.112 | Zhou et al. 2013 | model age | |
| Spot 5-2 | 206Pb-238U | 4.4 | 0.111 | Zhou et al. 2013 | model age | |
| Spot 5-3 | 206Pb-238U | 4.41 | 0.104 | Zhou et al. 2013 | model age | |
| Spot 6 | 206Pb-238U | 5.196 | 0.119 | Zhou et al. 2013 | model age | |
| Spot 7-1 | 206Pb-238U | 4.301 | 0.101 | Zhou et al. 2013 | model age | |
| Spot 7-2 | 206Pb-238U | 4.417 | 0.1 | Zhou et al. 2013 | model age | |
| Spot 7-3 | 206Pb-238U | 4.165 | 0.1 | Zhou et al. 2013 | model age | |
| Spot 7-4 | 206Pb-238U | 4.476 | 0.101 | Zhou et al. 2013 | model age | |
| Spot 8 | 206Pb-238U | 4.857 | 0.112 | Zhou et al. 2013 | model age | |
| Spot 9-1 | 206Pb-238U | 4.495 | 0.105 | Zhou et al. 2013 | model age | |
| Spot 9-2 | 206Pb-238U | 4.923 | 0.114 | Zhou et al. 2013 | model age | |
| Spot 9-3 | 206Pb-238U | 4.267 | 0.101 | Zhou et al. 2013 | model age | |
| Spot 9-4 | 206Pb-238U | 4.852 | 0.108 | Zhou et al. 2013 | model age | |
| Spot 9-5 | 206Pb-238U | 4.091 | 0.102 | Zhou et al. 2013 | model age | |
| Spot 9-6 | 206Pb-238U | 4.616 | 0.112 | Zhou et al. 2013 | model age | |
| Spot 9-7 | 206Pb-238U | 4.415 | 0.115 | Zhou et al. 2013 | model age | |
| Spot 10-1 | 206Pb-238U | 4.584 | 0.105 | Zhou et al. 2013 | model age | |
| Spot 10-2 | 206Pb-238U | 4.385 | 0.1 | Zhou et al. 2013 | model age | |
| Spot 10-3 | 206Pb-238U | 4.435 | 0.103 | Zhou et al. 2013 | model age | |
| Spot 11 | 206Pb-238U | 4.489 | 0.118 | Zhou et al. 2013 | model age | |
| Spot 12-1 | 206Pb-238U | 4.271 | 0.099 | Zhou et al. 2013 | model age | |
| Spot 12-2 | 206Pb-238U | 4.343 | 0.103 | Zhou et al. 2013 | model age | |
| Spot 12-3 | 206Pb-238U | 4.206 | 0.101 | Zhou et al. 2013 | model age | |
| Spot 12-4 | 206Pb-238U | 4.334 | 0.103 | Zhou et al. 2013 | model age | |
| Spot 12-5 | 206Pb-238U | 4.607 | 0.11 | Zhou et al. 2013 | model age | |
| Spot 13 | 206Pb-238U | 4.549 | 0.106 | Zhou et al. 2013 | model age | |
| Spot 14-1 | 206Pb-238U | 4.346 | 0.1 | Zhou et al. 2013 | model age | |
| Spot 14-2 | 206Pb-238U | 4.246 | 0.1 | Zhou et al. 2013 | model age | |
| Spot 14-3 | 206Pb-238U | 4.288 | 0.1 | Zhou et al. 2013 | model age | |
| Al-Mg | 4.5647 | 0.0004 | Schiller, Baker, and Bizzarro 2010 | model age | ||
| relative to ADOR | Pu-Xe | 4.521 | 0.02 | Shukolyukov and Begemann 1996a | model age | |
| average of seven samples relative to ADOR | Pu-Xe | 4.507 | 0.016 | Miura et al. 1998 | model age | |
| Ibitira | ||||||
| whole-rock samples | K-Ar | 3.2 | Heymann, Mazor, and Anders 1968 | model age | ||
| Ar-Ar | 4.49 | Garrison and Bogard 1995 | model age | |||
| using 15 stepwise temperature extractions | Ar-Ar | 4.495 | 0.015 | Bogard and Garrison 1995 | plateau age | |
| Sample at 400°C | Ar-Ar | 3.354 | 0.048 | Bogard and Garrison 1995 | extraction age | |
| Sample at 500°C | Ar-Ar | 3.205 | 0.051 | Bogard and Garrison 1995 | extraction age | |
| Sample at 600°C | Ar-Ar | 3.525 | 0.023 | Bogard and Garrison 1995 | extraction age | |
| Sample at 700°C | Ar-Ar | 3.874 | 0.008 | Bogard and Garrison 1995 | extraction age | |
| Sample at 775°C | Ar-Ar | 4.361 | 0.009 | Bogard and Garrison 1995 | extraction age | |
| Sample at 825°C | Ar-Ar | 4.469 | 0.01 | Bogard and Garrison 1995 | extraction age | |
| Sample at 875°C | Ar-Ar | 4.502 | 0.009 | Bogard and Garrison 1995 | extraction age | |
| Sample at 930°C | Ar-Ar | 4.493 | 0.009 | Bogard and Garrison 1995 | extraction age | |
| Sample at 975°C | Ar-Ar | 4.491 | 0.009 | Bogard and Garrison 1995 | extraction age | |
| Sample at 1025°C | Ar-Ar | 4.509 | 0.008 | Bogard and Garrison 1995 | extraction age | |
| Sample at 1100°C | Ar-Ar | 4.452 | 0.029 | Bogard and Garrison 1995 | extraction age | |
| Sample at 1200°C | Ar-Ar | 4.491 | 0.098 | Bogard and Garrison 1995 | extraction age | |
| Sample at 1300°C | Ar-Ar | 4.588 | 0.036 | Bogard and Garrison 1995 | extraction age | |
| Sample at 1400°C | Ar-Ar | 4.48 | 0.103 | Bogard and Garrison 1995 | extraction age | |
| Sample at 1550°C | Ar-Ar | 7.998 | 0.425 | Bogard and Garrison 1995 | extraction age | |
| after Bogard and Garrison (1995) | Ar-Ar | 4.487 | 0.015 | Yamaguchi et al. 2001 | plateau (model) age | |
| five extractions releasing 89% of Ar | Ar-Ar | 4.487 | 0.016 | Bogard and Garrison 2003 | plateau age | |
| after Bogard and Garrison (1995) | Ar-Ar | 4.4858 | 0.015 | Claydon, Crowther, and Gilmour 2012 | plateau (model) age | |
| 207Pb-206Pb | 4.55 | 0.01 | Wasserburg et al. 1977 | model age | ||
| Ibitira WR-1 | 207Pb-206Pb | 4.554 | 0.008 | Chen and Wasserburg 1985 | model age | |
| Ibitira WR-2 | 207Pb-206Pb | 4.556 | 0.006 | Chen and Wasserburg 1985 | model age | |
| 207Pb-206Pb | 4.56 | 0.003 | Manhès, Göpel, and Allègre 1987 | model age | ||
| pyroxene fraction | Pb-Pb | 4.5558 | 0.0005 | Iizuka et al. 2013 | model age | |
| whole rock fraction A017_7 residue | Pb-Pb | 4.5564 | 0.0011 | Iizuka et al. 2014 | model age | |
| whole rock fraction A017_7 wash-1 | Pb-Pb | 4.5543 | 0.0022 | Iizuka et al. 2014 | model age | |
| whole rock fraction A017_7 wash-2 | Pb-Pb | 4.584 | 0.0022 | Iizuka et al. 2014 | model age | |
| whole rock fraction A039_5 residue | Pb-Pb | 4.556 | 0.0008 | Iizuka et al. 2014 | model age | |
| whole rock fraction A039_5 wash-1 | Pb-Pb | 4.5894 | 0.0022 | Iizuka et al. 2014 | model age | |
| whole rock fraction A039_5 wash-2 | Pb-Pb | 4.5881 | 0.0036 | Iizuka et al. 2014 | model age | |
| whole rock fraction A047_3 residue | Pb-Pb | 4.5572 | 0.0013 | Iizuka et al. 2014 | model age | |
| whole rock fraction A047_3 wash-1 | Pb-Pb | 4.608 | 0.0024 | Iizuka et al. 2014 | model age | |
| whole rock fraction A047_3 wash-2 | Pb-Pb | 4.6043 | 0.0054 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction GSC030_HF1 residue | Pb-Pb | 4.5558 | 0.0007 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction GSC030_HF1 wash-1 | Pb-Pb | 4.5533 | 0.0002 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction GSC030_HF1 wash-2 | Pb-Pb | 4.556 | 0.0021 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction GSC030_HF2 residue | Pb-Pb | 4.5559 | 0.0007 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction GSC030_HF2 wash-1 | Pb-Pb | 4.553 | 0.0002 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction GSC030_HF2 wash-2 | Pb-Pb | 4.558 | 0.0024 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A015_4 residue | Pb-Pb | 4.5558 | 0.0009 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A015_4 wash-1 | Pb-Pb | 4.5361 | 0.002 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A015_4 wash-2 | Pb-Pb | 4.6139 | 0.0549 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A015_5 residue | Pb-Pb | 4.5506 | 0.0075 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A015_5 wash-1 | Pb-Pb | 4.5141 | 0.0021 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A015_5 wash-2 | Pb-Pb | 4.5709 | 0.0201 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A015_6 residue | Pb-Pb | 4.552 | 0.001 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A015_6 wash-1 | Pb-Pb | 4.5211 | 0.001 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A015_6 wash-2 | Pb-Pb | 4.5329 | 0.0242 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A017_5 residue | Pb-Pb | 4.5581 | 0.0013 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A017_5 wash-2 | Pb-Pb | 4.5727 | 0.0025 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A017_6 residue | Pb-Pb | 4.5546 | 0.0009 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A017_6 wash-1 | Pb-Pb | 4.552 | 0.001 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A017_6 wash-2 | Pb-Pb | 4.5265 | 0.0065 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A039_2 residue | Pb-Pb | 4.5563 | 0.0007 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A039_2 wash-1 | Pb-Pb | 4.5634 | 0.0016 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A039_2 wash-2 | Pb-Pb | 4.539 | 0.0038 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A039_3 residue | Pb-Pb | 4.5562 | 0.0008 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A039_3 wash-1 | Pb-Pb | 4.5822 | 0.0024 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A039_3 wash-2 | Pb-Pb | 4.5594 | 0.0045 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A047_1 residue | Pb-Pb | 4.5565 | 0.0006 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A047_1 wash-1 | Pb-Pb | 4.5583 | 0.0014 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A047_1 wash-2 | Pb-Pb | 4.5815 | 0.0125 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A047_2 residue | Pb-Pb | 4.5567 | 0.0007 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A047_2 wash-1 | Pb-Pb | 4.5632 | 0.002 | Iizuka et al. 2014 | model age | |
| pyroxene-rich fraction A047_2 wash-2 | Pb-Pb | 4.5843 | 0.0159 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A015_7 residue | Pb-Pb | 4.5381 | 0.0052 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A015_7 wash-1 | Pb-Pb | 4.5232 | 0.001 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A015_7 wash-2 | Pb-Pb | 4.6072 | 0.0072 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A015_8 residue | Pb-Pb | 4.5139 | 0.0038 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A015_8 wash-1 | Pb-Pb | 4.5456 | 0.0008 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A015_8 wash-2 | Pb-Pb | 4.6352 | 0.0032 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A039_4 residue | Pb-Pb | 4.5636 | 0.0135 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A039_4 wash-1 | Pb-Pb | 4.5515 | 0.0007 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A039_4 wash-2 | Pb-Pb | 4.6311 | 0.0058 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A047_4 residue | Pb-Pb | 4.5595 | 0.0108 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A047_4 wash-1 | Pb-Pb | 4.5606 | 0.0006 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A047_4 wash-2 | Pb-Pb | 4.6722 | 0.0123 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A047_5 residue | Pb-Pb | 4.5528 | 0.0019 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A047_5 wash-1 | Pb-Pb | 4.5572 | 0.0005 | Iizuka et al. 2014 | model age | |
| plagioclase-rich fraction A047_5 wash-2 | Pb-Pb | 4.387 | 0.0275 | Iizuka et al. 2014 | model age | |
| weighted average of residues of 8 pyroxene-rich fractions and two whole-rock fractions and washes of two pyroxene-rich and one plagioclase-rich fractions (13 ages) | Pb-Pb | 4.55635 | 0.00042 | Iizuka et al. 2014 | model age | |
| weighted average of residues of one whole-rock and six pyroxene-rich fractions (seven ages) | Pb-Pb | 4.55631 | 0.00028 | Iizuka et al. 2014 | model age | |
| Ibitira WR-1 | 206Pb-238U | 4.629 | 0.03 | Chen and Wasserburg 1985 | model age | |
| Ibitira WR-2 | 206Pb-238U | 4.567 | 0.013 | Chen and Wasserburg 1985 | model age | |
| Ibitira WR-1 | 207Pb-235U | 4.577 | 0.007 | Chen and Wasserburg 1985 | model age | |
| Ibitira WR-2 | 207Pb-235U | 4.559 | 0.005 | Chen and Wasserburg 1985 | model age | |
| Ibitira WR-1 | 208Pb-232Th | 4.972 | 0.036 | Chen and Wasserburg 1985 | model age | |
| Ibitira WR-2 | 208Pb-232Th | 4.658 | 0.022 | Chen and Wasserburg 1985 | model age | |
| Single sample | Pu-Xe | 4.581 | 0.025 | Shukolyukov and Begemann 1996a | model age | |
| Juvinas | ||||||
| whole rock samples | K-Ar | 3.98 | Heymann, Mazor, and Anders 1968 | model age | ||
| plagioclase sample | K-Ar | 4.6 | Hampel et al. 1980 | model age | ||
| frB58 | Pb-Pb | 4.5676 | 0.0011 | Manhès, Allègre, and Provost 1984 | model age | |
| frB60 | Pb-Pb | 4.5676 | 0.0034 | Manhès, Allègre, and Provost 1984 | model age | |
| frB63 | Pb-Pb | 4.5648 | 0.001 | Manhès, Allègre, and Provost 1984 | model age | |
| frC64 | Pb-Pb | 4.5646 | 0.0011 | Manhès, Allègre, and Provost 1984 | model age | |
| frC65 | Pb-Pb | 4.5656 | 0.0008 | Manhès, Allègre, and Provost 1984 | model age | |
| frC66 | Pb-Pb | 4.5658 | 0.0007 | Manhès, Allègre, and Provost 1984 | model age | |
| frC67 | Pb-Pb | 4.5649 | 0.001 | Manhès, Allègre, and Provost 1984 | model age | |
| frD70 | Pb-Pb | 4.5534 | 0.0006 | Manhès, Allègre, and Provost 1984 | model age | |
| pla54 | Pb-Pb | 4.796 | 0.0075 | Manhès, Allègre, and Provost 1984 | model age | |
| pla57 | Pb-Pb | 4.7278 | 0.0049 | Manhès, Allègre, and Provost 1984 | model age | |
| pla62 | Pb-Pb | 4.821 | 0.0011 | Manhès, Allègre, and Provost 1984 | model age | |
| pla70 | Pb-Pb | 4.7979 | 0.0044 | Manhès, Allègre, and Provost 1984 | model age | |
| pyr62 | Pb-Pb | 4.5726 | 0.0038 | Manhès, Allègre, and Provost 1984 | model age | |
| pyr70 | Pb-Pb | 4.5768 | 0.0017 | Manhès, Allègre, and Provost 1984 | model age | |
| L1 | Pb-Pb | 4.634 | 0.003 | Manhès, Allègre, and Provost 1984 | model age | |
| L2 | Pb-Pb | 4.8131 | 0.0097 | Manhès, Allègre, and Provost 1984 | model age | |
| L3 | Pb-Pb | 4.8 | 0.0011 | Manhès, Allègre, and Provost 1984 | model age | |
| Res | Pb-Pb | 4.953 | 0.0015 | Manhès, Allègre, and Provost 1984 | model age | |
| plaC | Pb-Pb | 4.735 | Manhès, Allègre, and Provost 1984 | model age | ||
| average age | Pb-Pb | 4.527 | 0.024 | two zircons | Lee et al. 2009 | model age |
| 207Pb-206Pb | 4.549 | 0.006 | clast sample | Manhès and Allègre 1980 | model age | |
| weighted average of 20 model ages determined on seven zircon grains | 207Pb-206Pb | 4.545 | 0.015 | Zhou et al. 2013 | model age | |
| Spot 1-1 | 207Pb-206Pb | 4.54 | 0.024 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 207Pb-206Pb | 4.493 | 0.022 | Zhou et al. 2013 | model age | |
| Spot 1-3 | 207Pb-206Pb | 4.502 | 0.024 | Zhou et al. 2013 | model age | |
| Spot 1-4 | 207Pb-206Pb | 4.54 | 0.024 | Zhou et al. 2013 | model age | |
| Spot 1-5 | 207Pb-206Pb | 4.568 | 0.025 | Zhou et al. 2013 | model age | |
| Spot 1-6 | 207Pb-206Pb | 4.52 | 0.024 | Zhou et al. 2013 | model age | |
| Spot 1-7 | 207Pb-206Pb | 4.545 | 0.024 | Zhou et al. 2013 | model age | |
| Spot 2-1 | 207Pb-206Pb | 4.557 | 0.025 | Zhou et al. 2013 | model age | |
| Spot 2-2 | 207Pb-206Pb | 4.497 | 0.024 | Zhou et al. 2013 | model age | |
| Spot 3-1 | 207Pb-206Pb | 4.563 | 0.016 | Zhou et al. 2013 | model age | |
| Spot 3-2 | 207Pb-206Pb | 4.571 | 0.01 | Zhou et al. 2013 | model age | |
| Spot 3-3 | 207Pb-206Pb | 4.559 | 0.011 | Zhou et al. 2013 | model age | |
| Spot 4-1 | 207Pb-206Pb | 4.525 | 0.027 | Zhou et al. 2013 | model age | |
| Spot 4-2 | 207Pb-206Pb | 4.576 | 0.015 | Zhou et al. 2013 | model age | |
| Spot 4-3 | 207Pb-206Pb | 4.584 | 0.02 | Zhou et al. 2013 | model age | |
| Spot 4-4 | 207Pb-206Pb | 4.523 | 0.021 | Zhou et al. 2013 | model age | |
| Spot 5-1 | 207Pb-206Pb | 4.486 | 0.022 | Zhou et al. 2013 | model age | |
| Spot 5-2 | 207Pb-206Pb | 4.511 | 0.019 | Zhou et al. 2013 | model age | |
| Spot 6 | 207Pb-206Pb | 4.472 | 0.026 | Zhou et al. 2013 | model age | |
| Spot 7 | 207Pb-206Pb | 4.516 | 0.041 | Zhou et al. 2013 | model age | |
| weighted average of 20 model ages determined on seven zircon grains | 207Pb-235U | 4.679 | 0.048 | Zhou et al. 2013 | model age | |
| Spot 1-1 | 207Pb-235U | 4.581 | 0.036 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 207Pb-235U | 4.508 | 0.043 | Zhou et al. 2013 | model age | |
| Spot 1-3 | 207Pb-235U | 4.546 | 0.038 | Zhou et al. 2013 | model age | |
| Spot 1-4 | 207Pb-235U | 4.654 | 0.043 | Zhou et al. 2013 | model age | |
| Spot 1-5 | 207Pb-235U | 4.613 | 0.052 | Zhou et al. 2013 | model age | |
| Spot 1-6 | 207Pb-235U | 4.683 | 0.04 | Zhou et al. 2013 | model age | |
| Spot 1-7 | 207Pb-235U | 4.703 | 0.048 | Zhou et al. 2013 | model age | |
| Spot 2-1 | 207Pb-235U | 4.585 | 0.05 | Zhou et al. 2013 | model age | |
| Spot 2-2 | 207Pb-235U | 4.657 | 0.041 | Zhou et al. 2013 | model age | |
| Spot 3-1 | 207Pb-235U | 4.751 | 0.041 | Zhou et al. 2013 | model age | |
| Spot 3-2 | 207Pb-235U | 4.716 | 0.03 | Zhou et al. 2013 | model age | |
| Spot 3-3 | 207Pb-235U | 4.711 | 0.028 | Zhou et al. 2013 | model age | |
| Spot 4-1 | 207Pb-235U | 4.561 | 0.046 | Zhou et al. 2013 | model age | |
| Spot 4-2 | 207Pb-235U | 4.674 | 0.03 | Zhou et al. 2013 | model age | |
| Spot 4-3 | 207Pb-235U | 4.837 | 0.032 | Zhou et al. 2013 | model age | |
| Spot 4-4 | 207Pb-235U | 4.601 | 0.036 | Zhou et al. 2013 | model age | |
| Spot 5-1 | 207Pb-235U | 4.552 | 0.037 | Zhou et al. 2013 | model age | |
| Spot 5-2 | 207Pb-235U | 4.625 | 0.039 | Zhou et al. 2013 | model age | |
| Spot 6 | 207Pb-235U | 4.851 | 0.024 | Zhou et al. 2013 | model age | |
| Spot 7 | 207Pb-235U | 4.697 | 0.074 | Zhou et al. 2013 | model age | |
| zircons | U-Pb | 4.56 | Bukovanska and Ireland 1993 | model age | ||
| weighted average of 20 model ages determined on seven zircon grains | 206Pb-238U | 4.915 | 0.1 | Zhou et al. 2013 | model age | |
| Spot 1-1 | 206Pb-238U | 4.674 | 0.105 | Zhou et al. 2013 | model age | |
| Spot 1-2 | 206Pb-238U | 4.541 | 0.13 | Zhou et al. 2013 | model age | |
| Spot 1-3 | 206Pb-238U | 4.645 | 0.113 | Zhou et al. 2013 | model age | |
| Spot 1-4 | 206Pb-238U | 4.918 | 0.134 | Zhou et al. 2013 | model age | |
| Spot 1-5 | 206Pb-238U | 4.715 | 0.161 | Zhou et al. 2013 | model age | |
| Spot 1-6 | 206Pb-238U | 5.067 | 0.124 | Zhou et al. 2013 | model age | |
| Spot 1-7 | 206Pb-238U | 5.079 | 0.155 | Zhou et al. 2013 | model age | |
| Spot 2-1 | 206Pb-238U | 4.648 | 0.151 | Zhou et al. 2013 | model age | |
| Spot 2-2 | 206Pb-238U | 5.035 | 0.129 | Zhou et al. 2013 | model age | |
| Spot 3-1 | 206Pb-238U | 5.203 | 0.14 | Zhou et al. 2013 | model age | |
| Spot 3-2 | 206Pb-238U | 5.06 | 0.101 | Zhou et al. 2013 | model age | |
| Spot 3-3 | 206Pb-238U | 5.073 | 0.093 | Zhou et al. 2013 | model age | |
| Spot 4-1 | 206Pb-238U | 4.643 | 0.138 | Zhou et al. 2013 | model age | |
| Spot 4-2 | 206Pb-238U | 4.905 | 0.094 | Zhou et al. 2013 | model age | |
| Spot 4-3 | 206Pb-238U | 5.461 | 0.105 | Zhou et al. 2013 | model age | |
| Spot 4-4 | 206Pb-238U | 4.782 | 0.11 | Zhou et al. 2013 | model age | |
| Spot 5-1 | 206Pb-238U | 4.701 | 0.111 | Zhou et al. 2013 | model age | |
| Spot 5-2 | 206Pb-238U | 4.887 | 0.125 | Zhou et al. 2013 | model age | |
| Spot 6 | 206Pb-238U | 5.8 | 0.352 | Zhou et al. 2013 | model age | |
| Spot 7 | 206Pb-238U | 5.126 | 0.367 | Zhou et al. 2013 | model age | |
| Al-Mg | 4.5645 | 0.0004 | Schiller, Baker, and Bizzarro 2010 | model age | ||
| Pu-Xe | 4.551 | 0.015 | three samples | Shukolyukov and Begemann 1996a | model age | |
| Pu-Xe | 4.548 | 0.023 | Miura et al. 1998 | model age | ||
| Moama | ||||||
| average age of three extractions releasing 45–78% of 39Ar | Ar-Ar | 4.48 | 0.007 | Bogard and Garrison 2003 | plateau age | |
| sample at 350°C | Ar-Ar | 0.866 | 0.07 | Bogard and Garrison 2003 | extraction age | |
| sample at 400°C | Ar-Ar | 1.441 | 0.073 | Bogard and Garrison 2003 | extraction age | |
| sample at 500°C | Ar-Ar | 1.439 | 0.052 | Bogard and Garrison 2003 | extraction age | |
| sample at 600°C | Ar-Ar | 2.213 | 0.015 | Bogard and Garrison 2003 | extraction age | |
| sample at 675°C | Ar-Ar | 2.865 | 0.017 | Bogard and Garrison 2003 | extraction age | |
| sample at 725°C | Ar-Ar | 3.743 | 0.01 | Bogard and Garrison 2003 | extraction age | |
| sample at 775°C | Ar-Ar | 4.167 | 0.01 | Bogard and Garrison 2003 | extraction age | |
| sample at 810°C | Ar-Ar | 4.345 | 0.011 | Bogard and Garrison 2003 | extraction age | |
| sample at 847°C | Ar-Ar | 4.396 | 0.012 | Bogard and Garrison 2003 | extraction age | |
| sample at 880°C | Ar-Ar | 4.426 | 0.012 | Bogard and Garrison 2003 | extraction age | |
| sample at 900°C | Ar-Ar | 4.473 | 0.012 | Bogard and Garrison 2003 | extraction age | |
| sample at 915°C | Ar-Ar | 4.484 | 0.012 | Bogard and Garrison 2003 | extraction age | |
| sample at 925°C | Ar-Ar | 4.483 | 0.011 | Bogard and Garrison 2003 | extraction age | |
| sample at 940°C | Ar-Ar | 4.447 | 0.009 | Bogard and Garrison 2003 | extraction age | |
| sample at 975°C | Ar-Ar | 4.363 | 0.011 | Bogard and Garrison 2003 | extraction age | |
| sample at 1025°C | Ar-Ar | 4.181 | 0.012 | Bogard and Garrison 2003 | extraction age | |
| sample at 1100°C | Ar-Ar | 4.217 | 0.018 | Bogard and Garrison 2003 | extraction age | |
| sample at 1200°C | Ar-Ar | 4.133 | 0.042 | Bogard and Garrison 2003 | extraction age | |
| sample at 1350°C | Ar-Ar | 4.294 | 0.107 | Bogard and Garrison 2003 | extraction age | |
| sample at 1600°C | Ar-Ar | 4.209 | 0.188 | Bogard and Garrison 2003 | extraction age | |
| Moore County | ||||||
| whole-rock samples | K-Ar | 3.5 | Heymann, Mazor, and Anders 1968 | model age | ||
| K-Ar | 4.46 | Shukolyukov and Begemann 1996b | model age | |||
| 45–100% extractions | Ar-Ar | 4.25 | 0.03 | Bogard and Garrison 2003 | plateau age | |
| 350°C | Ar-Ar | 6.742 | 0.02 | Bogard and Garrison 2003 | step extraction age | |
| 425°C | Ar-Ar | 4.542 | 0.3 | Bogard and Garrison 2003 | step extraction age | |
| 500°C | Ar-Ar | 2.102 | 0.315 | Bogard and Garrison 2003 | step extraction age | |
| 550°C | Ar-Ar | 1.827 | 0.348 | Bogard and Garrison 2003 | step extraction age | |
| 625°C | Ar-Ar | 3.21 | 0.074 | Bogard and Garrison 2003 | step extraction age | |
| 700°C | Ar-Ar | 3.029 | 0.049 | Bogard and Garrison 2003 | step extraction age | |
| 750°C | Ar-Ar | 4.083 | 0.03 | Bogard and Garrison 2003 | step extraction age | |
| 800°C | Ar-Ar | 4.196 | 0.016 | Bogard and Garrison 2003 | step extraction age | |
| 830°C | Ar-Ar | 4.23 | 0.015 | Bogard and Garrison 2003 | step extraction age | |
| 852°C | Ar-Ar | 4.217 | 0.018 | Bogard and Garrison 2003 | step extraction age | |
| 875°C | Ar-Ar | 4.223 | 0.014 | Bogard and Garrison 2003 | step extraction age | |
| 895°C | Ar-Ar | 4.197 | 0.015 | Bogard and Garrison 2003 | step extraction age | |
| 920°C | Ar-Ar | 4.215 | 0.014 | Bogard and Garrison 2003 | step extraction age | |
| 950°C | Ar-Ar | 4.204 | 0.014 | Bogard and Garrison 2003 | step extraction age | |
| 975°C | Ar-Ar | 4.231 | 0.008 | Bogard and Garrison 2003 | step extraction age | |
| 1000°C | Ar-Ar | 4.25 | 0.008 | Bogard and Garrison 2003 | step extraction age | |
| 1025°C | Ar-Ar | 4.245 | 0.007 | Bogard and Garrison 2003 | step extraction age | |
| 1050°C | Ar-Ar | 4.218 | 0.008 | Bogard and Garrison 2003 | step extraction age | |
| 1100°C | Ar-Ar | 4.22 | 0.009 | Bogard and Garrison 2003 | step extraction age | |
| 1150°C | Ar-Ar | 4.189 | 0.01 | Bogard and Garrison 2003 | step extraction age | |
| 1155°C | Ar-Ar | 4.157 | 0.04 | Bogard and Garrison 2003 | step extraction age | |
| 1225°C | Ar-Ar | 4.117 | 0.03 | Bogard and Garrison 2003 | step extraction age | |
| 1325°C | Ar-Ar | 4.229 | 0.017 | Bogard and Garrison 2003 | step extraction age | |
| 1425°C | Ar-Ar | 4.267 | 0.008 | Bogard and Garrison 2003 | step extraction age | |
| 1500°C | Ar-Ar | 4.255 | 0.018 | Bogard and Garrison 2003 | step extraction age | |
| 1600°C | Ar-Ar | 4.272 | 0.61 | Bogard and Garrison 2003 | step extraction age | |
| Pu-Xe | 4.548 | Shukolyukov and Begemann 1996a | model age | |||
| Pasamonte | ||||||
| whole rock samples | K-Ar | 3.5 | Heymann, Mazor, and Anders 1968 | model age | ||
| high temperature, based on last fraction extracted | K-Ar | 4.51 | 0.065 | Podosek and Huneke 1973 | model age | |
| 545°C extraction | K-Ar | 3.595 | 0.062 | Podosek and Huneke 1973 | model age | |
| 630°C extraction | K-Ar | 3.902 | 0.02 | Podosek and Huneke 1973 | model age | |
| 745°C extraction | K-Ar | 4.066 | 0.005 | Podosek and Huneke 1973 | model age | |
| 850°C extraction | K-Ar | 4.069 | 0.004 | Podosek and Huneke 1973 | model age | |
| 935°C extraction | K-Ar | 4.132 | 0.006 | Podosek and Huneke 1973 | model age | |
| 1040°C extraction | K-Ar | 4.119 | 0.006 | Podosek and Huneke 1973 | model age | |
| 1195°C extraction | K-Ar | 4.364 | 0.009 | Podosek and Huneke 1973 | model age | |
| 1515°C extraction | K-Ar | 4.511 | 0.015 | Podosek and Huneke 1973 | model age | |
| bulk plateau age, based on the first 80% Ar extracted | Ar-Ar | 4.15 | 0.3 | Podosek and Huneke 1973 | plateau age | |
| low temperature | Ar-Ar | 4 | 0.05 | Kunz et al. 1995 | spectra model age | |
| high temperature, 75% gas loss | Ar-Ar | 4.4 | 0.1 | Kunz et al. 1995 | spectra model age | |
| sample 1, low temperature | Ar-Ar | 3.9 | 0.1 | Kunz et al. 1995 | spectrum model age | |
| sample 1, high temperature, 90% gas loss | Ar-Ar | 4.4 | 0.1 | Kunz et al. 1995 | spectrum model age | |
| sample 5, low temperature | Ar-Ar | 4.1 | 0.05 | Kunz et al. 1995 | spectrum model age | |
| sample 5, high temperature, 70% gas loss | Ar-Ar | 4.4 | 0.1 | Kunz et al. 1995 | spectrum model age | |
| 300°C | Ar-Ar | 7.79 | 2.455 | Kunz et al. 1995 | extraction age | |
| 400°C | Ar-Ar | 6.836 | 0.202 | Kunz et al. 1995 | extraction age | |
| 470°C | Ar-Ar | 4.447 | 0.05 | Kunz et al. 1995 | extraction age | |
| 540°C | Ar-Ar | 4.065 | 0.034 | Kunz et al. 1995 | extraction age | |
| 600°C | Ar-Ar | 4.163 | 0.02 | Kunz et al. 1995 | extraction age | |
| 630°C | Ar-Ar | 4.241 | 0.022 | Kunz et al. 1995 | extraction age | |
| 670°C | Ar-Ar | 3.803 | 0.015 | Kunz et al. 1995 | extraction age | |
| 700°C | Ar-Ar | 3.898 | 0.013 | Kunz et al. 1995 | extraction age | |
| 730°C | Ar-Ar | 3.875 | 0.013 | Kunz et al. 1995 | extraction age | |
| 760°C | Ar-Ar | 3.921 | 0.014 | Kunz et al. 1995 | extraction age | |
| 790°C | Ar-Ar | 3.921 | 0.01 | Kunz et al. 1995 | extraction age | |
| 810°C | Ar-Ar | 3.938 | 0.009 | Kunz et al. 1995 | extraction age | |
| 830°C | Ar-Ar | 3.996 | 0.01 | Kunz et al. 1995 | extraction age | |
| 850°C | Ar-Ar | 3.989 | 0.014 | Kunz et al. 1995 | extraction age | |
| 880°C | Ar-Ar | 4.02 | 0.016 | Kunz et al. 1995 | extraction age | |
| 910°C | Ar-Ar | 4.024 | 0.011 | Kunz et al. 1995 | extraction age | |
| 940°C | Ar-Ar | 4.041 | 0.013 | Kunz et al. 1995 | extraction age | |
| 980°C | Ar-Ar | 4.08 | 0.016 | Kunz et al. 1995 | extraction age | |
| 1020°C | Ar-Ar | 4.162 | 0.026 | Kunz et al. 1995 | extraction age | |
| 1070°C | Ar-Ar | 4.184 | 0.019 | Kunz et al. 1995 | extraction age | |
| 1120°C | Ar-Ar | 4.21 | 0.027 | Kunz et al. 1995 | extraction age | |
| 1160°C | Ar-Ar | 4.314 | 0.048 | Kunz et al. 1995 | extraction age | |
| 1200°C | Ar-Ar | 4.325 | 0.041 | Kunz et al. 1995 | extraction age | |
| 1240°C | Ar-Ar | 4.438 | 0.069 | Kunz et al. 1995 | extraction age | |
| 1340°C | Ar-Ar | 4.348 | 0.029 | Kunz et al. 1995 | extraction age | |
| 1440°C | Ar-Ar | 4.397 | 0.015 | Kunz et al. 1995 | extraction age | |
| 1580°C | Ar-Ar | 4.443 | 0.072 | Kunz et al. 1995 | extraction age | |
| 300°C | Ar-Ar | 6.458 | 0.655 | Kunz et al. 1995 | extraction age | |
| 350°C | Ar-Ar | 5.442 | 0.189 | Kunz et al. 1995 | extraction age | |
| 400°C | Ar-Ar | 4.402 | 0.073 | Kunz et al. 1995 | extraction age | |
| 450°C | Ar-Ar | 4.189 | 0.032 | Kunz et al. 1995 | extraction age | |
| 500°C | Ar-Ar | 4.331 | 0.019 | Kunz et al. 1995 | extraction age | |
| 550°C | Ar-Ar | 4.487 | 0.013 | Kunz et al. 1995 | extraction age | |
| 600°C | Ar-Ar | 4.209 | 0.005 | Kunz et al. 1995 | extraction age | |
| 640°C | Ar-Ar | 4.1 | 0.004 | Kunz et al. 1995 | extraction age | |
| 680°C | Ar-Ar | 4.1 | 0.004 | Kunz et al. 1995 | extraction age | |
| 700°C | Ar-Ar | 4.105 | 0.005 | Kunz et al. 1995 | extraction age | |
| 720°C | Ar-Ar | 4.13 | 0.004 | Kunz et al. 1995 | extraction age | |
| 740°C | Ar-Ar | 4.14 | 0.005 | Kunz et al. 1995 | extraction age | |
| 760°C | Ar-Ar | 4.148 | 0.004 | Kunz et al. 1995 | extraction age | |
| 780°C | Ar-Ar | 4.176 | 0.006 | Kunz et al. 1995 | extraction age | |
| 800°C | Ar-Ar | 4.195 | 0.004 | Kunz et al. 1995 | extraction age | |
| 820°C | Ar-Ar | 4.203 | 0.006 | Kunz et al. 1995 | extraction age | |
| 840°C | Ar-Ar | 4.218 | 0.006 | Kunz et al. 1995 | extraction age | |
| 860°C | Ar-Ar | 4.24 | 0.005 | Kunz et al. 1995 | extraction age | |
| 890°C | Ar-Ar | 4.241 | 0.006 | Kunz et al. 1995 | extraction age | |
| 920°C | Ar-Ar | 4.217 | 0.006 | Kunz et al. 1995 | extraction age | |
| 950°C | Ar-Ar | 4.223 | 0.008 | Kunz et al. 1995 | extraction age | |
| 990°C | Ar-Ar | 4.305 | 0.009 | Kunz et al. 1995 | extraction age | |
| 1030°C | Ar-Ar | 4.357 | 0.011 | Kunz et al. 1995 | extraction age | |
| 1080°C | Ar-Ar | 4.381 | 0.014 | Kunz et al. 1995 | extraction age | |
| 1150°C | Ar-Ar | 4.436 | 0.006 | Kunz et al. 1995 | extraction age | |
| 1230°C | Ar-Ar | 4.483 | 0.007 | Kunz et al. 1995 | extraction age | |
| 1270°C | Ar-Ar | 4.567 | 0.066 | Kunz et al. 1995 | extraction age | |
| 1310°C | Ar-Ar | 5.407 | 0.341 | Kunz et al. 1995 | extraction age | |
| 1380°C | Ar-Ar | 4.666 | 0.222 | Kunz et al. 1995 | extraction age | |
| 300°C | Ar-Ar | 6.191 | 0.948 | Kunz et al. 1995 | extraction age | |
| 450°C | Ar-Ar | 6.099 | 0.169 | Kunz et al. 1995 | extraction age | |
| 530°C | Ar-Ar | 4.637 | 0.121 | Kunz et al. 1995 | extraction age | |
| 600°C | Ar-Ar | 4.477 | 0.077 | Kunz et al. 1995 | extraction age | |
| 670°C | Ar-Ar | 4.698 | 0.031 | Kunz et al. 1995 | extraction age | |
| 730°C | Ar-Ar | 4.007 | 0.027 | Kunz et al. 1995 | extraction age | |
| 790°C | Ar-Ar | 3.997 | 0.022 | Kunz et al. 1995 | extraction age | |
| 830°C | Ar-Ar | 4.076 | 0.021 | Kunz et al. 1995 | extraction age | |
| 880°C | Ar-Ar | 4.23 | 0.021 | Kunz et al. 1995 | extraction age | |
| 940°C | Ar-Ar | 4.267 | 0.022 | Kunz et al. 1995 | extraction age | |
| 1020°C | Ar-Ar | 4.221 | 0.016 | Kunz et al. 1995 | extraction age | |
| 1120°C | Ar-Ar | 4.255 | 0.023 | Kunz et al. 1995 | extraction age | |
| 1200°C | Ar-Ar | 4.287 | 0.083 | Kunz et al. 1995 | extraction age | |
| 1320°C | Ar-Ar | 4.437 | 0.033 | Kunz et al. 1995 | extraction age | |
| 1440°C | Ar-Ar | 4.739 | 0.385 | Kunz et al. 1995 | extraction age | |
| sample 7 plateau | Ar-Ar | 4.245 | 0.024 | Kunz et al. 1995 | plateau age | |
| sample 7, low temperature, 48% width | Ar-Ar | 4 | 0.1 | Kunz et al. 1995 | spectrum model age | |
| sample 7, high temperature, 35% gas loss | Ar-Ar | 4.4 | 0.1 | Kunz et al. 1995 | spectrum model age | |
| Revised Podosek and Huneke 1973 age | Ar-Ar | 4.02 | Quitté, Birck, and Allègre 2000 | plateau age | ||
| 207Pb-206Pb | 4.573 | 0.006 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.572 | 0.005 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.484 | 0.004 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.454 | 0.01 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.963 | 0.03 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.912 | 0.01 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.709 | 0.008 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.664 | 0.006 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.515 | 0.06 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.454 | 0.019 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.457 | 0.012 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.51 | 0.1 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.468 | 0.015 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.44 | 0.023 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.535 | 0.005 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.534 | 0.004 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.542 | 0.019 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.534 | 0.02 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.534 | 0.013 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.519 | 0.013 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.555 | 0.017 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-206Pb | 4.52 | 0.004 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 4.874 | 0.038 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 4.814 | 0.038 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 5.694 | 0.083 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 5.597 | 0.092 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 3.38 | 0.35 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 5.336 | 0.7 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 0.296 | 0.005 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 0.277 | 0.003 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 0.103 | 0.009 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 0.377 | 0.014 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 0.376 | 0.016 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 2.953 | 0.3 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 3.29 | 0.085 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 3.215 | 0.107 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 4.903 | 0.041 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 4.907 | 0.041 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 4.522 | 0.14 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 4.5 | 0.15 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 1.851 | 0.031 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 1.477 | 0.03 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 1.798 | 0.043 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 206Pb-238U | 3.39 | 0.027 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.663 | 0.015 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.645 | 0.015 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.806 | 0.031 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.784 | 0.044 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.421 | 0.175 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 5.032 | 0.23 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 1.724 | 0.015 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 1.644 | 0.011 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 0.865 | 0.085 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 1.786 | 0.053 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 1.784 | 0.072 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 3.955 | 0.195 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.061 | 0.06 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.014 | 0.08 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.645 | 0.014 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.646 | 0.016 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.536 | 0.06 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.523 | 0.068 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 3.419 | 0.027 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 3.161 | 0.036 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 3.396 | 0.036 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 207Pb-235U | 4.136 | 0.015 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 208Pb-232Th | 4.678 | 0.085 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 208Pb-232Th | 14.8 | 0.6 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 208Pb-232Th | 9.6 | Unruh, Nakamura, and Tatsumoto 1977 | model age | |||
| 208Pb-232Th | 0.295 | 0.03 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 208Pb-232Th | 0.57 | 0.2 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 208Pb-232Th | 4.922 | 0.5 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 208Pb-232Th | 4.16 | 0.25 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 208Pb-232Th | 10.7 | Unruh, Nakamura, and Tatsumoto 1977 | model age | |||
| 208Pb-232Th | 3.597 | 0.099 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 208Pb-232Th | 3.549 | 0.16 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| 208Pb-232Th | 8.627 | 0.35 | Unruh, Nakamura, and Tatsumoto 1977 | model age | ||
| two samples | Pu-Xe | 4.576 | 0.019 | Shukolyukov and Begemann 1996a | model age | |
| Serra De Magé | ||||||
| whole rock samples | K-Ar | 2.7 | Heymann, Mazor, and Anders 1968 | model age | ||
| average of four extractions having the same age within uncertainties | Ar-Ar | 3.386 | 0.007 | Bogard and Garrison 2003 | plateau age | |
| 350°C | Ar-Ar | 6.1 | 0.114 | Bogard and Garrison 2003 | step extraction model age | |
| 450°C | Ar-Ar | 2.548 | 0.191 | Bogard and Garrison 2003 | step extraction model age | |
| 525°C | Ar-Ar | 1.231 | 0.25 | Bogard and Garrison 2003 | step extraction model age | |
| 600°C | Ar-Ar | 1.77 | 0.122 | Bogard and Garrison 2003 | step extraction model age | |
| 650°C | Ar-Ar | 0.499 | 0.199 | Bogard and Garrison 2003 | step extraction model age | |
| 700°C | Ar-Ar | 2.779 | 0.18 | Bogard and Garrison 2003 | step extraction model age | |
| 775°C | Ar-Ar | 3.112 | 0.093 | Bogard and Garrison 2003 | step extraction model age | |
| 825°C | Ar-Ar | 3.316 | 0.033 | Bogard and Garrison 2003 | step extraction model age | |
| 875°C | Ar-Ar | 3.387 | 0.037 | Bogard and Garrison 2003 | step extraction model age | |
| 925°C | Ar-Ar | 3.372 | 0.045 | Bogard and Garrison 2003 | step extraction model age | |
| 975°C | Ar-Ar | 3.388 | 0.06 | Bogard and Garrison 2003 | step extraction model age | |
| 1025°C | Ar-Ar | 3.395 | 0.041 | Bogard and Garrison 2003 | step extraction model age | |
| 1075°C | Ar-Ar | 3.461 | 0.045 | Bogard and Garrison 2003 | step extraction model age | |
| 1125°C | Ar-Ar | 3.511 | 0.037 | Bogard and Garrison 2003 | step extraction model age | |
| 1175°C | Ar-Ar | 3.619 | 0.048 | Bogard and Garrison 2003 | step extraction model age | |
| 1225°C | Ar-Ar | 3.528 | 0.103 | Bogard and Garrison 2003 | step extraction model age | |
| 1275°C | Ar-Ar | 3.585 | 0.158 | Bogard and Garrison 2003 | step extraction model age | |
| 1325°C | Ar-Ar | 3.689 | 0.193 | Bogard and Garrison 2003 | step extraction model age | |
| 1400°C | Ar-Ar | 3.783 | 0.053 | Bogard and Garrison 2003 | step extraction model age | |
| 1500°C | Ar-Ar | 3.91 | 0.028 | Bogard and Garrison 2003 | step extraction model age | |
| Stannern | ||||||
| whole-rock samples | K-Ar | 3.8 | Heymann, Mazor, and Anders 1968 | model age | ||
| 545°C | K-Ar | 3.86 | 0.028 | Podosek and Huneke 1973 | step model age | |
| 630°C | K-Ar | 3.837 | 0.008 | Podosek and Huneke 1973 | step model age | |
| 745°C | K-Ar | 3.704 | 0.003 | Podosek and Huneke 1973 | step model age | |
| 850°C | K-Ar | 3.472 | 0.002 | Podosek and Huneke 1973 | step model age | |
| 935°C | K-Ar | 3.514 | 0.007 | Podosek and Huneke 1973 | step model age | |
| 1040°C | K-Ar | 3.64 | 0.003 | Podosek and Huneke 1973 | step model age | |
| 1195°C | K-Ar | 3.591 | 0.003 | Podosek and Huneke 1973 | step model age | |
| 1515°C | K-Ar | 3.923 | 0.006 | Podosek and Huneke 1973 | step model age | |
| K-Ar | 3.57 | mean of ages in literature | Shukolyukov and Begemann 1996a | model age | ||
| Ar-Ar | 3.7 | 0.2 | based on nine extractions at stepped temperatures | Podosek and Huneke 1973 | plateau age | |
| three samples, low temperature | Ar-Ar | 3.3 | 0.3 | Kunz et al. 1995 | plateau age | |
| three samples, high temperature, 80% gas loss | Ar-Ar | 4 | 0.2 | Kunz et al. 1995 | plateau age | |
| drill core 1, basalt clast, 300°C | Ar-Ar | 6.313 | 0.181 | Kunz et al. 1995 | step extraction age | |
| 350°C | Ar-Ar | 3.632 | 0.028 | Kunz et al. 1995 | step extraction age | |
| 400°C | Ar-Ar | 3.09 | 0.014 | Kunz et al. 1995 | step extraction age | |
| 450°C | Ar-Ar | 3.564 | 0.008 | Kunz et al. 1995 | step extraction age | |
| 500°C | Ar-Ar | 3.687 | 0.005 | Kunz et al. 1995 | step extraction age | |
| 550°C | Ar-Ar | 3.679 | 0.005 | Kunz et al. 1995 | step extraction age | |
| 580°C | Ar-Ar | 3.636 | 0.004 | Kunz et al. 1995 | step extraction age | |
| 600°C | Ar-Ar | 3.523 | 0.005 | Kunz et al. 1995 | step extraction age | |
| 620°C | Ar-Ar | 3.48 | 0.007 | Kunz et al. 1995 | step extraction age | |
| 640°C | Ar-Ar | 3.392 | 0.005 | Kunz et al. 1995 | step extraction age | |
| 670°C | Ar-Ar | 3.408 | 0.005 | Kunz et al. 1995 | step extraction age | |
| 690°C | Ar-Ar | 3.471 | 0.006 | Kunz et al. 1995 | step extraction age | |
| 710°C | Ar-Ar | 3.511 | 0.005 | Kunz et al. 1995 | step extraction age | |
| 740°C | Ar-Ar | 3.543 | 0.005 | Kunz et al. 1995 | step extraction age | |
| 770°C | Ar-Ar | 3.58 | 0.006 | Kunz et al. 1995 | step extraction age | |
| 810°C | Ar-Ar | 3.597 | 0.006 | Kunz et al. 1995 | step extraction age | |
| 850°C | Ar-Ar | 3.595 | 0.006 | Kunz et al. 1995 | step extraction age | |
| 890°C | Ar-Ar | 3.57 | 0.006 | Kunz et al. 1995 | step extraction age | |
| 930°C | Ar-Ar | 3.537 | 0.006 | Kunz et al. 1995 | step extraction age | |
| 970°C | Ar-Ar | 3.478 | 0.007 | Kunz et al. 1995 | step extraction age | |
| 1020°C | Ar-Ar | 3.298 | 0.007 | Kunz et al. 1995 | step extraction age | |
| 1070°C | Ar-Ar | 3.474 | 0.012 | Kunz et al. 1995 | step extraction age | |
| 1120°C | Ar-Ar | 3.785 | 0.017 | Kunz et al. 1995 | step extraction age | |
| 1170°C | Ar-Ar | 4.003 | 0.013 | Kunz et al. 1995 | step extraction age | |
| 1220°C | Ar-Ar | 4.141 | 0.024 | Kunz et al. 1995 | step extraction age | |
| 1270°C | Ar-Ar | 4.229 | 0.026 | Kunz et al. 1995 | step extraction age | |
| 1330°C | Ar-Ar | 4.338 | 0.069 | Kunz et al. 1995 | step extraction age | |
| 1400°C | Ar-Ar | 4.247 | 0.049 | Kunz et al. 1995 | step extraction age | |
| drill core 2, recrystallized classic matrix 300°C | Ar-Ar | 4.76 | 0.601 | Kunz et al. 1995 | step extraction age | |
| 350°C | Ar-Ar | 3.672 | 0.069 | Kunz et al. 1995 | step extraction age | |
| 400°C | Ar-Ar | 3.238 | 0.022 | Kunz et al. 1995 | step extraction age | |
| 450°C | Ar-Ar | 3.588 | 0.011 | Kunz et al. 1995 | step extraction age | |
| 500°C | Ar-Ar | 3.747 | 0.009 | Kunz et al. 1995 | step extraction age | |
| 540°C | Ar-Ar | 3.715 | 0.008 | Kunz et al. 1995 | step extraction age | |
| 580°C | Ar-Ar | 3.88 | 0.006 | Kunz et al. 1995 | step extraction age | |
| 600°C | Ar-Ar | 3.596 | 0.01 | Kunz et al. 1995 | step extraction age | |
| 620°C | Ar-Ar | 3.5 | 0.005 | Kunz et al. 1995 | step extraction age | |
| 640°C | Ar-Ar | 3.405 | 0.007 | Kunz et al. 1995 | step extraction age | |
| 670°C | Ar-Ar | 3.402 | 0.007 | Kunz et al. 1995 | step extraction age | |
| 690°C | Ar-Ar | 3.448 | 0.007 | Kunz et al. 1995 | step extraction age | |
| 710°C | Ar-Ar | 3.5 | 0.008 | Kunz et al. 1995 | step extraction age | |
| 740°C | Ar-Ar | 3.543 | 0.009 | Kunz et al. 1995 | step extraction age | |
| 770°C | Ar-Ar | 3.558 | 0.01 | Kunz et al. 1995 | step extraction age | |
| 810°C | Ar-Ar | 3.545 | 0.01 | Kunz et al. 1995 | step extraction age | |
| 850°C | Ar-Ar | 3.487 | 0.011 | Kunz et al. 1995 | step extraction age | |
| 890°C | Ar-Ar | 3.432 | 0.013 | Kunz et al. 1995 | step extraction age | |
| 930°C | Ar-Ar | 3.382 | 0.012 | Kunz et al. 1995 | step extraction age | |
| 970°C | Ar-Ar | 3.282 | 0.014 | Kunz et al. 1995 | step extraction age | |
| 1020°C | Ar-Ar | 3.095 | 0.014 | Kunz et al. 1995 | step extraction age | |
| 1070°C | Ar-Ar | 3.146 | 0.027 | Kunz et al. 1995 | step extraction age | |
| 1120°C | Ar-Ar | 3.492 | 0.05 | Kunz et al. 1995 | step extraction age | |
| 1170°C | Ar-Ar | 3.735 | 0.065 | Kunz et al. 1995 | step extraction age | |
| 1220°C | Ar-Ar | 4.001 | 0.114 | Kunz et al. 1995 | step extraction age | |
| 1270°C | Ar-Ar | 3.947 | 0.077 | Kunz et al. 1995 | step extraction age | |
| 1330°C | Ar-Ar | 4.122 | 0.126 | Kunz et al. 1995 | step extraction age | |
| 1400°C | Ar-Ar | 3.84 | 0.327 | Kunz et al. 1995 | step extraction age | |
| Pb-Pb | 4.329 | Manhès et al. 1975 | model age | |||
| Pb-Pb | 4.13 | Tera, Carlson, and Boctor 1987 | model age | |||
| Pu-Xe | 4.46 | 0.028 | Shukolyukov and Begemann 1996a | model age | ||
| Pu-Xe | 4.434 | 0.013 | Miura et al. 1998 | model age | ||
| Yamato 75011 | ||||||
| whole rock sample | K-Ar | 4 | 0.5 | Miura et al. 1993 | model age | |
| 84 matrix, 11 extractions | Ar-Ar | 3.94 | 0.04 | Takeda, Mori, and Bogard 1994 | plateau age | |
| 84 clast, 11 extractions | Ar-Ar | 3.98 | 0.03 | Takeda, Mori, and Bogard 1994 | plateau age | |
| 84 matrix, temp. 300 | Ar-Ar | 3.76 | 0.05 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 400 | Ar-Ar | 3.95 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 500 | Ar-Ar | 4.01 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 600 | Ar-Ar | 3.96 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 700 | Ar-Ar | 3.97 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 775 | Ar-Ar | 3.95 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 850 | Ar-Ar | 3.88 | 0.04 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 950 | Ar-Ar | 3.91 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 1000 | Ar-Ar | 3.94 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 1050 | Ar-Ar | 3.97 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 1100 | Ar-Ar | 3.98 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 1150 | Ar-Ar | 3.98 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 1225 | Ar-Ar | 4.12 | 0.03 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 1350 | Ar-Ar | 4.35 | 0.03 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 matrix, temp. 1500 | Ar-Ar | 4.2 | 0.16 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 300 | Ar-Ar | 3.99 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 400 | Ar-Ar | 3.69 | 0.03 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 500 | Ar-Ar | 4.05 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 575 | Ar-Ar | 3.83 | 0.06 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 650 | Ar-Ar | 3.99 | 0.03 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 725 | Ar-Ar | 4.03 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 800 | Ar-Ar | 3.97 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 850 | Ar-Ar | 3.98 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 900 | Ar-Ar | 3.96 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 950 | Ar-Ar | 3.96 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 1000 | Ar-Ar | 3.99 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 1050 | Ar-Ar | 4.08 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 1100 | Ar-Ar | 4.15 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 1150 | Ar-Ar | 4.23 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 1225 | Ar-Ar | 4.36 | 0.03 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 1300 | Ar-Ar | 4.48 | 0.03 | Takeda, Mori, and Bogard 1994 | degassing age | |
| 84 clast, temp. 1500 | Ar-Ar | 4.5 | 0.02 | Takeda, Mori, and Bogard 1994 | degassing age | |
| matrix, low temperature | Ar-Ar | 3.91 | 0.04 | Kunz et al. 1995 | spectrum model age | |
| matrix, high temperature, 90% gas extraction | Ar-Ar | 4.4 | 0.1 | Kunz et al. 1995 | spectrum model age | |
| clast, low temperature | Ar-Ar | 3.98 | 0.03 | Kunz et al. 1995 | spectrum model age | |
| clast, high temperature, 90% gas extraction | Ar-Ar | 4.5 | 0.1 | Kunz et al. 1995 | spectrum model age | |
| 73 matrix, whole rock, BABI | Rb-Sr | 4.28 | 0.24 | Nyquist et al. 1986 | model age | |
| 73 matrix, <2.45 g/cu. cm., BABI | Rb-Sr | 4.53 | 0.07 | Nyquist et al. 1986 | model age | |
| 73 matrix, 2.45–2.85 g/cu. cm., BABI | Rb-Sr | 3.91 | 0.4 | Nyquist et al. 1986 | model age | |
| 73 matrix, 2.85–3.3 g/cu. cm., BABI | Rb-Sr | 4.71 | 0.19 | Nyquist et al. 1986 | model age | |
| 73 matrix, 3.3 g/cu. cm., BABI | Rb-Sr | 4.73 | 0.31 | Nyquist et al. 1996 | model age | |
| 84B clast, whole rock 1, BABI | Rb-Sr | 4.34 | 0.89 | Nyquist et al. 1986 | model age | |
| 84B clast, whole rock 3, BABI | Rb-Sr | 4.36 | 0.29 | Nyquist et al. 1986 | model age | |
| 84B clast, <2.45 g/cu. cm., BABI | Rb-Sr | 4.57 | 0.05 | Nyquist et al. 1986 | model age | |
| 84B clast, 2.45–2.65 g/cu. cm., BABI | Rb-Sr | 4.52 | 0.15 | Nyquist et al. 1986 | model age | |
| 84B clast, 2.65–2.85 g/cu. cm., BABI | Rb-Sr | 3.55 | 0.51 | Nyquist et al. 1986 | model age | |
| 84B clast, Plag, BABI | Rb-Sr | 3.73 | 0.54 | Nyquist et al. 1986 | model age | |
| 84B clast, Lt. Px, BABI | Rb-Sr | 4.11 | 0.11 | Nyquist et al. 1986 | model age | |
| 84B clast, Dk. Px, BABI | Rb-Sr | 4.51 | 0.14 | Nyquist et al. 1986 | model age | |
| 84B clast, most Mag, BABI | Rb-Sr | 4.66 | 0.12 | Nyquist et al. 1986 | model age | |
| zircon 011-1a | 207Pb-206Pb | 4.551 | 0.008 | Misawa, Yamaguchi, and Kaiden 2005 | model age | |
| zircon 011-1b | 207Pb-206Pb | 4.561 | 0.02 | Misawa, Yamaguchi, and Kaiden 2005 | model age | |
| zircon 011-2a | 207Pb-206Pb | 4.552 | 0.01 | Misawa, Yamaguchi, and Kaiden 2005 | model age | |
| zircon 011-2b | 207Pb-206Pb | 4.549 | 0.009 | Misawa, Yamaguchi, and Kaiden 2005 | model age | |
| zircon 011-2c | 207Pb-206Pb | 4.543 | 0.013 | Misawa, Yamaguchi, and Kaiden 2005 | model age | |
| zircon 011-1a | 206Pb-238U | 5.04 | 0.078 | Misawa, Yamaguchi, and Kaiden 2005 | model age | |
| zircon 011-1b | 206Pb-238U | 4.816 | 0.079 | Misawa, Yamaguchi, and Kaiden 2005 | model age | |
| zircon 011-2a | 206Pb-238U | 4.548 | 0.047 | Misawa, Yamaguchi, and Kaiden 2005 | model age | |
| zircon 011-2b | 206Pb-238U | 4.842 | 0.073 | Misawa, Yamaguchi, and Kaiden 2005 | model age | |
| zircon 011-2c | 206Pb-238U | 5.07 | 0.064 | Misawa, Yamaguchi, and Kaiden 2005 | model age | |
| 73 matrix, whole rock, chondrite | Sm-Nd | 4.55 | 0.03 | Nyquist et al. 1986 | model age | |
| 73 matrix, 2.45–2.85 g/cu. cm., chondrite | Sm-Nd | 4.52 | 0.03 | Nyquist et al. 1986 | model age | |
| 73 matrix, 2.85–3.3 g/cu. cm., chondrite | Sm-Nd | 4.53 | 0.02 | Nyquist et al. 1986 | model age | |
| 73 matrix, 3.3 g/cu. cm., chondrite | Sm-Nd | 4.51 | 0.02 | Nyquist et al. 1996 | model age | |
| 84B clast, whole rock 1, chondrite | Sm-Nd | 4.55 | 0.02 | Nyquist et al. 1986 | model age | |
| 84B clast, whole rock 3, chondrite | Sm-Nd | 4.54 | 0.02 | Nyquist et al. 1986 | model age | |
| 84B clast, <2.45 g/cu. cm., chondrite | Sm-Nd | 4.51 | 0.04 | Nyquist et al. 1986 | model age | |
| 84B clast, Plag, chondrite | Sm-Nd | 4.56 | 0.04 | Nyquist et al. 1986 | model age | |
| 84B clast, Lt. Px, chondrite | Sm-Nd | 4.56 | 0.02 | Nyquist et al. 1986 | model age | |
| 84B clast, Dk. Px, chondrite | Sm-Nd | 4.53 | 0.02 | Nyquist et al. 1986 | model age | |
| 84B clast, most Mag, chondrite | Sm-Nd | 4.58 | 0.02 | Nyquist et al. 1986 | model age | |
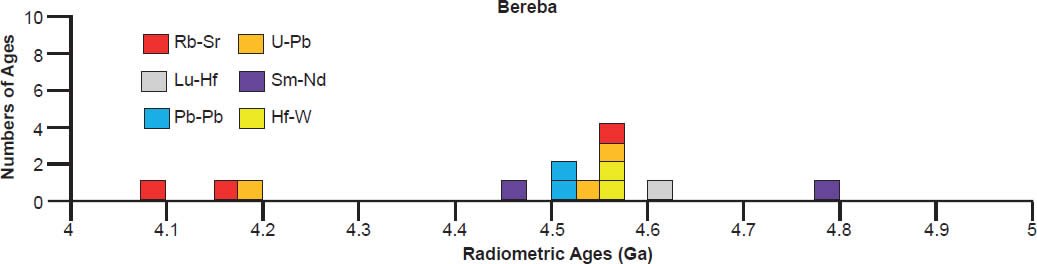
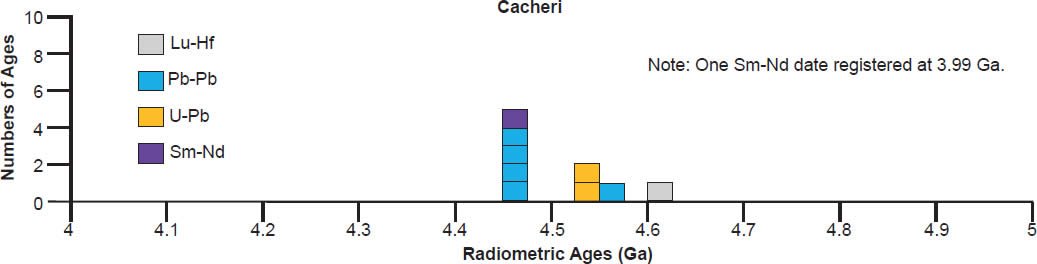
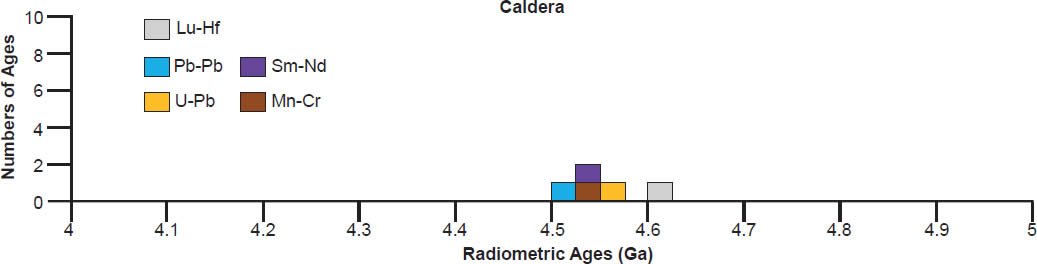
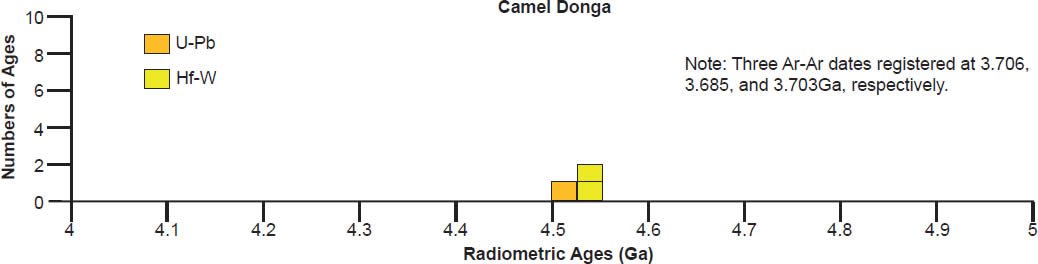
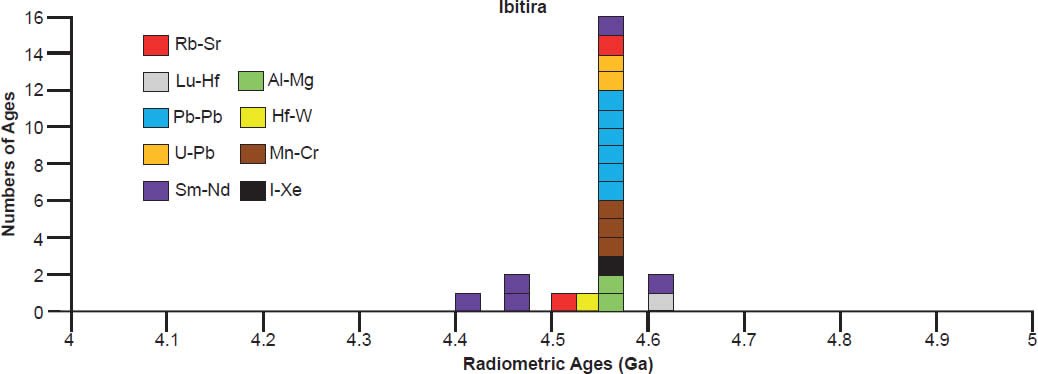
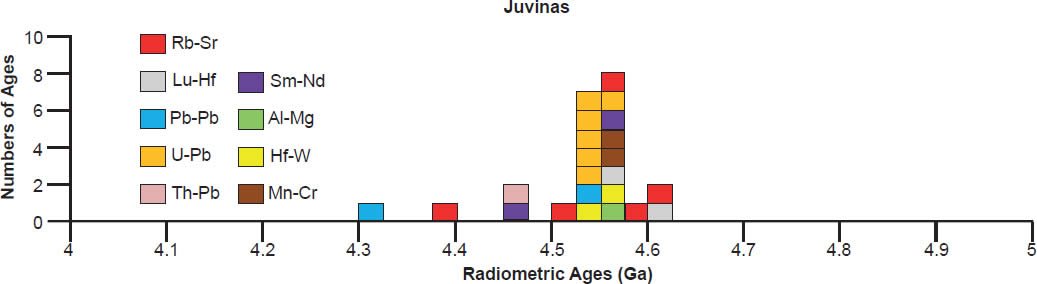
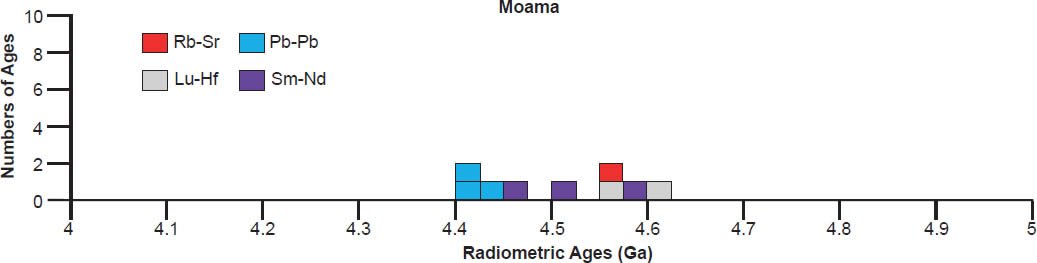
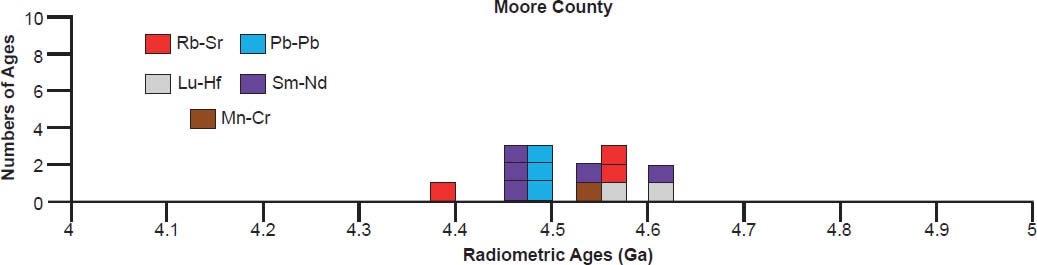
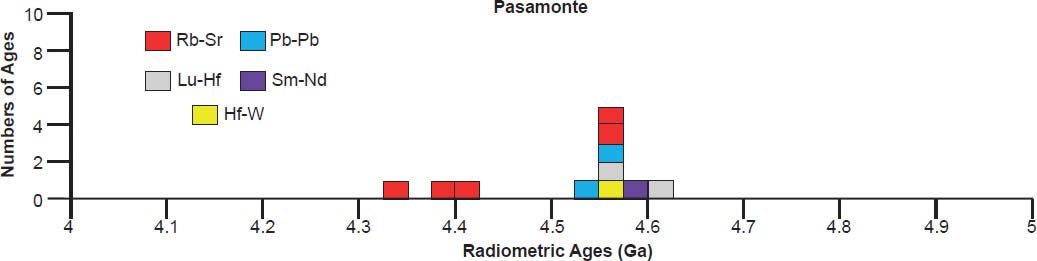
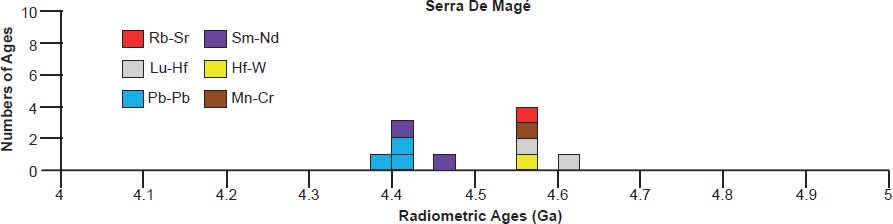
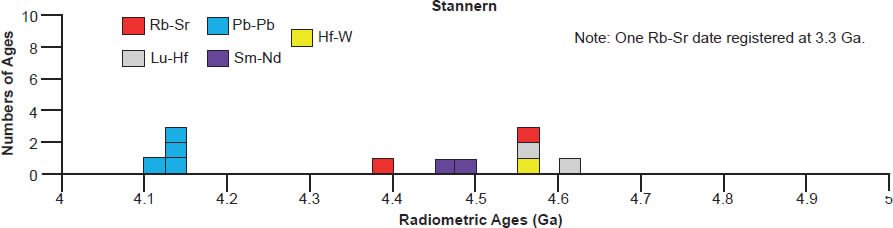
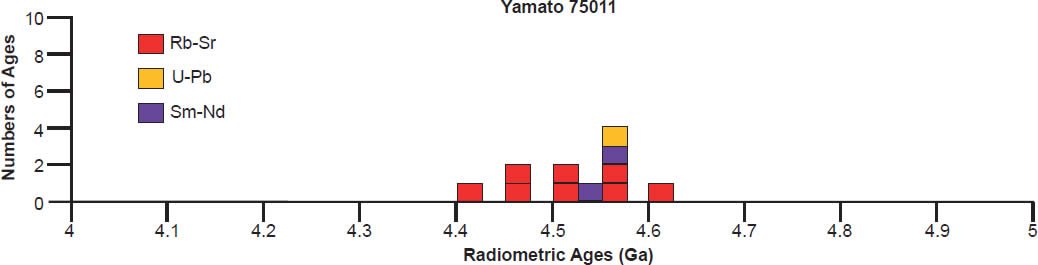
Fig. 6. Frequency versus radioisotope ages histogram diagram for the isochron ages for whole-rock samples and some or all components of 12 eucrite achondrites, with color coding being used to show the ages obtained by the different radioisotope dating methods.
An explanation for the agreement of ages
It has already been noted above that the Mn-Cr, Hf-W, Al-Mg, I-Xe, and Pu-Xe methods are calibrated directly or via intermediaries against the Pb-Pb ages yielded by other meteorites, which invariably guarantees the ages obtained by these methods will align with, or are adjusted to, the Pb-Pb ages that usually cluster around 4.55–4.57 Ga to date these eucrites. Indeed, as Snelling (2014a, b) found, the ages of most of the 28 meteorites investigated so far have been established directly by Pb-Pb ages or indirectly by Pb-Pb calibrated ages defining the clustering at 4.5–4.57 Ga.
Examination of the relevant literature reveals that the 87Rb decay rate has been determined by calibrating Rb-Sr dates against Pb-Pb dates on the same rock samples (Nebel, Scherer, and Mezger 2011; Snelling 2014c). Similarly, Snelling (2014d) has found that the 176Lu decay rate has also been determined by calibrating Lu-Hf dates against Pb-Pb dates on the same mineral samples from the same rocks (Söderlund et al. 2004). In other words, the Rb-Sr and Lu-Hf dates were adjusted to agree with the Pb-Pb ages, so it is hardly surprising when the adjusted decay constants are used to calculate the Rb-Sr and Lu-Hf dates yielded by other rocks and minerals, and here by these meteorites, they often agree with the meteorites’ 4.55–4.57 Ga Pb-Pb ages. It is also well known that the 40K decay constant has been calibrated against standard samples of known Pb-Pb ages (Renne et al. 2010), so ultimately all K-Ar and Ar-Ar dates are adjusted accordingly. Even the 147Sm decay constant has been calibrated against Pb-Pb ages on the same samples (Dickin 2005, pp. 70–71; Lugmair 1974; Lugmair, Scheinin, and Marti 1975).
Therefore, ultimately all other radioisotopic dating methods have been effectively calibrated against Pb-Pb ages on the same rocks and minerals, and in some cases on the same meteorites. These calibrations are simply done by determining the Rb-Sr or Lu-Hf ages for specific rocks, meteorites, or minerals whose Pb-Pb ages have also been determined. Then it is assumed that the Pb-Pb ages are the most accurate and true ages for those rocks, meteorites, or minerals. So if the Rb-Sr or Lu-Hf ages disagree with the Pb-Pb ages, then the 87Rb and 176Lu half-life values are adjusted so that all the ages agree. It is thus hardly surprising that often there is agreement between all the radioisotope dates yielded on the same rocks, minerals and meteorites, except where it is interpreted that other factors have disturbed the radioisotope systems which thus have yielded a plethora of different dates (see below). This ultimately means that all meteorite ages are dependent on the reliability of determinations of the 238U and 235U decay constants, and the critical 238U/235U ratio. Yet discrepancies and variations have now been found between the 238U/235U ratio in U-bearing earth-based (terrestrial) minerals and rocks and the 238U/235U ratio in meteorites (Brennecka and Wadhwa 2012; Hiess et al. 2012). It also may be significant that the estimated half-life of 238U is 4.468 Ga, which is almost identical to the claimed 4.55–4.57 Ga age of the earth, the asteroids, and the meteorites derived from them.
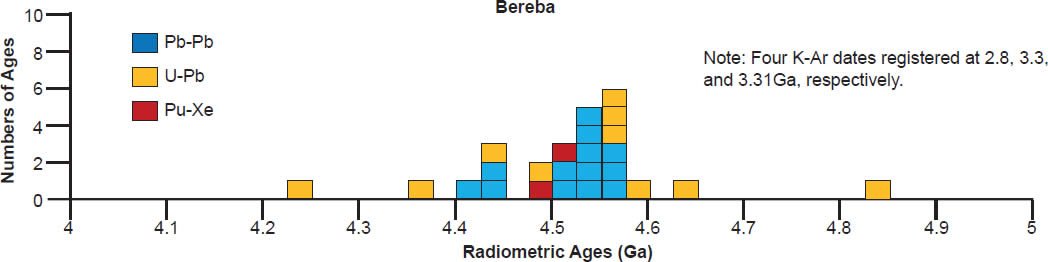
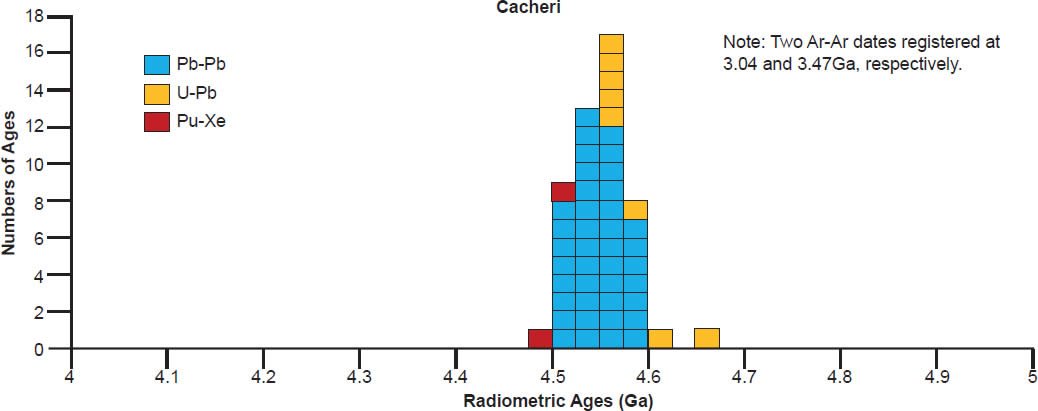
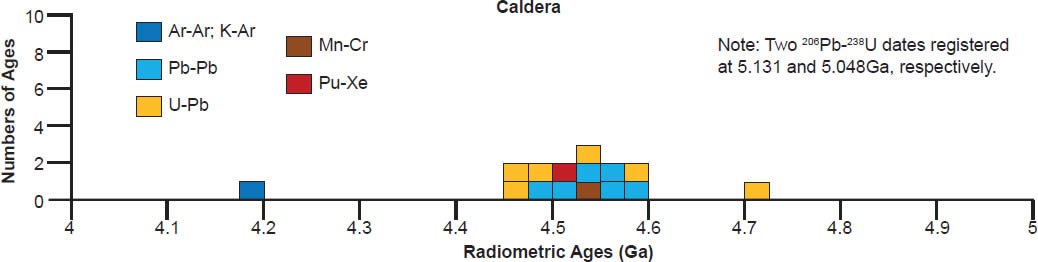
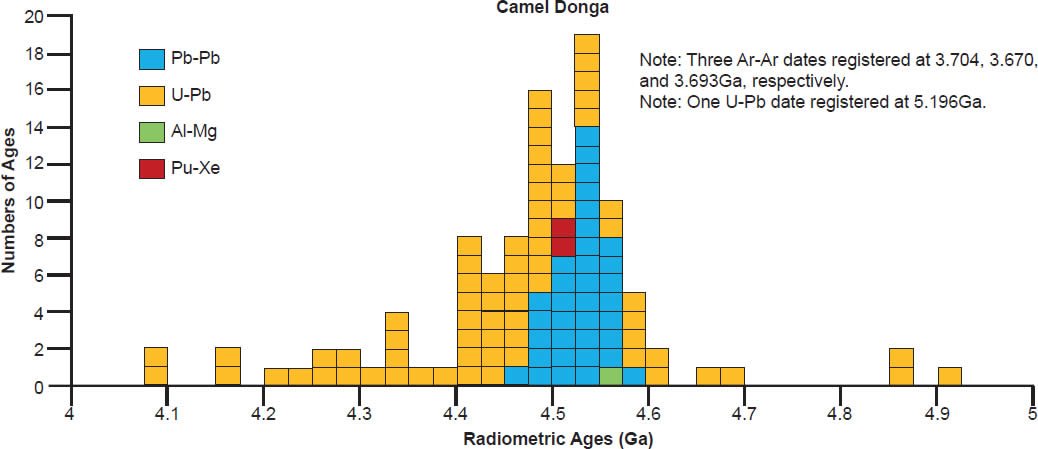
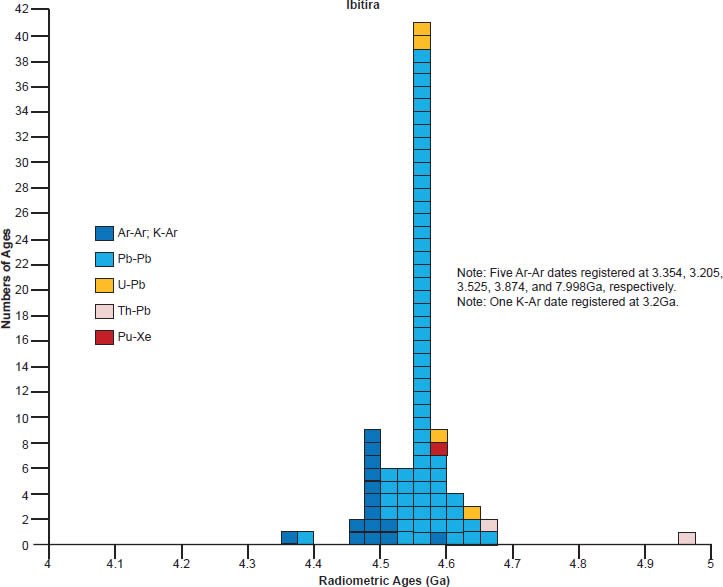
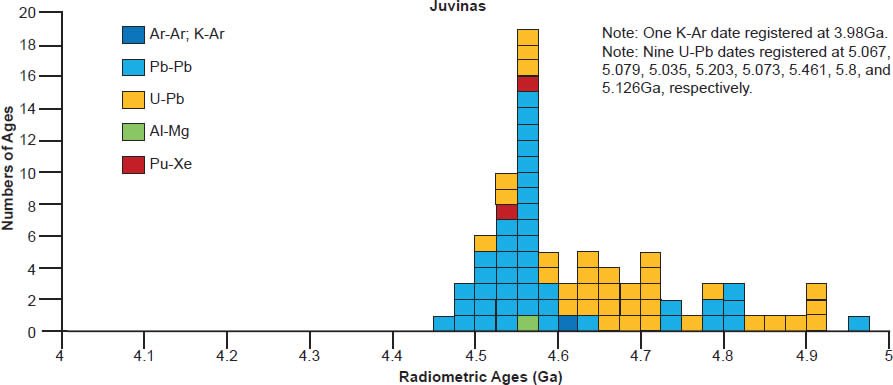
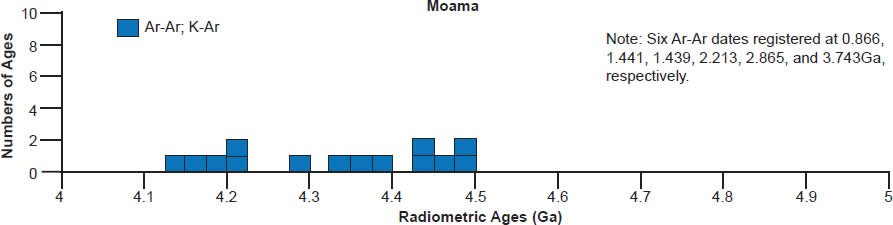
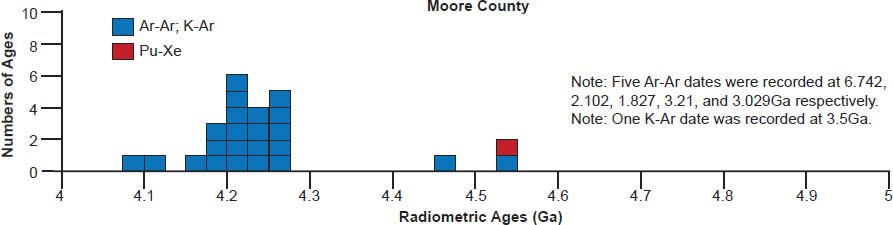
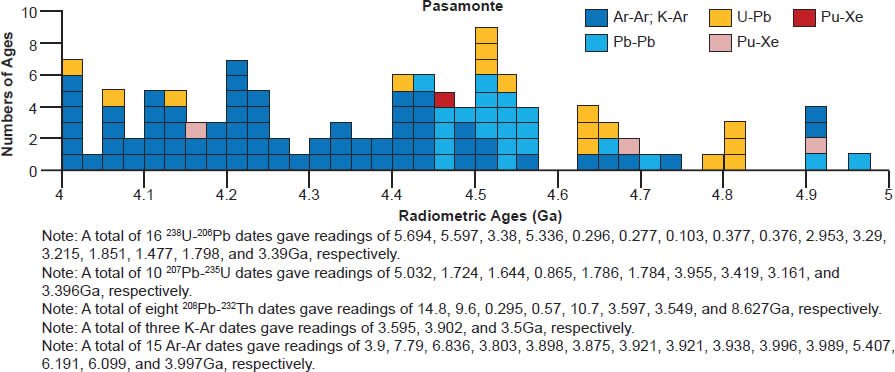
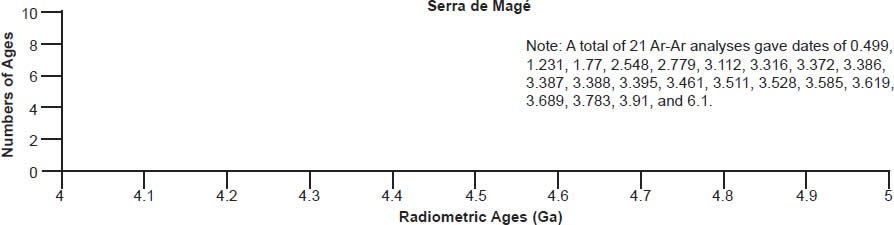
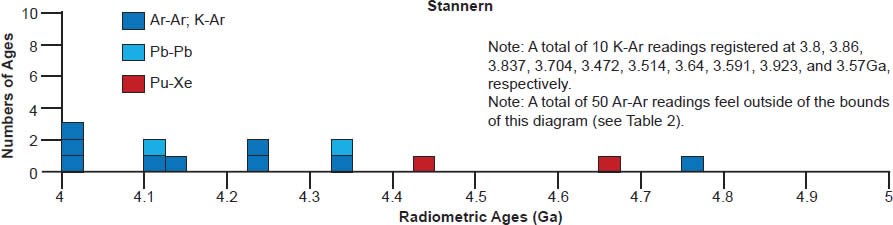
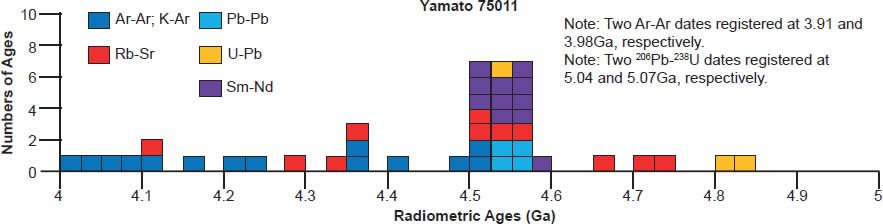
Fig. 7. Frequency versus radioisotope ages histogram diagram for the model ages for whole-rock samples and some or all components of 12 eucrite achondrites, with color coding being used to show the ages obtained by the different radioisotope dating methods.
Explanations for the scattering of ages
The usual explanation for such scattering of isochron and model ages is the thermal disturbance of the isotope systems subsequent to formation of the parent body from which the meteorites came, affecting either the parent body or subsequently the meteorites, or both (Bogard 2011; Lewis 1997; Trieloff et al. 2003). This must be especially the case where in this instance the scattering of ages is rife in the K-Ar, Ar-Ar, Rb-Sr, Sm-Nd, and U-Th-Pb systems. Confirmation of this explanation would seem to be provided by the fact that these eucrites (basaltic achondrites) are invariably metamorphosed, because it is well-documented that metamorphism resets these radioisotope systems (Faure and Mensing 2005; Snelling 2000).
However, not all these eucrites are metamorphosed, at least not to the same extent. Pasamonte (fig.5a) and Serra de Magé (fig. 5c) are regarded as least metamorphosed or unmetamorphosed, though in the latter the original igneous pyroxenes have exsolved augite lamellae as a result of some metamorphism. Yet in both meteorites their radioisotope systems have been greatly disturbed. For Pasamonte the Rb-Sr isochron ages are younger than the 4.55–4.57 Ga clustering and the K-Ar, Ar-Ar, and U-Th-Pb model ages are widely scattered and are both younger and older. Similarly for Serra de Magé the Sm-Nd and Pb-Pb isochron ages are younger than the 4.55–4.57 Ga clustering, whereas the Ar-Ar model ages are widely scattered and invariably grossly younger.
McSween et al. (2011), based on the work of Bogard and Garrison (1995, 2003, 2009) and Bogard (2011), suggest another explanation for the lower Ar-Ar model ages for many eucrites, such as for Cacheri, Caldera, Camel Donga, Ibitira, Juvinas, Moama, Moore County, Pasamonte, Serra de Magé, Stannern, and Yamato75011 in this study. Brecciated eucrites evidence significant Ar degassing, which reset their Ar-Ar ages to between 3.1–4.1 Ga. Since the timing of thermal and shock metamorphism is supposedly best determined from Ar-Ar ages, Bogard and Garrison (2009) argued that these young Ar-Ar ages represent impact cratering events on the surface of the parent asteroid 4-Vesta. They claimed that unbrecciated and unshocked eucrites have Ar-Ar ages near 4.5 Ga, whereas brecciated eucrites yield younger Ar-Ar ages that cluster on a probability plot in clusters at ~3.5, 3.8, 3.9, and 4.0 Ga (fig. 8). These they concluded were impact events that brecciated the eucrites and reset their Ar-Ar ages. However, in this study Ibitira, Moore County, Pasamonte, and Serra de Magé are all unbrecciated, as evidenced in thin sections (fig. 5), yet they yield many Ar-Ar ages younger than 4.5 Ga, some around 4.5 Ga, and quite a few well above 4.5 Ga.
Fig. 8 Probability plot of 40Ar-39Ar ages of unbrecciated and brecciated eucrites, based on the work of Bogard and Garrison (1995, 2003, 2009), after Bogard (2011) and McSween et al. (2011). The peaks are interpreted as representing major impact events on their parent asteroid 4-Vesta.
Nevertheless, thermal disturbances tend to reset the radioisotope systems so that the resultant ages are lower than their original ages (Lewis 1997), whereas for all these eucrites the radioisotope ages are both younger and older than the believed formation age of the parent body, determined as 4.55–4.57 Ga from the clustering of all the radioisotope systems at that age. So perhaps there might be an additional explanation for the scattering of both the isochron and model ages for all these eucrites (basaltic achondrites).
Internal layering in parent 4-Vesta
NASA’s Dawn spacecraft mission to 4-Vesta investigated the asteroid’s surface during 2011–2012 with a Visible and Infrared (VIR) Spectrometer for mineral identification and mapping, and a Gamma Ray and Neutron Detector (GRaND) for geochemical analysis and mapping (McSween et al. 2014). As a consequence new evidence was provided to strengthen considerably the connection of the HED meteorites to 4-Vesta (McSween et al. 2013, 2014). For example, high-resolution visible-near infrared spectra indicated pyroxene compositions and abundances like those of the HED meteorites, the mapped petrologic complexity (unlike the homogeneity of smaller asteroids) was consistent with the range of rock compositions among the HED meteorites, and geochemical measurements of the regolith were similar to the compositions of HED meteorites (and unlike those of other achondrite types). These results have further strengthened uniformitarians’ attempts to explain the natural formation of 4-Vesta in the context of all other bodies in the solar system, and how it was shaped or modified by subsequent processes to produce its current internal structure and its surface features.
Regarded as a leftover planetary building block, with an average diameter of 510 km (317 mi) and a mean density of 3456 kg/m3 (216 lbs/ft3), 4-Vesta was once called the smallest terrestrial planet (McSween et al. 2014). It is believed by uniformitarians to be an intact example of a large, differentiated protoplanet, like those claimed to be the building blocks of terrestrial planet accretion from the solar nebula, and based on analyses of the HED meteorites is postulated to have a basaltic upper crust (as represented by the noncumulate basaltic eucrites) that overlies a cumulate eucrite mid-crust layer and then a diogenite lower crust, with a depleted peridotitic (harzburgite) mantle beneath and then an iron core (Mandler and Elkins-Tanton 2013; Zuber et al. 2011). Petrological analyses of eucrites coupled with thermal evolution modeling has led to the proposal of two possible mechanisms of silicate-metal differentiation leading to the formation of the basaltic achondrites of Vesta’s crust—the earlier model of equilibrium partial melting (Stolper 1977), or the later now popular model of crystallization of residual liquids (eucrites) and cumulates (diogenites) from a postulated cooling magma ocean (Mandler and Elkins-Tanton 2013; Righter and Drake 1997). For a body the size of 4-Vesta it is postulated that subsequent eruptions directly to the surface via dikes would be mechanically very difficult, so instead, large magma chambers would likely have formed in the subsurface and flows of basaltic eucrites could have erupted episodically from these chambers. Geochemical trends in basaltic eucrites (the main group trend and the Stannern trend) would seem to require multiple magmas and complex processes within this asteroid’s crust (Barrat et al. 2007).
Thus a complex history for 4-Vesta has been elucidated by uniformitarians using the range of ages obtained for the HED meteorites yielded by the various radioisotope dating techniques. They even postulate that the differentiation of the crust and mantle occurred close to 4.56 Ga within 1–3 Myr of the formation of the solar system, as defined by the Pb-Pb isochron age of the CAIs in chondrites, along with core formation by silicate-metal fractionation at the same time or soon thereafter (McSween et al. 2011, 2014). The earliest magmatic activity supposedly occurred at ~5 Myr after formation of the solar system, and then persisted perhaps for as much as ~50–150 Myr. Then in common with other bodies in the solar system, in the period from 4.1 Ga to 3.5 Ga often called the “late heavy bombardment” 4-Vesta was evidently struck by careening, massive bolides, as deduced from the reset Ar-Ar ages (fig. 8).
A biblical perspective
Any such postulated history for the formation of the asteroid 4-Vesta, and of course for the solar system itself, is completely invalidated by the divinely provided biblical account of the six normal days of God creating during the Creation Week. On Day One God ex nihilo created the earth (Genesis 1:1), and only on Day Four did He make the sun and the moon to provide light on the earth during the day and night respectively (Genesis 1:14–16). We are not specifically told that the rest of the solar system was also created on Day Four, but He did make the stars also on that day, and lights were placed in the expanse of the heavens to be for signs and seasons. From this description it is not unreasonable to conclude that the rest of the solar system was made on Day Four, including the asteroids. Furthermore, each entity God created and made during these six normal days of the Creation Week was formed exceedingly rapidly within the time and space of each normal day, so by the end of Day Four asteroid 4-Vesta was a completely formed entity, with an iron core, ultramafic mantle, and basaltic crust, all the necessary silicate-metal fractionation and crust-mantle differentiation happening exceedingly rapidly within hours, and thus not requiring the millions of years postulated by uniformitarians.
Given the general consensus that the asteroids consist of leftover material from the formation of the solar system, Snelling (2014a, b) proposed that the accepted coincident 4.55–4.57 Ga ages for the earth and many meteorites could be due to the earth and the parent asteroids having been created by God from the same primordial material, which He had created on Day One, as already proposed by Faulkner (1999, 2013). The simplest unifying assumption would therefore be that all such primordial material may have had the same created isotopic endowment. This assumption seems to be borne out by the earth apparently having the same time-integrated Pb isotopic endowment and thus being the same Pb-Pb “age” as the meteorites plotted on the geochron (Patterson 1956). The earth’s current Pb isotopic endowment was represented on that geochron by the Pb isotopic composition of a modern oceanic sediment sample, which would appear to contain the time-integrated Pb isotopic endowment from the earth’s beginning which was then processed through the earth’s subsequent rock cycle (Tyler 1990). However, while the possibility that the created initial ratios of parent to daughter elements were different for the earth compared to those created for other solar system objects could be considered, that possibility seems unwarranted if God made all the solar system objects (planets, moons, and asteroids) from the same primordial material He had created on Day One, which is consistent with them all having a common Designer. Nevertheless, if there were created differences in the initial Pb isotopic ratios, then it should not have been possible to plot the meteorites and the earth on the same Pb-Pb geochron, or meteorites on the same Pb-Pb, U-Pb, Rb-Sr, Sm-Nd, Lu-Hf, and Re-Os isochrons (Snelling in prep.).
It would also seem reasonable to propose that God created some of all the isotopes at the beginning in the primordial material, including isotopes that subsequently also formed by radioisotope decay as daughter isotopes from parent isotopes, regardless of when radioisotope decay started. In other words, when God made the primordial material He included in it 206Pb, 207Pb, and 208Pb atoms along with 238U, 235U, and 232Th atoms. It is reasonable to posit that He did, given that when created the “primordial material” likely had to have some initial isotopic ratios. Even the conventional scientific community has assumed the initial material of the solar system had the “primeval” Pb isotopic ratios as measured in the troilite (iron sulfide) in the Canyon Diablo iron meteorite (Faure and Mensing 2005). This is consistent with God creating a fully-functioning universe, as typified by Him creating fruit trees already bearing fruit in fully-functioning soil on land, all during Day Three, and the sun, moon, asteroids, and stars fully-functioning in their ordained positions and roles on Day Four. Thus when by the end of Day Four the asteroid 4-Vesta had been formed, all the necessary silicate-metal fractionation and crust-mantle differentiation of that primordial material to produce its internal layering had happened exceedingly rapidly within hours. That silicate-metal fractionation and crust-mantle differentiation may have also resulted in some redistribution or mixing of parent and daughter atoms, the latter having been originally created rather than derived via radioactive decay. These processes may explain some of the scattering in the radioisotope ages for these eucrite meteorites, especially those older than the 4.55–4.57 Ga clustering.
At what point in time radioactive decay began is unclear from Scripture, and is still a matter of debate among creationists. The RATE project considered the possibility of a large amount of accelerated decay occurring during the Creation Week, as radioisotope decay was not regarded as decay in the sense of deterioration of matter (Vardiman, Snelling, and Chaffin 2005). It is instead a transmutation process, by which one element is changed into another. The daughter element is certainly not inferior to the parent element. However, it is the radiation given off which is harmful that causes concern as to whether the radioisotope decay processes meet the standard of God’s declaration of His completed creation being “very good” (Genesis 1:31).
In the context of the decay evident today due to the operation of the second law of thermodynamics, Anderson (2103) contended that there is no real biblical evidence to suggest that the second law was inoperable prior to the curse, and so argued that rather the second law was in effect from the beginning of creation. He thus also suggested that the tendency toward entropy implicit in the second law was never of a kind that conflicted with God’s declaration that the creation was “very good,” or that eventuated in the death of any sentient creature. On the other hand, it could be argued that radioisotope decay is more than the operation of the second law of thermodynamics; the additional outcome being the radiation produced which is harmful to life’s biological and chemical makeup. Indeed, if billions of years of accelerated radioisotope decay had occurred mainly during the early part of the Creation Week, as considered a possibility by the RATE team (Vardiman, Snelling, and Chaffin 2005), the enormous burst of radiation would surely have been detrimental to all life on the earth, for example, the plants of Day Three. It is for this reason that many creationists are not comfortable with postulating that accelerated radioisotope decay happened during the Creation Week, so maybe there was no radioisotope decay at all until it was started as part of the curse.
The lack of any evidence of a pattern of isochron ages in these 12 basaltic achondrite meteorites (eucrites), as well as in the 16 chondrite meteorites previously studied (Snelling 2014a, b), that matches the pattern found during the RATE project (Snelling 2005c; Vardiman, Snelling, and Chaffin 2005) would therefore strongly suggest that all these meteorites and their parent asteroids have not experienced any episode of accelerated radioisotope decay, either at the time of the creation of the primordial material on Day One or of their formation on Day Four, or since. This could then be taken to infer that no accelerated radioisotope decay occurred anywhere in the solar system during the Creation Week, including on the earth during Days One–Three. Such a conclusion is based on the assumption that the mechanism of small changes to the binding forces in the nuclei of the parent radioisotopes proposed as the cause of a past episode of accelerated radioisotope decay (Vardiman, Snelling, and Chaffin 2005) would thus have affected every atom making up the earth, and by logical extension every atom of the universe at the same time, because God appears to have created the physical laws governing the universe to operate consistently through time and space.
On the other hand, if this assumption is true, and it is consistent with God’s work of providentially maintaining the universe after He created it, then why is there evidence of an episode of accelerated radioisotope decay in the earth, but not in this asteroid and its meteorite fragments? The answer would seem to be that the accelerated radioisotope decay only occurred during the catastrophic global Flood event on the earth and that the asteroid 4-Vesta was not similarly affected. However, if the earth’s atoms were affected by accelerated radioisotope decay during the Flood, then surely every other atom in the universe would have been similarly affected. However, God is not bound by the physical laws He put in place at creation, as He can change them at any time anywhere or everywhere. After all, when Jesus Christ the Creator locally suspended the law of gravity as He walked on the stormy waters of the Sea of Galilee, the law of gravity was still operating at the same time to keep the disciples in their boat, their boat on the water and the earth in space in orbit around the sun. Thus God could have made small changes to the binding forces of the nuclei of only the earth’s atoms during the Flood to cause accelerated radioisotope decay only on the earth, while leaving the atoms making up the rest of the solar system and universe untouched. Perhaps the reason God initiated accelerated radioisotope decay only on the earth was to generate the heat necessary to initiate and drive the catastrophic plate tectonics which reshaped the earth’s surface during the Flood.
Another reason for arguing that accelerated radioisotope decay occurred in earth’s rocks only during the Flood is that the earth’s rocks contain the physical evidence of only 500–600 million years’ worth of radioisotope decay (as calculated using today’s measured decay rates), which equates to the same time period postulated by uniformitarians during which the geologic record of the Flood accumulated (Snelling 2009). This physical evidence of radioisotope decay in earth’s rocks is provided by radiohalos and fission tracks (Snelling 2005a, b). Each fully-formed U radiohalo, no matter where in the geologic record it occurs or the supposed age of its host rock, only represents up to 100 million years’ worth of U decay, so even if it is in a Precambrian (pre-Flood or Creation Week) granite it still only records up to 100 million or so years’ worth of U decay that occurred during the Flood, at the same time as new granites containing U radiohalos were forming in plutons which had intruded into fossil-bearing (and therefore Flood-deposited) sedimentary strata. On the other hand, up to 600 or so million years’ worth of fission tracks are found in zircon grains matching the radioisotope ages of those same zircon grains at the base of the strata record of the Flood (Snelling 2005b).
This still does not fully explain why there is such a spread of radioisotope “ages” from 4.03 Ga to the present in the earth’s rocks, or why the radioisotope “ages” of the oldest earth rock (the Acasta Gneiss, Canada) and the oldest mineral in an earth rock (a zircon grain in the Jack Hills sandstone, Western Australia) are 4.03 Ga and 4.4 Ga respectively rather than 4.56 Ga, the supposed age of the earth. The answer might be that the earth’s rocks, subsequent to their creation on Day One, first suffered from the processes of mixing of isotopes and re-setting of radioisotope “clocks” in the mantle and crust during the Day Three “Great Upheaval” when God formed the dry land, and then further suffered from mixing of isotopes and resetting of radioisotope “clocks” in the mantle and crust as a consequence of the catastrophic plate tectonics during the Flood, as well as the concurrent accelerated radioisotope decay.
By comparison, the Day Three “Great Upheaval” which the Scriptures describe as occurring on the earth could not have affected other bodies in the solar system, including the asteroid 4-Vesta which is the likely source of the meteorites in this study, because these other bodies were not created until Day Four. Thus we can be dogmatic that this event was earth-specific, as it was designed to produce the continental crust and the dry land on the earth in readiness for the subsequent creation of plants, birds, animals, and man. In any case, so far our observations of the surfaces of asteroids do not indicate any continental crust on them akin to that which formed on the earth on Day Three. However, when they were formed on Day Four their formation could have included incredibly rapid silicate-metal fractionation and mantle-crust differentiation with accompanying redistribution of the previously created parent and (what uniformitarians now interpret as) daughter isotopes.
The scatter in the radioisotope ages of the 28 meteorites studied thus far would then be due to processes subsequent to the initial creation of the parent asteroids from the primordial material on Day Four of the Creation Week that have reset the radioisotope “clocks” at various times, such as the initial fractionation and differentiation, heating due to impact cratering, impact disintegration and re-coalescing of the asteroids, space weathering, and heating on passage of the meteorites through the earth’s atmosphere (Bogard and Garrison 2009; Cloutis, Binzel and Gaffey 2014; Michel 2014; Norton 2002).
Where to from here?
As concluded by Snelling (2014a, b) from his studies of 16 chondrite meteorites, based on the assumptions made the 4.55–4.57 Ga radioisotope “ages” for the Bereba, Cacheri, Camel Donga, Ibitira, Juvinas, Pasamonte, Serra de Magé, and Yamato 75011 basaltic achondrite meteorites (eucrites) obtained primarily by Pb-Pb radioisotope isochron and model age dating of various constituent minerals and fractions (for example, Iizuka et al. 2014; Manhès, Allègre, and Provost 1984; Misawa, Yamaguchi, and Kaiden 2005; Tera, Carlson, and Boctor 1997; Zhou et al. 2013) are likely not their true real-time ages. The assumptions on which the radioisotope dating methods are based are simply unprovable, and in the light of the possibility of an inherited primordial geochemical signature, subsequent resetting of radioisotope “clocks” due to impact cratering of asteroids, and the evidence in earth rocks for past accelerated radioisotope decay, mixing of isotopes and resetting of radioisotope “clocks,” these assumptions are unreasonable.
However, we still need to develop a coherent and comprehensive explanation of what these radioisotope compositions in both meteorites and earth rocks really represent and mean within our biblical young-age creation-Flood framework for earth and universe history. We have some possible clues already, as discussed here, and a clearer picture may yet emerge from continued investigations now in progress. Examination of the radioisotope dating data for the remaining groups of achondrite meteorites is necessary to complete our understanding of what the meteorite radioisotope “ages” might mean. If only the earth was affected by accelerated radioisotope decay during the Flood, then it is also necessary to examine the radioisotope dating data for lunar rocks to determine whether the moon was affected by that aspect of the Flood catastrophe or not. Additionally, the radioisotope dating data for many more earth rocks from all levels of the geologic record need to be collated and examined. If accelerated radioisotope decay only occurred during the Flood, then it might be expected that the radioisotope “ages” of pre-Flood (mostly Precambrian) strata determined by the different methods would be noticeably discordant (Snelling 2005c), whereas the radioisotope “ages” of the strata formed during the Flood (mostly Phanerozoic) would be mostly concordant. This difference might be expected due to the pre-Flood rocks having already been formed and their radioisotope “clocks” started before the onset of the accelerated radioisotope decay during the Flood, when their radioisotope “clocks” would have been speeded up by different amounts according to the atomic weights of the parent radioisotopes. In contrast, the Flood rocks would have had their radioisotopes reset when those rocks formed and so their radioisotope “clocks” started only during the accelerated radioisotope decay of the Flood event. It may take the collation and examination of the huge radioisotope dating data sets of as many different earth rocks as possible from all levels of the geologic record to enable any firm conclusions to be made.
Whatever the radioisotope dating data for the earth’s rocks may reveal, it is already well-established that there are so many problems with the radioisotope dating methods which render them totally unreliable in providing time markers for the different stages in the earth’s history. Indeed, the investigations of determinations of the decay constants of each of the parent radioisotopes needs to be completed to provide further documentation of the uncertainties in that key time assumption. Therefore, even though most of these eucrites (basaltic achondrite meteorites) yield a consistent Pb-Pb isochron and model age of 4.55–4.57 Ga that cannot be their true real-time age, which according to the biblical paradigm is only about 6000 real-time years.
Conclusions
After decades of numerous careful radioisotope dating investigations of basaltic achondrite meteorites (eucrites) their Pb-Pb isochron and model age of 4.55–4.57 Ga has been well established. This date for these eucrites is supported for many of them by a strong clustering of their Pb-Pb isochron and model ages in the 4.55–4.57 Ga range, as well as being confirmed by both isochron and model age results via the U-Pb method, and to a lesser extent, by the Rb-Sr, Lu-Hf, and Sm-Nd methods. The Hf-W, Mn-Cr, Al-Mg, I-Xe, and Pu-Xe methods are all calibrated against the Pb-Pb isochron method, so their results are not objectively independent. Thus the Pb-Pb isochron dating method stands supreme in the conventional evolutionary uniformitarian community as the ultimate, most precise tool for determining the ages of the basaltic achondrite meteorites.
There are no discernible patterns in the isochron and model ages for these eucrites, apart from considerable scatter of the Rb-Sr, Sm-Nd, and some Pb-Pb isochron ages, and the considerable scatter of the K-Ar, Ar-Ar, Rb-Sr, U-Pb, Th-Pb, and even some Pb-Pb model ages. These basaltic achondrite ages do not follow the systematic pattern found in Precambrian rock units during the RATE project. The α-decay isochron ages are not always older than the β-decay isochron ages for particular eucrites, and among the β-decayers the isochron ages are not always older according to the increasing heaviness of the atomic weights of the parent radioisotopes, or the increasing lengths of their half-lives. Thus there appears to be no consistent evidence in these basaltic achondrite meteorites similar to the evidence found in earth rocks of past accelerated radioisotope decay.
Any explanation for the 4.55–4.57 Ga age for these basaltic achondrite meteorites needs to consider their origin. These meteorites are regarded as fragments of the asteroid 4-Vesta, debris derived from impact cratering of its surface and collisions with other asteroids. Even in the naturalistic paradigm the asteroids, and thus the meteorites, are regarded as “primordial material” left over from the formation of the solar system. Similarly, it has been suggested the Hebrew of the Genesis text allows for God to have made “primordial material” on Day One of the Creation Week from which He made the earth on Day One and the non-earth portion of the solar system on Day Four. Thus today’s measured radioisotope compositions of these eucrites may reflect a geochemical signature of that “primordial material,” which included atoms of all elemental isotopes created by God. Therefore if some, or perhaps most, of the daughter isotopes were thus “inherited” by these basaltic achondrite meteorites when they were formed from that “primordial material,” and the parent isotopes in the meteorites have only been subjected to some subsequent radioisotope decay (and none at accelerated rates), then the 4.55–4.57 Ga Pb-Pb isochron “age” for these eucrites cannot be their true real-time age, which according to the biblical paradigm is only about 6000 real-time years.
However, these conclusions and suggested explanations as discussed are still only tentative, their confirmation or adjustment awaiting the examination of more radioisotope dating data from meteorites in remaining groups. Furthermore, further extensive studies of the radioisotope dating of lunar rocks and rocks from all levels of the earth’s geologic record are required to attempt to systematize what proportions of the isotopes in each radioisotope dating system measured today are due to inheritance from the “primordial material,” past accelerated radioisotope decay, and mixing, additions, and subtractions in the earth’s mantle and crust through earth history, particularly during the Day Three Upheaval and then subsequently during the Flood.
Acknowledgments
The invaluable help of my research assistant in compiling these radioisotope dating data into the tables and then plotting the data in the color coded age versus frequency histogram diagrams is acknowledged. Also, our production assistant Laurel Hemmings is especially thanked for her painstaking work in preparing these papers for publication.
References
Allègre, C. J., J.-L. Birck, S. Fourcade, and M. P. Semet. 1975. Rubidium-87/strontium-87 age of Juvinas basaltic achondrite and early igneous activity in the solar system. Science 187, no. 4175:436–438.
Amelin, Y., A. N. Krot, I. D. Hutcheon, and A. A. Ulyanov. 2002. Lead isotopic ages of chondrules and calcium-aluminum-rich inclusions. Science 297, no. 5587:1678–1683.
Amelin, Y., M. Wadhwa, and G.W. Lugmair. 2006. Pb- isotopic dating of meteorites using 202Pb-205Pb double spike: Comparison with other high-resolution chronometers. Lunar and Planetary Science Conference 37: #1970.
Amelin, Y. A., A. Kaltenbach, T. Iizuka, C. H. Stirling, T. R. Ireland, M. Petaev, and S. B. Jacobsen. 2010. U-Pb chronology of the Solar System’s oldest solids with variable 238U/235U. Earth and Planetary Science Letters 300, no. 3–4:343–350.
Anderson, L. A. Jr. 2013. Thoughts on the goodness of creation: In what sense was creation “perfect”? Answers Research Journal 6:391–397. https://answersingenesis.org/physics/thoughts-on-the-goodness-of-creation-in-what-sense-was- creation-perfect/.
Bansal, B.M., C.-Y. Shih, and H. Wiesmann. 1985. Rb-Sr internal isochron age of a subophitic basalt clast from the Y75011 eucrite. Lunar and Planetary Science Conference 16:25–26.
Barrat, J. A., A. Yamaguchi, R. C. Greenwood, M. Bohn, J. Cotten, M. Benoit, and I. A. Franchi. 2007. The Stannern trend eucrites: Contamination of main group eucritic magmas by crustal partial melts. Geochimica et Cosmochimica Acta 71, no. 16:4108–4124.
Basaltic Volcanism Study Project. 1981. Basaltic volcanism on the terrestrial planets. New York, New York: Pergamon Press, Inc.
Binzel, R.P., and S. Xu. 1993. Chips off of asteroid Vesta: Evidence for the parent body of basaltic achondrite meteorites. Science 260, no. 5105:186–191.
Birck, J.-L., and C.J. Allègre. 1978. Chronology and chemical history of the parent body of basaltic achondrites studied by the 87Rb-87Sr method. Earth and Planetary Science Letters 39, no. 1:37–51.
Blichort-Toft, J., M. Boyet, P. Télouk, and F. Albarède. 2002. 147Sm-143Nd and 176Lu-176Hf in eucrites and the differentiation of the HED parent body. Earth and Planetary Science Letters 204, no. 1–2:167–181.
Bogard, D. D., G. J. Taylor, K. Keil, M. R. Smith, and R. A. Schmitt. 1985. Impact melting of the Cachari eucrite 3.0 Gy ago. Geochimica et Cosmochimica Acta 49, no. 4:941–946.
Bogard, D. D., and D. H. Garrison. 1995. 39Ar-40Ar age of the Ibitira eucrite and constraints on the time of pyroxene equilibration. Geochimica et Cosmochimica Acta 59, no. 20:4317–4322.
Bogard, D. D., and D. H. Garrison. 2003. 39Ar-40Ar ages of eucrites and thermal history of asteroid 4 Vesta. Meteoritics and Planetary Science 38, no. 5:669–710.
Bogard, D. D., and D. H. Garrison. 2009. Ar-Ar impact heating ages of eucrites and timing of the LHB. Lunar and Planetary Science Conference 40: #1131.
Bogard, D.D. 2011. K-Ar ages of meteorites: Clues to parent- body thermal histories. Chemie der Erde 71, no. 3:207–226.
Boyet, M., R.W. Carlson, and M. Horan. 2010. Old Sm-Nd ages for cumulate eucrites and redetermination of the solar system initial 146Sm/144Sm ratio. Earth and Planetary Science Letters 291, no. 1–4:173–181.
Brazzle, R. H., O. V. Pravdivtseva, A. P. Meshik, and C. M. Hohenberg. 1999. Verification and interpretation of the I-Xe chronometer. Geochimica et Cosmochimica Acta 63, no. 5:739–760.
Brennecka, G.A., and M. Wadhwa. 2012. Uranium isotope compositions of the basaltic angrite meteorites and the chronological implications for the early Solar System. Proceedings of the National Academy of Sciences USA 109, no. 24:9299–9303.
Bukovanska, M., and T.R. Ireland. 1993. Zircons in eucrites: Pristine and disturbed U–Pb systematics. Meteoritics 28, no. 3:333.
Carlson, R. W., F. Tera, and N. Z. Boctor. 1988. Radiometric geochronology of the eucrites Nuevo Laredo and Bereba. Lunar and Planetary Science Conference 19:166–167.
Chen, J. H., and G. J. Wasserburg. 1985. U-Th-Pb isotopic studies of meteorite ALHA 81005 and Ibitira. Lunar and Planetary Science Conference 16:119–120.
Claydon, J. L., S. A. Crowther, and J. D. Gilmour. 2012. Xenon in the anomalous eucrites Bunburra Rockhole and Ibitira. Lunar and Planetary Science Conference 43:#1884.
Claydon, J. L., S. A. Crowther, and J. D. Gilmour. 2013. The I-Pu-Xe system in anomalous and Vestian eucrites: Was Vesta unusually large? Lunar and Planetary Science Conference 44:#2173.
Clayton, R. N., and T. K. Mayeda. 1996. Oxygen-isotope studies of achondrites. Geochimica et Cosmochimica Acta 60, no. 11:1999–2018.
Cloutis, E. A., R. P. Binzel, and M. J. Gaffey. 2014. Establishing asteroid-meteorite links. Elements 10, no. 1:25–30.
Consolmagno, G. J., and M. J. Drake. 1977. Composition and evolution of the eucrite parent body: Evidence from rare earth elements. Geochimica et Cosmochimica Acta 41, no. 9:1271–1282.
Cumming, G.L. 1969. A recalculation of the age of the solar system. Canadian Journal of Earth Sciences 6, no. 4:719–735.
Dalrymple, G. B. 1991. The age of the earth. Stanford, California: Stanford University Press.
Dalrymple, G.B. 2004. Ancient earth, ancient skies. Stanford, California: Stanford University Press.
Dickin, A. P. 2005. Radiogenic isotope geology. 2nd ed. Cambridge, United Kingdom: Cambridge University Press.
Drake, M.J. 2001. The eucrite/Vesta story. Meteoritics and Planetary Science 36, no. 4:501–513.
Faulkner, D.R. 1999. A biblically-based cratering theory. Creation Ex Nihilo Technical Journal 13, no. 1:100–104.
Faulkner, D.R. 2013. A proposal for a new solution to the light travel time problem. Answers Research Journal 6:295–300. https://answersingenesis.org/astronomy/starlight/a-proposal-for-a-new-solution-to-the-light-travel-time-problem/
Faure, G., and T.M. Mensing. 2005. Isotopes: Principles and applications. 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Galer, S. J. G., and G. W. Lugmair. 1996. Lead isotope systematics of noncumulate eucrites. Meteoritics and Planetary Science 31:A47–A48.
Garrison, D. H., and D. D. Bogard. 1995. 39Ar-40Ar age of Ibitira: Dating the time of chemical equilibration of eucritic pyroxenes? Lunar and Planetary Science Conference 26:443–444.
Göpel, C., G. Manhès, and C.-J. Allègre. 1992. U-Pb study of the Acapulco meteorite. Meteoritics 27, no. 3:226.
Göpel, C., G. Manhès, and C.-J. Allègre. 1994. U-Pb systematics of phosphates from equilibrated ordinary chondrites. Earth and Planetary Science Letters 121, no. 1–2:153–171.
Hamet, J., N. Nakamura, D. M. Unruh, and M. Tatsumoto. 1978. Origin and history of the cumulate eucrite Moama as inferred from REE abundances, Sm-Nd and U-Pb systematics. Proceedings of the Lunar and Planetary Science Conference 9:1115–1136.
Hampel, W., H. Wänke, H. Hofmeister, B. Spettel, and G. F. Herzog. 1980. 26Al and rare gases in Allende, Bereba and Juvinas: Implications for production rates. Geochimica et Cosmochimica Acta 44, no. 3:539–547.
Hans, U., T. Kleine, and B. Bourdon. 2013. Rb-Sr chronology of volatile depletion in differentiated protoplanets: BABI, ADOR and ALL revisited. Earth and Planetary Science Letters 374:204–214.
Hiess, J., D. J. Condon, N. McLean, and S. R. Noble. 2012. 238U/235U systematics in terrestrial uranium-bearing minerals. Science 335, no. 6076:1610–1614.
Heymann, D., E. Mazor, and E. Anders. 1968. Ages of calcium- rich achondrites – I. Eucrites. Geochimica et Cosmochimica Acta 32, no. 12:1241–1268.
Iizuka, T., A. Kaltenbach, Y. Amelin, C.H. Stirling, and A. Yamaguchi. 2013. U-Pb isotope systematics of eucrites in relation to their thermal history. Lunar and Planetary Science Conference 44:#1907.
Iizuka, T., Y. Amelin, A. Kaltenbach, P. Koefoed, and C.H. Stirling. 2014. U-Pb systematics of the unique achondrite Ibitira: Precise age determination and petrogenetic implications. Geochimica et Cosmochimica Acta 132:259–273.
Jacobsen, S. B. and G. J. Wasserburg. 1984. Sm-Nd isotopic evolution of chondrites and achondrites, II. Earth and Planetary Science Letters 67, no. 2:137–150.
Jacobsen, B., Q.-Z. Yin, F. Moynier, Y. Amelin, A. N. Krot, K. Nagashima, I. D. Hutcheon, and H. Palme. 2008. 26Al-26Mg and 207Pb-206Pb systematics of Allende CAIs: Canonical solar initial 26Al/27Al ratio reinstated. Earth and Planetary Science Letters 272, no. 1–2:353–364.
Kennedy, T., F. Jourdan, A. W. R. Bevan, M. A. M. Gee, and A. Frew. 2013. Impact history of the HED parent body(ies) clarified by new 40Ar/39Ar analyses of four HED meteorites and one anomalous basaltic achondrite. Geochimica et Cosmochimica Acta 115:162–182.
Kleine, T., C. Münker, K. Mezger, and H. Palme. 2002. Rapid accretion and early core formation on asteroids and the terrestrial planets from Hf-W chronometry. Nature 418:952–955.
Kleine, T., K. Mezger, C. Münker, H. Palme, and A. Bischoff. 2004. 182Hf-182W isotope systematics of chondrites, eucrites, and martian meteorites: Chronology of core formation and early mantle differentiation in Vesta and Mars. Geochimica et Cosmochimica Acta 68, no. 1:2935–2946.
Kleine, T., K. Mezger, H. Palme, E. Scherer, and C. Münker. 2005. The W isotope composition of eucrite metals: constraints on the timing and cause of the thermal metamorphism of basaltic eucrites. Earth and Planetary Science Letters 231, no. 1–2:41–52.
Krot, A. N., K. Keil, C. A. Goodrich, E. R. D. Scott, and M. K. Weisberg. 2005. Classification of meteorites. In Meteorites, Comets, and Planets, ed. A. M. Davis, Treatise on Geochemistry, vol. 1, 83–128. Amsterdam, Netherlands: Elsevier.
Kunz, J., M. Trieloff, K. D. Bobe, K. Metzler, D. Stöffler, and E. K. Jessberger. 1995. The collisional history of the HED parent body inferred from 40Ar-39Ar ages of eucrites. Planetary and Space Science 43, no. 3:527–543.
Lee, S. R., H. Kim, D.-L. Cho, H. Kenji, and H. Hidaka. 2009. U-Pb dating of zircons from eucrites: A preliminary report. Geochimica et Cosmochimica Acta 73:A737.
Lewis, J.S. 1997. Physics and chemistry of the solar system. Rev. ed. London, England: Academic Press.
Lugmair, G.W. 1974. Sm-Nd ages: A new dating method. Meteoritics 9, no. 4:369.
Lugmair, G. W., and N. B. Scheinin. 1975. Sm-Nd systematics of the Stannern meteorite. Meteoritics 10, no. 4:447–448.
Lugmair, G. W., N. B. Scheinin, and K. Marti. 1975. Search of extinct 146Sm, 1. The isotopic abundance of 142Nd in the Juvinas meteorite. Earth and Planetary Science Letters 27, no. 1:79–84.
Lugmair, G. W., and K. Marti. 1977. Sm-Nd-Pu timepieces in the Angra dos Reis meteorite. Earth and Planetary Science Letters 35, no. 2:273–284.
Lugmair, G. W., N. B. Scheinin, and R. W. Carlson. 1977. Sm- Nd systematics of the Serra de Mage eucrite. Meteoritics 12, no. 3:300–301.
Lugmair, G. W., and S. J. G. Galer. 1992. Age and isotopic relationships among the angrites Lewis Cliff 86010 and Angra dos Reis. Geochimica et Cosmochimica Acta 56, no. 4:1673–1694.
Lugmair, G. W., and A. Shukolyukov. 1998. Early solar system timescales according to 53Mn-53Cr systematics. Geochimica et Cosmochimica Acta 62, no. 16:2863–2886.
Mandler, B. E., and L. T. Elkins-Tanton. 2013. The origin of eucrites, diogenites, and olivine diogenites: Magma ocean crystallization and shallow magma chamber processes on Vesta. Meteoritics and Planetary Science 48, no. 11:2333–2349.
Manhès, G., and C. J. Allègre 1980. U-Th-Pb systematics of the Juvinas achondrite. Meteoritics 15, no. 4:329.
Manhès, G., C. J. Allègre, and A. Provost. 1984. U-Th-Pb systematics of the eucrite “Juvinas”: Precise age determination and evidence for exotic lead. Geochimica et Cosmochimica Acta 48, no. 11:2247–2264.
Manhès, G., M. Tatsumoto, D. M. Unruh, J.-L. Birck, and C. J. Allègre. 1975. Comparative 238U-206Pb, 235U-207Pb, 232Th-208Pb, 206Pb-207Pb and 87Rb-87Sr ages of basaltic achondrites and early evolution of the solar system. Lunar Science VI:546–547.
Manhès, G., C. Göpel, and C. J. Allègre. 1987. High resolution chronology of the early solar system based on lead isotopes. Meteoritics 22:453–454.
McCord, T. B., J. B. Adams, and T. V. Johnson. 1970. Asteroid Vesta: Spectral reflectivity and compositional implications. Science 168, no.3938:1445–1447.
McSween, H. Y. Jr., D. W. Mittlefehldt, A. W. Beck, R. G. Mayne, and T. J. McCoy. 2011. HED meteorites and their relationship to the geology of Vesta and the Dawn mission. Space Science Reviews 163, no. 1–4:141–174.
McSween, H. Y. Jr., R. P. Binzel, M. C. De Sanctis, E. Ammannito, T. H. Prettyman, A. W. Beck, V. Reddy et al. 2013. Dawn; the Vesta-HED connection; and the geologic context for eucrites, diogenites, and howardites. Meteoritics and Planetary Science 48, no. 11:2090–2104.
McSween, H. Y. Jr., M. C. De Sanctis, T. H. Prettyman, and the Dawn Science Team. 2014. Unique, antique Vesta. Elements 10, no. 1:39–44.
Michel, P. 2014. Formation and physical properties of asteroids. Elements 10, no. 1:19–24.
Misawa, K., A. Yamaguchi, and H. Kaiden. 2005. U-Pb and 207Pb-206Pb ages of zircons from basaltic eucrites: Implications for early basaltic volcanism on the eucrite parent body. Geochimica et Cosmochimica Acta 69, no. 24:5847–5861.
Mittlefehldt, D. W. 2005. Achondrites. In Meteorites, comets, and planets, ed. A.M. Davis, Treatise on geochemistry, vol.1, 291–324. Amsterdam, The Netherlands: Elsevier.
Mittlefehldt, D. W., T. J. McCoy, C. A. Goodrich, and A. Kracher. 1998. Non-chondritic meteorites from asteroidal bodies. In Planetary materials, ed. J. J. Papike, Reviews in mineralogy, vol. 36, 4-1–4-195. Washington, DC: Mineralogical Society of America.
Miura, Y. N., K. Nagao, and T. Fujitani. 1993. 81Kr terrestrial ages and grouping of Yamato eucrites based on noble gas and chemical compositions. Geochimica et Cosmochimica Acta 57, no. 8:1857–1866.
Miura, Y. N., K. Nagao, N. Sugiura, T. Fujitani, and P. H. Warren. 1998. Noble gases, 81Kr-Kr exposure ages and 244Pu-Xe ages of six eucrites, Bereba, Binda, Camel Donga, Juvinas, Millbillillie, and Stannern. Geochimica et Cosmochimica Acta 62, no. 13:2369–2387.
Morris, J. D. 2007. The young earth. Rev. ed., pp. 59–61. Green Forest, Arkansas: Master Books.
Nebel, O., E. E. Scherer, and K. Mezger. 2011. Evaluation of the 87Rb decay constant by age comparison against the U-Pb system. Earth and Planetary Science Letters 301, no. 1–2:1–8.
Nichols R. H., C. M. Hohenberg, K. Kehm, Y. Kim, and K. Marti. 1994. I-Xe studies of the Acapulco meteorite: Absolute I-Xe ages of individual phosphate grains and the Bjurböle standard. Geochimica et Cosmochimica Acta 58, no. 11:2553–2561.
Norton, O. R. 2002. The cambridge encyclopedia of meteorites. Cambridge, United Kingdom: Cambridge University Press.
Nyquist, L. E., H. Takeda, B. M. Bansal, C.-Y. Shih, H. Wiesmann, and J. L. Wooden. 1986. Rb-Sr and Sm-Nd internal isochron ages of a subophitic basalt clast and a matrix sample from the Y75011 eucrite. Journal of Geophysical Research 91, no. B8:8137–8150.
Nyquist, L. E., Y. D. Reese, H. Wiesmann, and C.-Y. Shih. 1999. Two ages for Ibitira: A record of crystallization and recrystallization? Meteoritics and Planetary Science 34:A87–A88.
Papanastassiou, D. A., and G. J. Wasserburg. 1969. Initial strontium isotopic abundances and the resolution of small time differences in the formation of planetary objects. Earth and Planetary Science Letters 5:361–376.
Patchett, P. J., and M. Tatsumoto. 1980. Lu-Hf total-rock isochron for the eucrite meteorites. Nature 288:571–574.
Patterson, C. 1956. Age of meteorites and the earth. Geochimica et Cosmochimica Acta 10, no. 4:230–237.
Podosek, F. A., and J. C. Huneke. 1973. Argon 40-argon 39 chronology of four calcium-rich achondrites. Geochimica et Cosmochimica Acta 37, no. 3:667–684.
Prinzhofer, A., D. A. Papanastassiou, and G. J. Wasserburg. 1992. Samarium-neodymium evolution of meteorites. Geochimica et Cosmochimica Acta 56, no. 2:797–815.
Quitté, G., J.-L. Birck, and C. J. Allègre. 2000. 182Hf-182W systematics in eucrites: The puzzle of iron segregation in the early solar system. Earth and Planetary Science Letters 184, no.1:83–94.
Renne, P. R., R. Mundil, G. Balco, K. Min, and K. R. Ludwig. 2010. Joint determination of 40K decay constants and 40Ar*/40K for the Fish Canyon sanidine standard, and improved accuracy for 40Ar/39Ar geochronology. Geochimica et Cosmochimica Acta 74, no. 18:5349–5367.
Righter, K., and M. J. Drake. 1997. A magma ocean on Vesta: Core formation and petrogenesis of eucrites and diogenites. Meteoritics and Planetary Science 32, no. 6:929–944.
Schiller, M., J. A. Baker, and M. Bizzarro. 2010. 26Al-26Mg dating of asteroidal magmatism in the young solar system. Geochimica et Cosmochimica Acta 74, no. 16:4844–4864.
Shields, R. M., W. H. Pinson, and P. M. Hurley. 1965. The Rb87-Sr87 age of stony meteorites. Massachusetts Institute of Technology 13th Annual Program Report, pp.121–144.
Shukolyukov, A., and F. Begemann. 1996a. Pu-Xe dating of eucrites. Geochimica et Cosmochimica Acta 60, no. 13:2453– 2471.
Shukolyukov, A., and F. Begemann. 1996b. Cosmogenic and fissiogenic noble gases and 81Kr-Kr exposure age clusters of eucrites. Meteoritics and Planetary Science 31, no. 1:61–72.
Snelling, A. A. 2000. Geochemical processes in the mantle and crust. In Radioisotopes and the age of the earth: A young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, 123–304. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Snelling, A. A. 2005a. Radiohalos in granites: Evidence of accelerated nuclear decay. In Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, 101–207. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/radiohalos-granites-evidence-for-accelerated/.
Snelling, A. A. 2005b. Fission tracks in zircons: Evidence for abundant nuclear decay. In Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, 209–324. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http:// www.icr.org/article/fission-tracks-zircons-evidence-for/.
Snelling, A. A. 2005c. Isochron discordances and the role of inheritance and mixing of radioisotopes in the mantle and crust. In Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, 393–524. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr. org/article/isochron-discordances-role-inheritance/.
Snelling, A. A. 2009. Earth’s catastrophic past: creation and the Flood. Dallas, Texas: Institute for Creation Research.
Snelling, A. A. 2014a. Radioisotope dating of meteorites: I. The Allende CV3 carbonaceous chondrite. Answers Research Journal 7:103–145. https://answersingenesis.org/astronomy/age-of-the-universe/radioisotope-dating-meteorites-i-allende-cv3-carbonaceous-chrondrite/.
Snelling, A. A. 2014b. Radioisotope dating of meteorites: II. The ordinary and enstatite chondrites. Answers Research Journal 7:239–296. https://answersingenesis.org/astronomy/age-of-the-universe/radioisotope-dating-meteorites-i-allende-cv3-carbonaceous-chrondrite/.
Snelling, A. A. 2014c. Determination of the radioisotope decay constants and half-lives: Rubidium-87 (87Rb). Answers Research Journal 7:311–322. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rubidium-87-87rb/.
Snelling, A. A. 2014d. Determination of the radioisotope decay constants and half-lives: Lutetium-176 (176Lu). Answers Research Journal 7:483–497. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-lutetium-176/.
Snelling, A. A. n.d. Radioisotope dating of meteorites. V: Isochron ages of groups of meteorites. Answers Research Journal (in preparation).
Söderlund, U., P. J. Patchett, J. D. Vervoort, and C. E. Isachsen. 2004. The 176Lu decay constant determined by Lu-Hf and U-Pb isotope systematics of Precambrian mafic intrusions. Earth and Planetary Science Letters 219, no. 3–4:311–324.
Stolper, E. M. 1977. Experimental petrology of eucritic meteorites. Geochimica et Cosmochimica Acta 41:587–681.
Takeda, H. 1997. Mineralogical records of early planetary processes on the howardite, eucrite, diogenite parent body with reference to Vesta. Meteoritics and Planetary Science 32:841–853.
Takeda, H., H. Mori, and D. D. Bogard. 1994. Mineralogy and 39Ar-40Ar age of an old pristine basalt: Thermal history of the HED parent body. Earth and Planetary Science Letters 122, no. 1–2:183–194.
Tatsumoto, M., and D. M. Unruh. 1975. Formation and early brecciation of the Juvinas achondrite inferred from U-Th-Pb systematics. Meteoritics 10:500–501.
Tatsumoto, M., D. M. Unruh, and G. A. Desborough. 1976. U-Th-Pb and Rb-Sr systematics of Allende and U-Th-Pb of Orgueil. Geochimica et Cosmochimica Acta 40:617–634.
Tera, F., R. W. Carlson, and N. Z. Boctor. 1987. Isotopic and petrologic investigation of the eucrites Cacheri, Moore County and Stannern. Lunar and Planetary Science Conference 18:1004–1005.
Tera, F., R. W. Carlson, and N. Z. Boctor. 1997. Radiometric ages of basaltic achondrites and their relation to the early history of the solar system. Geochimica et Cosmochimica Acta 61, no.8:1713–1731.
Trieloff, M., E. K. Jessberger, I. Herrwerth, J. Hopp, C. Flénl, M. Ghélls, M. Bourot-Denise, and P. Pellas. 2003. Structure and thermal history of the H-chondrite parent asteroid revealed by thermochronometry. Nature 422:502–506.
Tyler, D.J. 1990. The tectonically-controlled rock cycle. In Proceedings of the Second International Conference on Creationism, ed. R. E. Walsh and C. L Brooks, Vol. 2, 293–301. Pittsburgh, Pennsylvania: Creation Science Fellowship.
Unruh, D. M., N. Nakamura, and M. Tatsumoto. 1977. History of the Pasamonte achondrite: Relative susceptibility of the Sm-Nd, Rb-Sr, and U-Pb systems to metamorphic events. Earth and Planetary Science Letters 37, no.1:1–12.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2005. Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/rate2/.
Wadhwa, M., and G. W. Lugmair. 1996. Age of the eucrite “Caldera” from convergence of long-lived and short-lived chronometers. Geochimica et Cosmochimica Acta 60, no. 23:4889–4893.
Wadhwa, M., C. N. Foley, P. E. Janney, and L. Spivak-Birndorf. 2004. Mg isotope systematics in eucrites: Implications for the 26Al-26Mg chronometer. Lunar and Planetary Science Conference 35:#1843.
Wasserburg, G. J., F. Tera, D. A. Papanastassiou, and J. C. Huneke. 1977. Isotopic and chemical investigations on Angra dos Reis. Earth and Planetary Science Letters 35, no. 2:294–316.
Weisberg, M. K., T. J. McCoy, and A. N. Krot. 2006. Systematics and evaluation of meteorite classification. In Meteorites and the early solar system II, ed. D.S. Lauretta and H.Y. McSween Jr., 19–52. Tucson, Arizona: University of Arizona Press.
Yamaguchi, A., G. J. Geoffrey, K. Keil, C. Floss, G. Crozaz, L. E. Nyquist, D. D. Bogard et al. 2001. Post-crystallization reheating and partial melting of eucrite EET90020 by impact into the hot crust of asteroid 4Vesta ~4.50Ga ago. Geochimica et Cosmochimica Acta 65, no. 20:3577–3599.
Zhou, Q., Q.-Z. Yin, B. Bottke, P. Claeys, X.-H. Li, F.-Y. Wu, Q.- L. Li, Y. Liu, and G.-Q. Tang. 2011. Early basaltic volcanism and late heavy bombardment on Vesta: U-Pb ages of small zircons and phosphates in eucrites. Lunar and Planetary Science Conference 42:#2575.
Zhou, Q., Q.-Z. Yin, E. D. Young, X.-H. Li, F.-Y. Wu, Q.-L. Li, Y. Liu, and G.-Q. Tang. 2013. SIMS Pb-Pb and U-Pb age determination of eucrite zircons at <5μm scale and the first 50Ma of the thermal history of Vesta. Geochimica et Cosmochimica Acta 110:152–175.
Zuber, M. T., H. Y. McSween Jr., R. P. Binzel, L. T. Elkins- Tanton, A.S. Konopliv, C.M. Pieters, and D. E. Smith. 2011. Origin, internal structure and evolution of 4 Vesta. Space Science Reviews 163:77–93.









