Information, Science and Biology
Originally published in Journal of Creation 10, no 2 (August 1996): 181-187.
Abstract
Energy and matter are considered to be basic universal quantities.
Summary
However, the concept of information has become just as fundamental and far-reaching, justifying its categorisation as the third fundamental quantity. One of the intrinsic characteristics of life is information. A rigorous analysis of the characteristics of information demonstrates that living things intrinsically reflect both the mind and will of their Creator.
Information confronts us at every turn both in technological and in natural systems: in data processing, in communications engineering, in control engineering, in the natural languages, in biological communications systems, and in information processes in living cells. Thus, information has rightly become known as the third fundamental, universal quantity. Hand in hand with the rapid developments in computer technology, a new field of study—that of information science—has attained a significance that could hardly have been foreseen only two or three decades ago. In addition, information has become an interdisciplinary concept of undisputed central importance to fields such as technology, biology and linguistics. The concept of information therefore requires a thorough discussion, particularly with regard to its definition, with understanding of its basic characteristic features and the establishment of empirical principles. This paper is intended to make a contribution to such a discussion.
Information: a statistical study
With his (1948) paper entitled ‘A Mathematical Theory of Communication’, Claude E. Shannon was the first to devise a mathematical definition of the concept of information. His measure of information which is given in bits (binary digits), possessed the advantage of allowing quantitative statements to be made about relationships that had previously defied precise mathematical description. This method has an evident drawback, however: information according to Shannon does not relate to the qualitative nature of the data, but confines itself to one particular aspect that is of special significance for its technological transmission and storage. Shannon completely ignores whether a text is meaningful, comprehensible, correct, incorrect or meaningless. Equally excluded are the important questions as to where the information comes from (transmitter) and for whom it is intended (receiver). As far as Shannon’s concept of information is concerned, it is entirely irrelevant whether a series of letters represents an exceptionally significant and meaningful text or whether it has come about by throwing dice. Yes, paradoxical though it may sound, considered from the point of view of information theory, a random sequence of letters possesses the maximum information content, whereas a text of equal length, although linguistically meaningful, is assigned a lower value.
The definition of information according to Shannon is limited to just one aspect of information, namely its property of expressing something new: information content is defined in terms of newness. This does not mean a new idea, a new thought or a new item of information—that would involve a semantic aspect—but relates merely to the greater surprise effect that is caused by a less common symbol. Information thus becomes a measure of the improbability of an event. A very improbable symbol is therefore assigned correspondingly high information content.
Before a source of symbols (not a source of information!) generates a symbol, uncertainty exists as to which particular symbol will emerge from the available supply of symbols (for example, an alphabet). Only after the symbol has been generated is the uncertainty eliminated. According to Shannon, therefore, the following applies: information is the uncertainty that is eliminated by the appearance of the symbol in question. Since Shannon is interested only in the probability of occurrence of the symbols, he addresses himself merely to the statistical dimension of information. His concept of information is thus confined to a non-semantic aspect. According to Shannon, information content is defined such that three conditions must be fulfilled:
Summation condition: The information contents of mutually independent symbols (or chains or symbols) should be capable of addition. The summation condition views information as something quantitative.
Probability condition: The information content to be ascribed to a symbol (or to a chain of symbols) should rise as the level of surprise increases. The surprise effect of the less common ‘z’ (low probability) is greater than that of the more frequent ‘e’ (high probability). It follows from this that the information content of a symbol should increase as its probability decreases.
The bit as a unit of information: In the simplest case, when the supply of symbols consists of just two symbols, which, moreover, occur with equal frequency, the information content of one of these symbols should be assigned a unit of precisely 1 bit. The following empirical principle can be derived from this:
Theorem 1: The statistical information content of a chain of symbols is a quantitative concept. It is given in bits (binary digits).
According to Shannon’s definition, the information content of a single item of information (an item of information in this context merely means a symbol, character, syllable, or word) is a measure of the uncertainty existing prior to its reception. Since the probability of its occurrence may only assume values between 0 and 1, the numerical value of the information content is always positive. The information content of a plurality of items of information (for example, characters) results (according to the summation condition) from the summation of the values of the individual items of information. This yields an important characteristic of information according to Shannon:
Theorem 2: According to Shannon’s theory, a disturbed signal generally contains more information than an undisturbed signal, because, in comparison with the undisturbed transmission, it originates from a larger quantity of possible alternatives.
Shannon’s theory also states that information content increases directly with the number of symbols. How inappropriately such a relationship describes actual information content becomes apparent from the following situation: If someone uses many words to say virtually nothing, then, according to Shannon, in accordance with the large number of letters, this utterance is assigned a very high information content, whereas the utterance of another person, who is skilled in expressing succinctly that which is essential, is ascribed only a very low information content.
Furthermore, in its equation of information content, Shannon’s theory uses the factor of entropy to take account of the different frequency distributions of the letters. Entropy thus represents a generalised but specific feature of the language used. Given an equal number of symbols (for example, languages that use the Latin alphabet), one language will have a higher entropy value than another language if its frequency distribution is closer to a uniform distribution. Entropy assumes its maximum value in the extreme case of uniform distribution.
Symbols: a look at their average information content
If the individual symbols of a long sequence of symbols are not equally probable (for example, text), what is of interest is the average information content for each symbol in this sequence as well as the average value over the entire language. When this theory is applied to the various code systems, the average information content for one symbol results as follows:
In the German language: I = 4.113 bits/letter
In the English language: I = 4.046 bits/letter
In the dual system: I = 1 bit/digit
In the decimal system: I = 3.32 bits/digit
In the DNA molecule: I = 2 bits/nucleotide
The highest information density
The highest information density known to us is that of the DNA (deoxyribonucleic acid) molecules of living cells. This chemical storage medium is 2 nm in diameter and has a 3.4 NM helix pitch (see Figure 1). This results in a volume of 10.68 x 10-21 cm3 per spiral. Each spiral contains ten chemical letters (nucleotides), resulting in a volumetric information density of 0.94 x 1021 letters/cm3. In the genetic alphabet, the DNA molecules contain only the four nucleotide bases, that is, adenine, thymine, guanine and cytosine. The information content of such a letter is 2 bits/nucleotide. Thus, the statistical information density is 1.88 x 1021 bits/cm3.
Proteins are the basic substances that compose living organisms and include, inter alia, such important compounds as enzymes, antibodies, haemoglobins and hormones. These important substances are both organ- and species-specific. In the human body alone, there are at least 50,000 different proteins performing important functions. Their structures must be coded just as effectively as the chemical processes in the cells, in which synthesis must take place with the required dosage in accordance with an optimised technology. It is known that all the proteins occurring in living organisms are composed of a total of just 20 different chemical building blocks (amino acids). The precise sequence of these individual building blocks is of exceptional significance for life and must therefore be carefully defined. This is done with the aid of the genetic code. Shannon’s information theory makes it possible to determine the smallest number of letters that must be combined to form a word in order to allow unambiguous identification of all amino acids. With 20 amino acids, the average information content is 4.32 bits/amino acid. If words are made up of two letters (doublets), with 4 bits/word, these contain too little information. Quartets would have 8 bits/word and would be too complex. According to information theory, words of three letters (triplets) having 6 bits/word are sufficient and are therefore the most economical method of coding. Binary coding with two chemical letters is also, in principle, conceivable. This however, would require a quintet to represent each amino acid and would be 67 per cent less economical than the use of triplets.
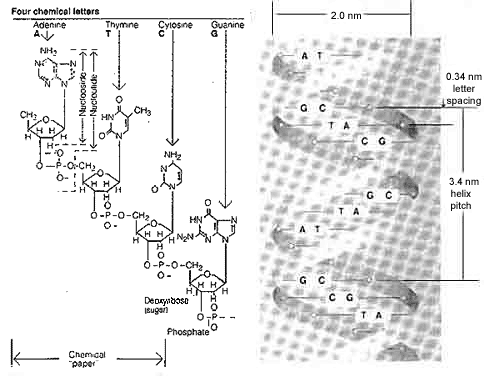
Figure 1. The DNA molecule—the universal storage medium of natural systems. A short section of a strand of the double helix with sugar-phosphate chain reveals its chemical structure (left). The schematic representation of the double helix (right) shows the base pairs coupled by hydrogen bridges (in a plane perpendicular to the helical axis).
Computer chips and natural storage media
Figures 1, 2 and 3 show three different storage technologies: the DNA molecule, the core memory, and the microchip. Let’s take a look at these.
Core memory: Earlier core memories were capable of storing 4,096 bits in an area of 6,400 mm2 (see Figure 2). This corresponds to an area storage density of 0.64 bits/mm2. With a core diameter of 1.24 mm (storage volume 7,936 mm3), a volumetric storage density of 0.52 bits/mm3 is obtained.

Figure 2. Detail of the TR440 computer’s core-memory matrix (Manufacturer: Computer Gesellschaft Konstanz).
1-Mbit DRAM: The innovative leap from the core memory to the semiconductor memory is expressed in striking figures in terms of storage density; present-day 1-Mbit DRAMs (see Figure 3) permit the storage of 1,048,576 bits in an area of approximately 50 mm2, corresponding to an area storage density of 21,000 bits/mm2. With a thickness of approximately 0.5 mm, we thus obtain a volumetric storage density of 42,000 bits/mm3. The megachip surpasses the core memory in terms of area storage density by a factor of 32,800 and in terms of volumetric storage density by a factor of 81,000.

Figure 3. The 1-Mbit DRAM—a dynamic random-access memory for 1,048,576 bits.
DNA molecule: The carriers of genetic information, which perform their biological functions throughout an entire life, are nucleic acids. All cellular organisms and many viruses employ DNAs that are twisted in an identical manner to form double helices; the remaining viruses employ single-stranded ribonucleic acids (RNA). The figures obtained from a comparison with man-made storage devices are nothing short of astronomical if one includes the DNA molecule (see Figure 1). In this super storage device, the storage density is exploited to the physico-chemical limit: its value for the DNA molecule is 45 x 1012 times that of the megachip. What is the explanation for this immense difference of 45 trillion between VLSI technology and natural systems? There are three decisive reasons:
- The DNA molecule uses genuine volumetric storage technology, whereas storage in computer devices is area-oriented. Even though the structures of the chips comprise several layers, their storage elements only have a two-dimensional orientation.
- Theoretically, one single molecule is sufficient to represent an information unit. This most economical of technologies has been implemented in the design of the DNA molecule. In spite of all research efforts on miniaturisation, industrial technology is still within the macroscopic range.
- Only two circuit states are possible in chips; this leads to exclusively binary codes. In the DNA molecule, there are four chemical symbols (see Figure 1); this permits a quaternary code in which one state already represents 2 bits.
The knowledge currently stored in the libraries of the world is estimated at 1018 bits. If it were possible for this information to be stored in DNA molecules, 1 per cent of the volume of a pinhead would be sufficient for this purpose. If, on the other hand, this information were to be stored with the aid of megachips, we would need a pile higher than the distance between the earth and the moon.
The five levels of information
Shannon’s concept of information is adequate to deal with the storage and transmission of data, but it fails when trying to understand the qualitative nature of information.
Theorem 3: Since Shannon’s definition of information relates exclusively to the statistical relationship of chains of symbols and completely ignores their semantic aspect, this concept of information is wholly unsuitable for the evaluation of chains of symbols conveying a meaning.
In order to be able adequately to evaluate information and its processing in different systems, both animate and inanimate, we need to widen the concept of information considerably beyond the bounds of Shannon’s theory. Figure 4 illustrates how information can be represented as well as the five levels that are necessary for understanding its qualitative nature.
Level 1: statistics
Shannon’s information theory is well suited to an understanding of the statistical aspect of information. This theory makes it possible to give a quantitative description of those characteristics of languages that are based intrinsically on frequencies. However, whether a chain of symbols has a meaning is not taken into consideration. Also, the question of grammatical correctness is completely excluded at this level.
Level 2: syntax
In chains of symbols conveying information, the stringing-together of symbols to form words as well as the joining of words to form sentences are subject to specific rules, which, for each language, are based on consciously established conventions. At the syntactical level, we require a supply of symbols (code system) in order to represent the information. Most written languages employ letters; however, an extremely wide range of conventions is in use for various purposes: Morse code, hieroglyphics, semaphore, musical notes, computer codes, genetic codes, figures in the dance of foraging bees, odour symbols in the pheromone languages of insects, and hand movements in sign language.
The field of syntax involves the following questions:
- Which symbol combinations are defined characters of the language (code)?
- Which symbol combinations are defined words of the particular language (lexicon, spelling)?
- How should the words be positioned with respect to one another (sentence formation, word order, style)? How should they be joined together? And how can they be altered within the structure of a sentence (grammar)?
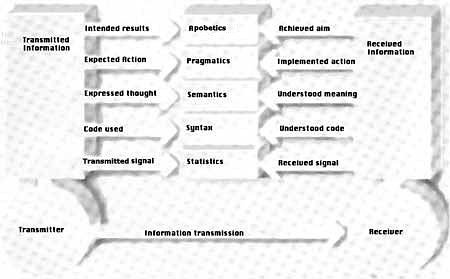
Figure 4. The five mandatory levels of information (middle) begin with statistics (at the lowest level). At the highest level is apobetics (purpose).
The syntax of a language, therefore, comprises all the rules by which individual elements of language can or must be combined. The syntax of natural languages is of a much more complex structure than that of formalised or artificial languages. Syntactical rules in formalised languages must be complete and unambiguous, since, for example, a compiler has no way of referring back to the programmer’s semantic considerations. At the syntactical level of information, we can formulate several theorems to express empirical principles:
Theorem 4: A code is an absolutely necessary condition for the representation of information.
Theorem 5: The assignment of the symbol set is based on convention and constitutes a mental process.
Theorem 6: Once the code has been freely defined by convention, this definition must be strictly observed thereafter.
Theorem 7: The code used must be known both to the transmitter and receiver if the information is to be understood.
Theorem 8: Only those structures that are based on a code can represent information (because of Theorem 4). This is a necessary, but still inadequate, condition for the existence of information.
These theorems already allow fundamental statements to be made at the level of the code. If, for example, a basic code is found in any system, it can be concluded that the system originates from a mental concept.
Level 3: semantics
Chains of symbols and syntactical rules form the necessary precondition for the representation of information. The decisive aspect of a transmitted item of information, however, is not the selected code, the size, number or form of the letters, or the method of transmission (script, optical, acoustic, electrical, tactile or olfactory signals), but the message it contains, what it says and what it means (semantics). This central aspect of information plays no part in its storage and transmission. The price of a telegram depends not on the importance of its contents but merely on the number of words. What is of prime interest to both sender and recipient, however, is the meaning; indeed, it is the meaning that turns a chain of symbols into an item of information. It is in the nature of every item of information that it is emitted by someone and directed at someone. Wherever information occurs, there is always a transmitter and a receiver. Since no information can exist without semantics, we can state:
Theorem 9: Only that which contains semantics is information.
According to a much-quoted statement by Norbert Wiener, the founder of cybernetics and information theory, information cannot be of a physical nature:
‘Information is information, neither matter nor energy. No materialism that fails to take account of this can survive the present day.’
The Dortmund information scientist Werner Strombach emphasises the non-material nature of information when he defines it as ‘an appearance of order at the level of reflective consciousness.’ Semantic information, therefore, defies a mechanistic approach. Accordingly, a computer is only ‘a syntactical device’ (Zemanek) which knows no semantic categories. Consequently, we must distinguish between data and knowledge, between algorithmically conditioned branches in a programme and deliberate decisions, between comparative extraction and association, between determination of values and understanding of meanings, between formal processes in a decision tree and individual selection, between consequences of operations in a computer and creative thought processes, between accumulation of data and learning processes. A computer can do the former; this is where its strengths, its application areas, but also its limits lie. Meanings always represent mental concepts; we can therefore further state:
Theorem 10: Each item of information needs, if it is traced back to the beginning of the transmission chain, a mental source (transmitter).
Theorems 9 and 10 basically link information to a transmitter (intelligent information source). Whether the information is understood by a receiver or not does nothing to change its existence. Even before they were deciphered the inscriptions in Egyptian obelisks were clearly regarded as information, since they obviously did not originate from a random process. Before the discovery of the Rosetta Stone (1799), the semantics of these hieroglyphics was beyond the comprehension of any contemporary person (receiver); nevertheless, these symbols still represented information.
All suitable formant devices (linguistic configurations) that are capable of expressing meanings (mental substrates, thoughts, contents of consciousness) are termed languages. It is only by means of language that information may be transmitted and stored on physical carriers. The information itself is entirely invariant, both with regard to change of transmission system (acoustic, optical, electrical) and also of storage system (brain, book, computer system, magnetic tape). The reason for this invariance lies in its non-material nature. We distinguish between different kinds of languages:
- Natural languages: at present, there are approximately 5,100 living languages on earth.
- Artificial or sign languages: Esperanto, sign language, semaphore, traffic signs.
- Artificial (formal) languages: logical and mathematical calculations, chemical symbols, shorthand, algorithmic languages, programming languages.
- Specialist languages in engineering: building plans, design plans, block diagrams, bonding diagrams, circuit diagrams in electrical engineering, hydraulics, pneumatics.
- Special languages in the living world: genetic language, the foraging-bee dance, pheromone languages, hormone language, signal system in a spider’s web, dolphin language, instincts (for example, flight of birds, migration of salmon).
Common to all languages is that these formant devices use defined systems of symbols whose individual elements operate with fixed, uniquely agreed rules and semantic correspondences. Every language has units (for example, morphemes, lexemes, phrases and whole sentences in natural languages) that act as semantic elements (formatives). Meanings are correspondences between the formatives, within a language, and imply a unique semantic assignment between transmitter and receiver.
Any communication process between transmitter and receiver consists of the formulation and comprehension of the sememes (sema = sign) in one and the same language. In the formulation process, the thoughts of the transmitter generate the transmissible information by means of a formant device (language). In the comprehension process, the combination of symbols is analysed and imaged as corresponding thoughts in the receiver.
Level 4: pragmatics
Up to the level of semantics, the question of the objective pursued by the transmitter in sending information is not relevant. Every transfer of information is, however, performed with the intention of producing a particular result in the receiver. To achieve the intended result, the transmitter considers how the receiver can be made to satisfy his planned objective. This intentional aspect is expressed by the term pragmatics. In language, sentences are not simply strung together; rather, they represent a formulation of requests, complaints, questions, inquiries, instructions, exhortations, threats and commands, which are intended to trigger a specific action in the receiver. Strombach defines information as a structure that produces a change in a receiving system. By this, he stresses the important aspect of action. In order to cover the wide variety of types of action, we may differentiate between:
- Modes of action without any degree of freedom (rigid, indispensable, unambiguous, program-controlled), such as program runs in computers, machine translation of natural languages, mechanised manufacturing operations, the development of biological cells, the functions of organs;
- Modes of action with a limited degree of freedom, such as the translation of natural languages by humans and instinctive actions (patterns of behaviour in the animal kingdom);
- Modes of action with the maximum degree of freedom (flexible, creative, original; only in humans), for example, acquired behaviour (social deportment, activities involving manual skills), reasoned actions, intuitive actions and intelligent actions based on free will.
All these modes of action on the part of the receiver are invariably based on information that has been previously designed by the transmitter for the intended purpose.
Level 5: apobetics
The final and highest level of information is purpose. The concept of apobetics has been introduced for this reason by linguistic analogy with the previous definitions. The result at the receiving end is based at the transmitting end on the purpose, the objective, the plan, or the design. The apobetic aspect of information is the most important one, because it inquires into the objective pursued by the transmitter. The following question can be asked with regard to all items of information: Why is the transmitter transmitting this information at all? What result does he/she/it wish to achieve in the receiver? The following examples are intended to deal somewhat more fully with this aspect:
- Computer programmes are target-oriented in their design (for example, the solving of a system of equations, the inversion of matrices, system tools).
- With its song, the male bird would like to gain the attention of the female or to lay claim to a particular territory.
- With the advertising slogan for a detergent, the manufacturer would like to persuade the receiver to decide in favour of its product.
- Humans are endowed with the gift of natural language; they can thus enter into communication and can formulate objectives.
We can now formulate some further theorems:
Theorem 11: The apobetic aspect of information is the most important, because it embraces the objective of the transmitter. The entire effort involved in the four lower levels is necessary only as a means to an end in order to achieve this objective.
Theorem 12: The five aspects of information apply both at the transmitter and receiver ends. They always involve an interaction between transmitter and receiver (see Figure 4).
Theorem 13: The individual aspects of information are linked to one another in such a manner that the lower levels are always a prerequisite for the realisation of higher levels.
Theorem 14: The apobetic aspect may sometimes largely coincide with the pragmatic aspect. It is, however, possible in principle to separate the two.
Having completed these considerations, we are in a position to formulate conditions that allow us to distinguish between information and non-information. Two necessary conditions (NCs; to be satisfied simultaneously) must be met if information is to exist:
NC1: A code system must exist.
NC2: The chain of symbols must contain semantics.
Sufficient conditions (SCs) for the existence of information are:
SC1: It must be possible to discern the ulterior intention at the semantic, pragmatic and apobetic levels (example: Karl v. Frisch analysed the dance of foraging bees and, in conformance with our model, ascertained the levels of semantics, pragmatics and apobetics. In this case, information is unambiguously present).
SC2: A sequence of symbols does not represent information if it is based on randomness. According to G.J. Chaitin, an American informatics expert, randomness cannot, in principle, be proven; in this case, therefore, communication about the originating cause is necessary.
The above information theorems not only play a role in technological applications, they also embrace all otherwise occurring information (for example, computer technology, linguistics, living organisms).
Information in living organisms
Life confronts us in an exceptional variety of forms; for all its simplicity, even a monocellular organism is more complex and purposeful in its design than any product of human invention. Although matter and energy are necessary fundamental properties of life, they do not in themselves imply any basic differentiation between animate and inanimate systems. One of the prime characteristics of all living organisms, however, is the information they contain for all operational processes (performance of all life functions, genetic information for reproduction). Braitenberg, a German cybernetist, has submitted evidence ‘that information is an intrinsic part of the essential nature of life.’ The transmission of information plays a fundamental role in everything that lives. When insects transmit pollen from flower blossoms, (genetic) information is essentially transmitted; the matter involved in this process is insignificant. Although this in no way provides a complete description of life as yet, it touches upon an extremely crucial factor.
Without a doubt, the most complex information processing system in existence is the human body. If we take all human information processes together, that is, conscious ones (language, information-controlled functions of the organs, hormone system), this involves the processing of 1024 bits daily. This astronomically high figure is higher by a factor of 1,000,000 than the total human knowledge of 1018 bits stored in all the world’s libraries.
The concept of information
On the basis of Shannon’s information theory, which can now be regarded as being mathematically complete, we have extended the concept of information as far as the fifth level. The most important empirical principles relating to the concept of information have been defined in the form of theorems. Here is a brief summary of them:1
- No information can exist without a code.
- No code can exist without a free and deliberate convention.
- No information can exist without the five hierarchical levels: statistics, syntax, semantics, pragmatics and apobetics.
- No information can exist in purely statistical processes.
- No information can exist without a transmitter.
- No information chain can exist without a mental origin.
- No information can exist without an initial mental source; that is, information is, by its nature, a mental and not a material quantity.
- No information can exist without a will.
The Bible has long made it clear that the creation of the original groups of fully operational living creatures, programmed to transmit their information to their descendants, was the deliberate act of the mind and the will of the Creator, the great Logos Jesus Christ.
We have already shown that life is overwhelmingly loaded with information; it should be clear that a rigorous application of the science of information is devastating to materialistic philosophy in the guise of evolution, and strongly supportive of Genesis creation.2
Footnotes
- This paper has presented only a qualitative survey of the higher levels of information. A quantitative survey is among the many tasks still to be performed.
- This paper has been adapted from a paper entitled ‘Information: the third fundamental quantity’ that was published in the November/December 1989 issue of Siemens Review (Vol. 56, No. 6).
Recommended Resources

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- Available Monday–Friday | 9 AM–5 PM ET
- © 2025 Answers in Genesis


