Do Creationists Believe in “Weird” Physics like Relativity, Quantum Mechanics, and String Theory?

Science is the study of the natural world using the five senses. Because people use their senses every day, people have always done some sort of science. However, good science requires a systematic approach. While ancient Greek science did rely upon some empirical evidence, it was heavily dominated by deductive reasoning. Science as we know it began in the 17th century. The father of the scientific method is Sir Francis Bacon (1561–1626), who clearly defined the scientific method in his Novum Organum (1620). Bacon also introduced inductive reasoning, which is the foundation of the scientific method.

The first step in the scientific method is to define clearly a problem or question about how some aspect of the natural world operates. Some preliminary investigation of the problem can lead one to form a hypothesis. A hypothesis is an educated guess about an underlying principle that will explain the phenomenon that we are trying to explain. A good hypothesis can be tested. That is, a hypothesis ought to make predictions about certain observable phenomena, and we can devise an experiment or observation to test those predictions. If we conduct the experiment or observation and find that the predictions match the results, then we say that we have confirmed our hypothesis, and we have some confidence that our hypothesis is correct. On the other hand, if our predictions are not borne out, then we say that our hypothesis is disproved, and we can either alter our hypothesis or develop a new one and repeat the process of testing. After repeated testing with positive results, we say that the hypothesis is confirmed, and we have confidence that our hypothesis is correct.

Properly applied inductive reasoning does not necessarily lead to a true conclusion.

Notice that we did not “prove” the hypothesis, but that we merely confirmed it. This is a big difference between deductive and inductive reasoning. If we have a true premise, then properly applied deductive reasoning will lead to a true conclusion. However, properly applied inductive reasoning does not necessarily lead to a true conclusion. How can this be? Our hypothesis may be one of several different hypotheses that produce the same experimental or observational results. It is very easy to assume that our hypothesis, when confirmed, is the end of the matter. However, our hypothesis may make other predictions that future, different tests may not confirm. If this happens, then we must further modify or abandon our hypothesis to explain the new data. The history of science is filled with examples of this process, and we ought to expect that this will continue.

This puts the scientist in a peculiar position. While we can definitely disprove a number of propositions, we can never be entirely sure that what we believe to be true is indeed true. Thus, science is a very changing thing. History shows that scientific “truth” changes over time. The uncertainty is the reason why continued testing of our ideas is so important in science. Once we test a hypothesis many times, we gain enough confidence that it is correct, and we eventually begin to call our hypothesis a theory. So a theory is a grown-up, well-developed hypothesis.

At one time, scientists conferred the title of law to well-established theories. This use of the word “law” probably stemmed from the idea that God had imposed some order (law) onto the universe, and our description of how the world operates is a statement of this fact. However, with a less Christian understanding of the world, scientists have departed from using the word law. Scientists continue to refer to older ideas, such as Newton’s law of gravity or laws of motion as law, but no one has termed any new ideas in science as law for a very long time.

Isaac Newton (1643–1727)

In 1687, Sir Isaac Newton (1643–1727) published his Principia, which detailed work that he had done about two decades earlier. In the Principia, Newton presented his law of gravity and laws of motion, which are the foundation of the branch of physics known as mechanics. Because he required a mathematical framework to present his ideas, Newton invented calculus. His great breakthrough was to hypothesize that the force that held us to the earth was the same force that kept the moon orbiting around the earth each month. From knowledge of the moon’s distance from the earth and orbital period, Newton used his laws of motion to conclude that the moon is accelerated toward the earth 1/3600 of the measured acceleration of gravity at the surface of the earth. The fact that we on the earth’s surface are 60 times closer to the earth’s center than the moon allowed Newton to devise his inverse square law for gravity (60² = 3,600).

This unity of gravity on the earth and the force between the earth and moon was a good hypothesis, but could Newton test it? Yes. When Newton applied his laws of gravity and motion to the then-known planets orbiting the sun (Mercury, Venus, Earth, Mars, Jupiter, and Saturn), he was able to predict several things:

1. The planets orbit the sun in elliptical orbits with the sun at one focus of the ellipses.
2. The line between the sun and a planet sweeps out equal areas in equal intervals of time.
3. The square of a planet’s orbital period is proportional to the third power of the planet’s mean distance from the sun.

Johannes Kepler (1571–1630)

These three statements are known as Kepler’s three laws of planetary motion, because the German mathematician Johannes Kepler (1571–1630) had found them in a slightly different form several decades before Newton. Kepler empirically found his three laws by studying data on planetary motions taken by the Danish astronomer Tycho Brahe (1546–1601) over a period of 20 years in the latter part of the 16th century. Kepler arrived at his result by laborious trial and error for over two decades, but he had no explanation of why the planets behaved the way that they did. Newton easily showed (or predicted) that the planets must follow Kepler’s law as a consequence of his law of gravity.

Many other predictions of Newton’s new physics followed. Besides Earth, Jupiter and Saturn had satellites that obeyed Newton’s formulation of Kepler’s three laws. Newton’s good friend who privately funded the publication of the Principia, Sir Edmond Halley (1656–1742), applied Newton’s work to the observed motions of comets. He found that comets also followed the laws, but that their orbits were much more elliptical and inclined than the orbits of planets. In his study, Halley noticed that one comet that he observed had an orbit identical to one seen about 75 years before and that both comets had a 75-year orbital period. Of course, when the comet returned once again, Halley was long dead, but this comet bears his name.

In 1704, Newton first published his other seminal work in physics, Optics. In this book, he presented his theory of the wave nature of light. Together, his Principia and Optics laid the foundation of physics as we know it. Over the next two centuries, scientists applied Newtonian physics to all sorts of situations, and in each case the predictions of the theory were borne out by experiment and observation. For instance, William Herschel stumbled upon the planet Uranus in 1781, and its orbit followed Kepler’s three laws as well. However, by 1840, astronomers found that there were slight discrepancies between the predicted and observed motion of Uranus. Two mathematicians independently hypothesized that there was an additional planet beyond Uranus whose gravity was tugging on Uranus. This led to the discovery of Neptune in 1846. These successes gave scientists a tremendous confidence in Newtonian physics, and thus Newtonian physics is one of the most well-established theories in history. However, by the end of the 19th century, experimental results began to conflict with Newtonian physics.

Quantum Mechanics

Near the end of the 19th century, physicists turned their attention to how hot objects radiate, with one practical application being the improvement of efficiency of the filament of the recently invented light bulb. Noting that at low temperatures good absorbers and emitters of radiation appear black, they dubbed a perfect absorber and emitter of radiation a black body. Physicists experimentally determined that a black body of a certain temperature emitted the greatest amount of energy at a certain frequency and that the amount of energy that it radiated diminished toward zero at higher and lower frequencies. Attempts to explain this behavior with classical, or Newtonian, physics worked very well at most frequencies but failed miserably at higher frequencies. In fact, at very high frequencies, classical physics required that the energy emitted increase toward infinity.

Max Planck (1858–1947)

In 1901, the German physicist Max Planck (1858–1947) proposed a solution. He suggested that the energy radiated from a black body was not exactly in waves as Newton had shown, but was instead carried away by tiny particles (later called photons). The energy of each photon was proportional to its frequency. This was a radical departure from classical physics, but this new theory did exactly explain the spectra of black bodies.

In 1905, the German-born physicist Albert Einstein (1879–1955) used Planck’s theory to explain the photoelectric effect. What is the photoelectric effect? A few years earlier, physicists had discovered that when light shone on a metal to which an electric potential was applied, electrons were emitted. Attempts to explain the details of this phenomenon with classical physics had failed, but Einstein’s application of Planck’s theory explained it very well.

Other problems with classical physics had mounted. Physicists found that excited gas in a discharge tube emitted energy at certain discrete wavelengths or frequencies. The exact wavelengths of emission depended upon the composition of the gas, with hydrogen gas having the simplest spectrum. Several physicists investigated the problem, with the Swedish scientist Johannes Rydberg (1854–1919) offering the most general description of the hydrogen spectrum in 1888. However, Ryberg did not offer a physical explanation. Indeed, there was no classical physics explanation for the spectral behavior of hydrogen gas until 1913, when the Danish physicist Niels Bohr (1885–1962) published his model of the hydrogen atom that did explain hydrogen’s spectrum.

In the Bohr model, the electron orbits the proton only at certain discrete distances from the proton, whereas in classical physics the electron can orbit at any distance from the proton. In classical physics the electron must continually emit radiation as it orbits, but in Bohr’s model the electron emits energy only when it leaps from one possible orbit to another. Bohr’s explanation of the hydrogen atom worked so well that scientists assumed that it must work for other atoms as well. The hydrogen atom is very simple, because it consists of only two particles, a proton and an electron. Other atoms have increasing numbers of particles (more electrons orbiting the nucleus, which contains more protons as well as neutrons) which makes their solutions much more difficult, but the Bohr model worked for them as well. The Bohr model is essentially the model that most of us learned in school.

While Bohr’s model was obviously successful, it seemed to pull some new principles out of the air, and those principles contradicted principles of classical physics. Physicists began to search for a set of underlying unifying principles to explain the model and other aspects of the emerging new physics. We will omit the details, but by the mid-1920s, those new principles were in place. The basis of this new physics is that in very small systems, as within atoms, energy can exist in only certain small, discrete amounts with gaps between adjacent values. This is radically different from classical physics, where energy can assume any value. We say that energy is quantized because it can have only certain discrete values, or quanta. The mathematical theory that explains the energies of small systems is called quantum mechanics.

Quantum mechanics is a very successful theory. Since its introduction in the 1920s, physicists have used it to correctly predict the behavior and characteristics of elementary particles, nuclei of atoms, atoms, and molecules. Many facets of modern electronics are best understood in terms of quantum mechanics. Physicists have developed many details and applications of the theory, and they have built other theories upon it.

Quantum mechanics is a very successful theory, yet a few people do not accept it. Why? There are several reasons. One reason for rejection is that the postulates of quantum mechanics just do not feel right. They violate our everyday understanding of how the physical world works. However, the problem is that very small particles, such as electrons, do not behave the same way that everyday objects do. We invented quantum mechanics to explain small things such as electrons because our everyday understanding of the world fails to explain them. The peculiarities of quantum mechanics disappear as we apply quantum mechanics to larger systems. As we increase the size and scope of small systems, we find that the oddities of quantum mechanics tend to smear out and assume properties more like our common-sense perceptions. That is, the peculiarities of quantum mechanics disappear in larger, macroscopic systems.

Another problem that people have with quantum mechanics is certain interpretations applied to quantum mechanics. For instance, one of the important postulates of quantum mechanics is the Schrödinger wave equation. When we apply the Schrödinger equation to a particle such as an electron, we get a mathematical wave as a description of the particle. What does this wave mean? Early on, physicists realized that the wave represented a probability distribution. Where the wave had a large value, the probability was large of finding the particle in that location, but where the wave had low value, there was little probability of finding the particle there. This is strange. Newtonian physics had led to determinism—the absolute knowledge of where a particle was at a particular time from the forces and other information involved. Yet, the probability function does accurately predict the behavior of small particles such as electrons. Even Albert Einstein, whose early work led to much of quantum mechanics, never liked this probability. He once famously remarked, “God does not play dice with the universe.” Erwin Schrödinger (1887–1961), who had formulated his famous Schrödinger equation stated in 1926, “If we are going to stick to this ****** quantum-jumping, then I regret that I ever had anything to do with quantum theory.”

Note that with the probability distribution we cannot know precisely where a particle is located. A statement of this is the Heisenberg Uncertainty Principle (named for Werner Heisenberg, 1901–1976). We explain this by acknowledging that particles such as electrons have a wave nature as well as a particle nature. For that matter, we also believe that waves (such as light and sound) also have a particle nature. This wave-particle duality is a bit strange to us, because we do not sense it in everyday experience, but it is borne out by numerous experimental results.

For instance, let us consider a double slit experiment. If we send a wave toward an obstruction with two slits in it, the wave will pass through both slits and produce a distinctive interference pattern behind the slits. This is because the wave passes through both slits. If we send a large number of electrons toward a similar apparatus, the electrons will also produce an interference pattern behind the slits, suggesting that the electrons (or their wave functions) went through both slits. However, if we send one electron at a time toward the slits and look for the emergence of each electron behind the slits, we will find that each electron will emerge through one slit or the other, but not both. How can this be? Indeed, this is perplexing. The most common resolution is the Copenhagen interpretation, named for the city where it was developed. This interpretation posits that an individual electron does not go through either slit, but instead exists in some sort of meta-stable state between the two states until we observe (detect) the electrons. At the point of observation, the electron’s wave equation collapses, allowing the electron to assume one state or the other. Now, this is weird, but most alternate explanations are even weirder, so you might understand why some people may have a problem with quantum mechanics.

Classical physics introduced determinism, quantum mechanics introduced indeterminism.

Is there a way out of this dilemma? Yes. Why do we need an interpretation to quantum mechanics? No one demanded any such interpretation of Newtonian physics. No one asked, “What does it mean?” There is no meaning, other than the fact that Newtonian physics does a good job of describing what we see in the macroscopic world. The same ought to be true for quantum mechanics. It does a good job of describing the microscopic world. Whereas classical physics introduced determinism, quantum mechanics introduced indeterminism. This indeterminism is fundamental in the sense that uncertainty in outcome will still exist even if we have all knowledge of the relevant input parameters. Newtonian determinism fit well with the concept of God’s sovereignty, but the fundamental uncertainty of quantum mechanics appears to rob God of that attribute. However, this assumes that quantum mechanics is a complete theory, that is, that quantum mechanics is an ultimate theory. There are limits to the applications of quantum mechanics, such as the fact that there is no theory of quantum gravity. If the history of science is any teacher, we can expect that quantum mechanics will one day be replaced by some other theory. This other theory probably will include quantum mechanics as a special case of the better theory. That theory may clear up the uncertainty question.

As an aside, we perhaps ought to mention that the determinism derived from Newtonian physics also produces a conclusion unpalatable to many Christians. If determinism is true, then all future events are predetermined from the initial conditions of the universe. Just as the Copenhagen interpretation of quantum mechanics led to even God not being able to know the outcome of an experiment, many people applying determinism concluded that God was unable to alter the outcome of an experiment. That is, God was bound by the physics that rules the universe. This quickly led to deism. Most, if not all, people today who reject quantum mechanics refuse to accept this extreme interpretation of Newtonian physics. They ought to recognize that just as determinism is a perversion of Newtonian physics, the Copenhagen interpretation is a perversion of quantum mechanics.

The important point is that just as classical mechanics does a good job in describing the macroscopic world, quantum mechanics does a good job in describing the microscopic world. We ought not expect any more of a theory. Consequently, most physicists who believe the biblical account of creation have no problem with quantum mechanics.

Relativity

There are two theories of relativity, the special and general theories. We will briefly describe the special theory of relativity first. Even before Newton, Galileo (1564–1642) had conducted experiments with moving bodies. He realized that if we move toward or away from a moving object, the relative speed that we measure for that object depends upon that object’s motion and our motion. This Galilean relativity is a part of Newtonian mechanics. The same behavior is true for the speed of waves. For instance, if we ride in a boat moving through water with waves, the speed of the waves that we measure will depend upon our motion and on the motion of the waves. In 1881, Albert A. Michelson (1852–1931) conducted a famous experiment that he refined and repeated in 1887 with Edward W. Morley (1838–1923). In this experiment, they measured the speed of light parallel and perpendicular to our annual motion around the sun. Much to their surprise, they found that the speed of light was the same regardless of the direction they measured it. This null result baffled physicists, for if taken at face value, it suggested that the earth did not orbit the sun, while there is other evidence that the earth does indeed orbit the sun.

In 1905, Albert Einstein took the invariance of the speed of light as a postulate and worked out its consequences. He made three predictions concerning an object as its speed approaches the speed of light:

1. The length of the object as it passes will appear to shorten toward zero.
2. The object’s mass will increase without bound.
3. The passage of time as measured by the object will approach zero.

These behaviors are strange and do not conform to what we might expect from everyday experience, but keep in mind that in everyday experience we do not encounter objects moving at any speed close to that of light.

Eventually, these predictions were confirmed in experiments. For instance, particle accelerators accelerate small particles to very high speeds. We can measure the masses of the particles as we accelerate them, and their masses increase in the manner predicted by the theory. In other experiments, very fast-moving, short-lived particles exist longer than they do when moving very slowly. The rate of time dilation is consistent with the predictions of the theory. Length contraction is a little more difficult to directly test, but we have tested it as well.

Relativity Confirmed

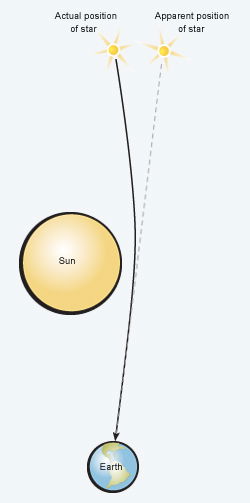
In 1919 a total eclipse of the sun allowed scientists to confirm Einstein’s general theory of relativity. As a result of the sun’s gravitation, stars appeared to be displaced from their true positions, just as Einstein’s theory predicted.

Einstein’s theory of special relativity applies to particles moving at a constant rate but does not address their acceleration. Einstein addressed that problem with his general theory in 1916, but he also treated the acceleration due to gravity. In general relativity, space and time are physical things that have a structure in some ways similar to a fabric. Einstein treated time as a fourth dimension in addition to the normal three dimensions of space. We sometimes call this four-dimensional entity space-time or simply space. The presence of a large amount of matter or energy (Einstein previously had shown their equivalence) alters space. Mathematically, the alteration of space is like a curvature, so we say that matter or energy bends space. The curvature of space telegraphs the presence of matter and energy to other matter and energy in space, and this more deeply answered a question about gravity. Newton had hypothesized that gravity operated through empty space, but his theory could not explain at all how the information about an object’s mass and distance was transmitted through space. In general relativity, an object must move through a straight line in space-time, but the curvature of space-time induced by nearby mass causes that straight-line motion to appear to us as acceleration.

Einstein’s new theory made several predictions. The first opportunity to test the theory happened during a total solar eclipse in 1919. During the eclipse, astronomers were able to photograph stars around the edge of the sun. The light from those stars had to pass very close to the sun to get to the earth. As the stars’ light passed near the sun, the sun attracted the light via the curvature of space-time. This caused the stars to appear farther from the sun than they would have otherwise. Newtonian gravity also predicts a deflection of starlight toward the sun, but the deflection is less than with general relativity. The observed amount of deflection was consistent with the predictions of general relativity. Astronomers have repeated the experiment many times since 1919 with ever-improving accuracy.

For many years, radio astronomers have measured with great precision the locations of distant-point radio sources as the sun passed by, and those results beautifully agree with the predictions. Another early confirmation was the explanation of a small anomaly in the orbit of the planet Mercury that Newtonian gravity could not explain. Many other experiments of various types have repeatedly confirmed general relativity. Some experiments today even allow us to test for slight variations of Einstein’s theory.

We can apply general relativity to the universe as a whole. Indeed, when we do this, we discover that it predicts that the universe is either expanding or contracting; it is a matter of observation to determine which the universe actually is doing. In 1928, Edwin Hubble (1889–1953) showed that the universe is expanding. Most people today think that the expansion began with the big bang, the supposed sudden appearance of the universe 13.7 billion years ago. However, there are many other possibilities. For instance, the creation physicist Russell Humphreys proposed his white hole cosmology, assuming that general relativity is the correct theory of gravity (see his book Starlight and Time1). It is interesting to note that universal expansion is consistent with certain Old Testament passages (e.g., Psalm 104:2) that mention the stretching of the heavens.

Seeing that there is so much evidence to support Einstein’s theory of general relativity, why do some creationists oppose the theory? There are at least three reasons. One reason is that, as with quantum mechanics, modern relativity theory appears to violate certain common-sense views of the way that the world works. For instance, in everyday experience, we don’t see mass change and time appear to slow. Indeed, general relativity forces us to abandon the concept of simultaneity of time. Simultaneity means that time progresses at the same rate for all observers, regardless of where they are. As we previously stated, in special relativity, time slows with greater speed. However, with general relativity, the rate at which time passes depends not only upon speed but also on one’s location in a gravitational field. The deeper one is in a gravitational field, the slower that time passes. For example, a clock at sea level will record the passage of time more slowly than a clock at mile-high Denver. Admittedly, this is weird. However, the discrepancy between the clocks at these two locations is so miniscule as to not appear on most clocks, save the most accurate atomic clocks. This sort of thing has been measured several times, and the discrepancies between the clocks involved always are the same as those predicted by theory. Thus, while our perception is that time flows uniformly everywhere, the reality is that the passage of time does depend upon one’s location, but the differences are so small in the situations encountered on the earth that we cannot perceive them. That is, the predictions of general relativity on earth are consistent with our ability to perceive time. However, there are conditions beyond the earth that the loss of simultaneity would be very obvious if we could experience them.

A second reason why some creationists oppose modern relativity theory is the misappropriation of modern relativity theory to support moral relativism. Unfortunately, modern relativity theory arose at precisely the time that moral relativism became popular. Moral relativists proclaim that “all things are equal,” and they were very eager to snatch some of the triumph of relativity theory to support their cause. There are at least two problems with this misappropriation. First, it does not follow that a principle that works in the natural world automatically operates in the world of morality. The physical world is material, but the world of morality is immaterial. Second, the moral relativists either did not understand relativity or they intentionally misused it. Despite the common misconception, modern relativity theory does not tell us that everything is relative. There are absolutes in modern theory of relativity. The speed of light is a constant. While the passage of time may vary, general relativity provides an absolute way in which to compare the passage of time in two reference frames. The modern theory of relativity in no way supports moral relativism.

The third reason why some creationists reject modern relativity theory is that they think that general relativity inevitably leads to the big-bang model. However, the big-bang model is just one possible origin scenario for the universe; there are many other possibilities. We have already mentioned Russ Humphreys’s white hole cosmology, and there are other possible recent creation models based upon general relativity. True—if general relativity is not correct, then the big-bang model would be in trouble. However, if general relativity is correct, then the shortcut attempt to undermine the big-bang model will doom us from ever finding the correct cosmology.

String Theory

With the establishment of quantum mechanics in the 1920s, the development of the science of particle physics soon followed. At first, only a few particles were known: the electron, proton, and neutron. These particles all had mass and were thought at the time to be the fundamental building blocks of matter. Quantum mechanics introduced the concept that material particles could be described by waves, and conversely that waves could be described by particles. That led to the concept of particles that had no mass, such as photons, the particles that make up light. Eventually, physicists saw the need for other particles, such as neutrinos and antiparticles. Evidence for these odd particles soon followed. Experimental results suggested the existence of other particles, such as the meson, muon, and tau particles, as well as their antiparticles. Many of these new particles were very short-lived, but they were particles nevertheless.

Physicists began to see patterns in the growing zoo of particles. They could group particles according to certain properties. For instance, elementary particles possess angular momentum, a property normally associated with spinning objects, so physicists say that elementary particles have “spin.” Imagining elementary particles as small spinning spheres is useful, but modern theories view this as a bit naive. Spin comes in a quantum amount. Some particles have whole integer values of quantum spin. That is, they have integer multiples (0, ±1, ±2, etc.) of the basic unit of spin. Physicists call these particles Bosons. Other particles have half integer (±1/2, ±3/2, etc.) amounts of spin, and are known as fermions. Bosons and fermions have very different properties. Physicists also noticed that elementary particles tended to have certain mathematical relationships between one another. Physicists eventually began to use group theory, a concept from abstract algebra, to classify and study elementary particles.

By the 1960s, physicists began to suspect that many elementary particles, such as protons and neutrons, were not so elementary after all, but consisted of even more elementary particles. Physicists called these more elementary particles quarks, after an enigmatic word in a James Joyce poem. According to the theory, there are six types of quarks. Many particles, such as protons and neutrons, consist of the combination of three quarks. The different combinations of quarks lead to different particles. Some of those combinations of quarks ought to produce particles that no one had yet seen, so these combinations amounted to predictions of new particles. Particles physicists were able to create these particles in experiments in particle accelerators, so the successful search for those predicted particles was confirmation of the underlying theory. Therefore, quark theory now is well established.

In recent years, particle physicists have in similar fashion developed string theory. Physicists have noticed that certain patterns among elementary particles can be explained easily if particles behave as tiny vibrating strings. These strings would require the existence of at least six additional dimensions of space. We already know that the universe has three normal spatial dimensions as well as the dimension of time, so these six extra dimensions bring the total number of dimensions to ten. The reason why we do not normally see the other six dimensions is that they are tightly curled up and hidden within the tiny particles themselves. At extremely high energies, the extra dimensions ought to manifest themselves. Therefore, particle physicists can predict what kind of behavior strings ought to exhibit when they accelerate particles to extremely high energies. The problem is that current particle accelerators are not nearly powerful enough to produce these effects. As theoretical physicists refine their theories and we build new, powerful particle accelerators, physicists expect that one day we can test whether string theory is true, but for now there is no experimental evidence for string theory.

The Size of Strings

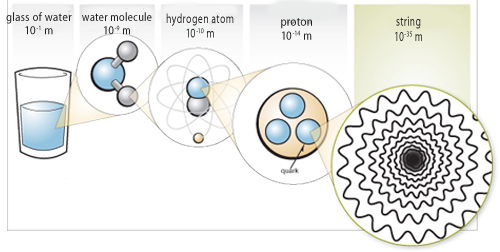
STRINGS—THE SMALLEST OBJECTS KNOWN TO PHYSICS
Looking at progressively smaller parts of a water molecule, we can glimpse the complexity God designed in all things.

We realize the illustration used deuterium, a rare isotope of hydrogen, to help convey the point.

Currently, most physicists think that string theory is a very promising idea. Assuming that string theory is true, there still remains the question as to which particular version of string theory is the correct one. You see, string theory is not a single theory but instead is a broad outline of a number of possible theories. Once we confirm string theory, we can constrain which version properly describes our world. If true, string theory could lead to new technologies. Furthermore, a proper view of elementary particles is important in many cosmological models, such as the big bang. This is because in the big-bang model, the early universe was hot enough to reveal the effects of string theory.

Conclusion

Modern physics is a product of the 20th century and relies upon twin pillars: quantum mechanics and general relativity. Both theories have tremendous experimental support. Christians ought not to view these theories with such great suspicion. True, some people have perverted or hijacked these theories to support some nonbiblical principles, but some wicked people have even perverted Scripture to support nonbiblical things. We ought to recognize that modern physics is a very robust, powerful theory that explains much. At the same time, the theory is very incomplete in some respects. In time, we ought to expect that some new theories will come along that will better explain the world than these theories do. However, we know that God’s Word does not change.

String theory has emerged in the 21st century as the next great idea in physics. Time will tell if string theory will live up to our expectations. What ought to be the reaction of Christians to this? We must be vigilant to investigate the amount of nonbiblical influences that may have crept into modern thinking, particularly in the interpretation of string theory (as with modern physics). However, we must be careful not to throw out the baby with the bath water. That is, can we reject the anti-Christian thinking that many have brought to the discussion? The answer is certainly yes. As with the question of origins, we must strive to interpret these things on our terms, guided by the Bible. Do the new theories adequately describe the world? Can we see the hand of the Creator in our new physics? Can we find meaning in our studies that brings glory to God? If we can answer yes to each of these questions, then these new theories ought not to be a problem for the Christian.