The views expressed in this paper are those of the writer(s) and are not necessarily those of the ARJ Editor or Answers in Genesis.
Abstract
In spite of numerous attempts over the last 60 years to determine the 87Rb half-life and decay constant, there is still no consensus on the absolute values. Even the more accurate determinations of the last 30 years have resulted in discrepancies. Determinations based on comparisons of ages of earth minerals and rocks give two different values of the 87Rb half-life and decay constant to the values using determinations based on comparison of ages of meteorites and lunar rocks. Yet the most recent direct counting and in-growth experimental determinations only agree with the most recent determinations based on comparison of the Rb-Sr ages of earth minerals and rocks with their U-Pb “gold standard” ages. This has resulted in suggested values of the 87Rb half-life and decay constant that are different from the two values of each previously championed in the literature. A similar discrepancy in determinations of the 176Lu half-life and decay constant has been recognized in the literature, as well as variations in the 238U/235U ratio so critical to the U-Pb “gold standard” against which the Rb-Sr ages have been calibrated. Since the 87Rb decay rate has thus not been accurately determined, the Rb-Sr dating method is certainly not absolute and therefore cannot be used to discredit the young-earth creationist timescale. However, further study is warranted to explore any potential significance in this discrepancy in half-lives and decay constants between earth materials, and meteorites and lunar rocks.
Keywords: radioisotope dating, decay constant, half-life, rubidium-87, 87Rb, β decay, direct counting, in-growth experiments, geological comparisons, discrepancies, meteorites, lunar rocks, earth minerals and rocks, 176Lu, U-Pb “gold standard”, 238U/235U.
Introduction
Radioisotope dating of rocks and meteorites is perhaps the most potent claimed proof for the old age of the earth and the solar system. The absolute ages provided by the radioisotope dating methods provide an apparent aura of certainty to the claimed millions and billions of years for formation of the earth’s rocks. Both the scientific community and the general public around the world (except perhaps in the USA) thus remain convinced of the earth’s claimed great antiquity.
The 1997–2005 RATE (Radioisotopes and the Age of The Earth) project successfully made progress in documenting some of the pitfalls in the radioisotope dating methods, and especially in demonstrating that radioisotope decay rates may not have always been constant at today’s measured rates (Vardiman, Snelling, and Chaffin 2000, 2005). Yet much research effort remains to be done to make further inroads into not only uncovering the flaws intrinsic to these long-age dating methods, but towards a robust understanding of radioisotopes and their decay during the earth’s history within a biblical creationist framework.
One crucial area the RATE project did not touch on was the issue of how reliable have been the determinations of the radioisotope decay rates, which are so crucial for calibrating these dating “clocks.” Accurate radioisotope age determinations depend on accurate determinations of the decay constants or half-lives of the respective parent isotopes. The reliability of the other two assumptions these absolute dating methods rely on, that is, the starting conditions and no contamination of closed systems, are unprovable. Yet these can be circumvented somewhat via the isochron technique, because it is independent of the starting conditions and is sensitive to revealing any contamination. Data points that do not fit on the isochron are simply ignored because their values are regarded as due to contamination. That this is common practice is illustrated with numerous examples from the literature by Faure and Mensing (2005) and Dickin (2005). On the other hand, it could be argued that this discarding of data points which do not fit the isochron is somewhat arbitrary and therefore is not good science, because it is merely assumed their “aberrant” values are due to contamination rather than that being proven to be so.
The aim of this contribution is to begin to document the methodology behind and history of determining the decay constants and half-lives of the parent radioisotopes used as the basis for the long-age dating methods. We need to explore just how accurate these determinations are, whether there really is consensus on standard values for the half-lives and decay constants, and just how independent and objective the standard values are from one another between the different methods. We begin here with rubidium-87 (87Rb), which is the basis for the Rb-Sr dating method.
Rubidium-87 Decay
The natural radioactivity of rubidium (Rb) was demonstrated in 1906, but it took more than thirty years for 87Rb to be identified as a naturally-occurring radioactive isotope (radioisotope) (Hahn, Strassman, and Walling 1937; Mattauch 1937). The feasibility of dating Rb-bearing minerals by the β-decay of 87Rb to 87Sr was first proposed by Hahn and Walling (1938), but the first determination by this method did not follow until a few years later (Hahn et al. 1943). However, the Rb-Sr method of radioisotope dating did not come into wide use until the 1950s, when mass spectrometers became available for routine isotopic analyses of solids (Nier 1940). At the same time the technology was developed to measure the concentrations of Rb and Sr by isotope dilution, combined with the separation of these elements by cation exchange chromatography. Faure and Powell (1972), Faure and Mensing (2005), and Dickin (2005) provide these and more details about the history of the development of the Rb-Sr dating method, and its theoretical basis and applicability.
Rubidium is a group-1 alkali metal. On the periodic table it is listed in the group IA column, which consists of Li, Na, K, Rb, Cs, and Fr. The ionic radius of Rb+ is 1.48 Å, which is sufficiently similar to that of K+ (1.33 Å) to allow it to substitute for K+ in all K-bearing minerals. Rubidium is an element that does not form minerals in which it is a major constituent. Instead, Rb is a dispersed element in trace amounts in other minerals. For example, it occurs in easily detectable amounts in common K-bearing minerals, such as the micas (muscovite, biotite, phlogopite and lepidolite), K-feldspars (orthoclase and microcline), certain clay minerals, and the evaporite (precipitite) minerals sylvite and carnallite.
Rubidium has two naturally-occurring isotopes 85Rb and 87Rb, whose abundances are 72.17% and 27.83% respectively (Dickin 2005; Faure and Mensing 2005). Rubidium-87 is radioactive and decays to stable 87Sr:-
87Rb → 87Sr + β¯ + ⊽ + Q
A negative β-particle (β¯) and an anti-neutrino (⊽) are both emitted in this process. The decay energy (Q) is shared as kinetic energy by these two particles. Fortunately this β-decay of 87Rb is a single-step process. In effect, it can be regarded as the transformation of a neutron within the 87Rb nucleus into a proton and an electron, the latter then being expelled as a negative β-particle. The relative simplicity of this decay step therefore makes measuring the decay rate of 87Rb relatively straight forward.
There are two parameters by which the decay rate is measured and expressed, namely, the decay constant (λ) and the half-life (t½). The latter is the time it takes for half of a given number of the parent radionuclide atoms to decay. The two quantities can be almost used interchangeably, because they are related by the equation:-
t½ = ln 2 λ = 0.693 λ
Determination Methods
Three approaches have so far been followed to determine the β-decay constant and half-life of the long-lived radioactive 87Rb.
Direct counting
In this technique, the beta (β) activity of 87Rb is counted in a source material, and divided by the total number of radioactive atoms in the known quantity of Rb, based on Avogadro’s number and the isotopic abundance of 87Rb. Among the difficulties of this approach are the self-shielding of finite-thickness solid samples, the low specific activities, imprecise knowledge of the isotopic composition of the parent Rb, the detection of very low-energy decays, and problems with detector efficiencies and geometry factors (Begemann et al. 2001).
The low decay energy for this 87Rb β-decay transformation (0.275 MeV) has always caused problems in the accurate determination of the 87Rb decay constant (Dickin 2005; Faure and Mensing 2005). Because the decay energy is divided between the β-particles and the anti-neutrinos, the β-particles have a smooth distribution of kinetic energy from the total energy down to zero. When attempting to determine the decay constant by direct counting the low-energy β-particles cause great problems because they may be absorbed by surrounding Rb atoms before they ever reach the detector. For example, in a thick (>1 µm) solid Rb sample, attenuation is so severe that a false frequency maximum is generated at about 10 keV.
One way this attenuation problem has been avoided is to use a photo-multiplier with a liquid scintillation solution doped with Rb. The β-particles will be absorbed by molecules of the scintillator (emitting flashes of light) before they can be absorbed by other Rb atoms. The major problem with this method is that a low-energy cut-off at about 10 keV must be applied to avoid the high background noise associated with liquid scintillation (Dickin 2005). The consequent extrapolation of count-rate curves down to zero energy leads to a large uncertainty in the result. Hence this method has given values for the 87Rb half-life from 47.0 ± 1.0 Byr (Flynn and Glendenin 1959) to 52.1 ± 1.5 Byr (Brinkman, Aten, and Veenboer 1965).
Another approach to direct counting is to make measurements with progressively thinner solid Rb sources using a proportional counter. The results are then extrapolated to a theoretical source of zero thickness to remove the effect of self-absorption. The proportional counter has a much lower noise level, so the energy cut-off can be set as low as 0.185 keV. Rb films with thicknesses down to 1 µm were measured by Neumann and Huster (1974), and extrapolated to zero thickness by Neumann and Huster (1976) to derive a 87Rb half-life of 48.8 ± 0.8 Byr (equivalent to a decay constant of 1.42 × 10-11 yr-1).
Judged from the fact that many of the direct counting experiments have yielded results that are not compatible with one another within the stated uncertainties (see below), it would appear that not all the measurement uncertainties are accounted for, and therefore the stated uncertainties are unrealistically small. Many of such experiments are plagued by unrecognized systematic errors (Begemann et al. 2001). As the nature of these errors is obscure, it is not straightforward to decide which of the, often mutually exclusive, results of such direct counting experiments is closest to the true value. Furthermore, the presence of unknown systematic biases makes any averaging dangerous. It is possible that reliable results of careful workers, listing realistic uncertainties, will not be given the weights they deserve—this aside from the question of whether it makes sense to average numbers that by far do not agree within the stated uncertainties.
In-Growth Experiments
An alternative approach to determining the 87Rb decay constant and half-life is to measure the amount of 87Sr produced by the decay of a known quantity of 87Rb in the laboratory over a known period of time. This method was first attempted by McMullen, Fritze, and Tomlinson (1966) on an Rb sample that was purified in 1956, and was repeated on the same sample batch by Davis et al. (1977). Unfortunately, McMullen, Fritze, and Tomlinson (1996) omitted to measure the small but significant level of residual 87Sr present in their Rb sample before they put it away on the shelf. Hence, the accuracy of their determination was compromised. However, this problem contributed less than 1% uncertainty to the later determination of Davis et al. (1977). Their proposed value for the 87Rb half-life of 48.9 ± 0.4 Byr, equivalent to a decay constant of 1.42 × 10-11 yr-1, would thus seem to support the value of Neumann and Huster (1976) obtained by direct counting.
This technique thus relies on measuring the β-decay product 87Sr of a well-known amount of a radioactive 87Rb accumulated over a well-defined period of time. Where feasible, this is the most straightforward technique (Begemann et al. 2001). In-growth measurement overcomes the problems encountered with direct counting of large fractions of low-energy 87Rb-emitted β-particles. It also comprises the direct 87Sr product of any radiation-less decays (which otherwise cannot be measured at all).
Among the drawbacks of this approach is that the method is obviously not instantaneous. The experiment must be started long before the first results can be obtained because long periods of time (typically decades) are required for sufficiently large amounts of the decay products to accumulate. In-growth experiments further require an accurate determination of the ratio of the two chemical elements (parent/daughter, 87Rb/87Sr) as well as an accurate determination of the isotopic composition of parent and daughter elements Rb and Sr at the start of the accumulation (Begemann et al. 2001).
Geological comparisons of methods
The third approach to the determination of the 87Rb decay constant (and half-life) has been to date geological samples whose ages have also been measured by other methods with presumably more reliable decay constants (Dickin 2005; Faure and Mensing 2005). This method has the disadvantage that it involves geological uncertainties, such as whether all isotopic systems closed at the same time and remained closed. However, it is claimed to still provide a useful check on the direct laboratory determinations. In this respect it is worth noting that Pinson et al. (1963) proposed a 87Rb half-life of 48.8 Byr on the basis of Rb-Sr dating of stony meteorites (chondrites) that had also been U-Pb dated, well before Neumann and Huster (1974, 1976) arrived at the essentially the same 87Rb half-life value via direct counting.
This approach entails multi-chronometric dating of a rock and cross-calibration of different radioisotopic age systems by adjusting the decay constant of one system so as to force agreement with the age obtained via another dating system (Begemann et al. 2001). In essence, because the half-life of 238U is the most accurately known of all relevant radionuclides, this usually amounts to expressing ages in units of the half-life of 238U.
Results of the Rubidium-87 Decay Determinations
During the last 60 years numerous determinations of the 87Rb decay constant and half-life have been made using these three methods. The results are listed with details in Table 1. The year of the determination versus the value of the decay constant is plotted in Fig. 1, and the year of the determination versus the value of the half-life is plotted in Fig. 2. In each diagram the data points plotted have been color-coded the same to differentiate the values as determined by the three approaches that have been used—direct counting, in-growth experiments, and geological comparisons with other radioisotope dating methods.
Table 1. Determinations of the 87Rb decay rate expressed in terms of the half-life and decay constant using direct counting, in-growth experiments and comparisons of radioisotope ages.
| Determination of the 87Rb Decay Rate | ||||||
|---|---|---|---|---|---|---|
| Date | Half-Life (x 1010 yr) |
Decay Constant (x 10-11yr-1) |
Method | Source | ||
| 1948 | 6.0 | ±0.6 | 1.155 | ±0.2 | Liquid scintillation direct/absolute counting | Haxel, Houtermans, and Kemmerich 1948 |
| 1951 | 6.15 | ±0.30 | 1.127 | ±0.09 | Liquid scintillation/spectrometer direct counting | Curran, Dixon, and Wilson 1951 |
| 1952 | 5.90 | ±0.30 | 1.175 | ±0.09 | Liquid scintillation/spectrometer direct counting | Lewis 1952 |
| 1954 | 6.2 | ±0.3 | 1.118 | ±0.09 | Spectrometer direct counting | MacGregor and Wiedenbeck 1954 |
| 1955 | 4.3 | ±0.25 | 1.612 | ±0.07 | Scintillation/spectrometer direct counting | Geese-Bähnisch 1955 |
| 1956 | 5.0 | ±0.2 | 1.39 | ±0.06 | U-Pb age comparison of minerals | Aldrich et al. 1956 |
| 1959 | 4.70 | ±0.10 | 1.475 | ±0.031 | Liquid scintillation direct/absolute counting | Flynn and Glendenin 1959 |
| 1961 | 5.25 | ±0.10 | 1.32 | ±0.03 | Scintillation direct counting | McNair and Wilson 1961 |
| 1961 | 5.82 | ±0.1 | 1.191 | ±0.03 | Scintillation/spectrometer direct counting | Egelkraut and Leutz 1961 |
| 1961 | 5.53 | ±0.10 | 1.253 | ±0.03 | Scintillation/spectrometer direct counting | Beard and Kelly 1961 |
| 1962 | 5.80 | ±0.12 | 1.195 | ±0.04 | Scintillation/spectrometer direct counting | Leutz, Wenninger, and Ziegler 1962 |
| 1963 | 4.88 | 1.420 | Comparison of Rb-Sr and other ages for stony meteorites | Pinson et al 1963 | ||
| 1964 | 4.77 | ±0.10 | 1.453 | ±0.03 | Liquid scintillation direct/absolute counting | Kovách 1964 |
| 1965 | 5.21 | ±0.15 | 1.33 | ±0.05 | Liquid scintillation direct/absolute counting | Brinkman, Aten, and Veenboer 1965 |
| 1966 | 4.72 | ±0.04 | 1.468 | ±0.012 | In growth experiment by mass spectrometry | McMullen, Fritze, and Tomlinson 1966 |
| 1974, 1976 | 4.88 | ±0.06/0.10 | 1.420 | ±0.030/0.017 | Absolute counting experiments | Neumann and Huster 1974, 1976 |
| 1977 | 4.89 | ±0.04 | 1.419 | ±0.012 | In growth experiment and counting | Davis et al. 1977 |
| 1977 | 4.88 | ±0.03 | 1.420 | ±0.010 | K-Ar and U-Pb age comparisons of minerals | Steiger and Jager 1977 |
| 1982 | 4.94 | ±0.03 | 1.402 | ±0.008 | U-Th-Pb age comparison with H, E, and LL chondrites | Minster. Birck, and Allègre 1982 |
| 1982 | 4.88 | ±0.03 | 1.420 | ±0.010 | K-Ar comparison with SE Australian granites | Williams et al 1982 |
| 1985 | 4.94 | ±0.04 | 1.402 | ±0.011 | Sm-Nd + K-Ar age comparisons of lunar rocks | Shih et al 1985 |
| 2001 | 4.94 | ±0.03 | 1.402 | ±0.008 | Comparisons of all methods | Begemann et al 2001 |
| 2002 | 4.95 | ±0.02 | 1.400 | ±0.007 | Comparison of Rb-Sr and U-Th-Pb mineral ages | Amelin and Zaitsev 2002 |
| 2003 | 4.967 | ±0.032 | 1.395 | ±0.009 | Liquid scintillation direct/absolute counting | Kossert 2003 |
| 2011 | 4.975 | ±0.010 | 1.393 | ±0.004 | Comparison of Rb-Sr and U-Th-Pb mineral ages | Nebel, Scherer, and Mezger 2011 |
| 2012 | 4.962 | ±0.008 | 1.397 | ±0.0015 | In growth experiment by mass spectrometry | Rotenberg et al 2012 |
Discussion
The values for the 87Rb decay constant used in Rb-Sr age calculations for rocks over the last sixty years have varied between 1.47 × 10-11 yr-1 and 1.39 × 10-11 yr-1 (equivalent to half-lives of 46.8 Byr and 50.0 Byr respectively). The most commonly used value of 1.42 × 10-11 yr-1 (48.8 Byr) was adopted by international convention (Steiger and Jäger 1977). Two papers reporting direct determinations of the 87Rb decay constant and half-life that had appeared before preparation of the report of the 1976 IUGS Subcommission on Geochronology were cited by that 1976 meeting of this Subcommission (Steiger and Jäger 1977) as influencing their recommendation of the 87Rb decay constant of 1.42 × 10-11 yr-1, corresponding to a half-life of 48.8 Byr. These were Neumann and Huster (1974), who reported measuring the specific activity of thin sources of rubidium chloride (RbCl) using a 4π proportional counter to obtain a 87Rb half-life of 4.88 + 0.06 / −0.10 Byr, and Davis et al. (1977), who reported continuing the direct mass spectrometric “in-growth” experiment initiated by McMullen, Fritze, and Tomlinson (1966) to obtain a 87Rb half-life of 4.89 ± 0.04 Byr.
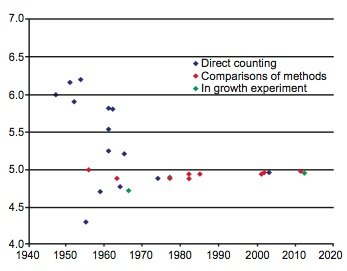
Fig. 1. Plot of each 87Rb half-life determination versus the year of its determination, color-coded according to the method of its determination.
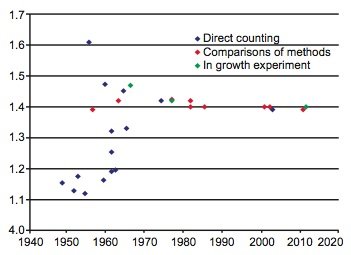
Fig. 2. Plot of each 87Rb decay constant determination versus the year of its determination, color-coded according to the method of its determination.
A third line of evidence cited by Steiger and Jäger (1977) as influencing their choice of the recommended value of the 87Rb decay constant was a comparison of Rb-Sr ages with K-Ar ages presented by Tetley et al. (1976). However, it was later noted that in Tetley et al. (1976) there was a discernible tendency towards higher calculated 87Rb decay constant values for lower K-Ar ages, as would be expected if some of the calculated K-Ar ages were too low due to Ar loss (Begemann et al. 2001). Consideration of the more extensive data set of Williams et al. (1982), which contained the data of Tetley et al. (1976) as a subset, suggested that the average 87Rb constant value provided by this comparison may have been biased high by 1 to 2% 40Ar loss from many of the analyzed samples. This loss may have been due to alteration, as all micas show sub-stoichiometric K concentrations. Shih et al. (1985) compared Rb-Sr ages of lunar KREEP basalts to 39Ar-40Ar ages calculated with the 40K decay parameters recommended by Steiger and Jäger (1977), and found the best agreement for the 87Rb decay constant was 1.402 ± 0.011 × 10-11 yr-1 (corresponding to a half-life of 49.4 Byr). Although Shih et al. (1985) compared significantly fewer ages, according to Begemann et al. (2001) the correction for 40Ar loss inherent in the 39Ar-40Ar technique probably made the value of the 87Rb decay constant they obtained more reliable than that derived by Tetley et al. (1976). Note, however, that the large uncertainties in the 40K decay constants of Steiger and Jäger (1977) undermine the usefulness of any normalization to this system (Begemann et al. 2001).
Thus the value recommended by the Subcommission did not gain universal acceptance. For example, Minster, Birck, and Allègre (1982) summarized the Rb-Sr data for chondrites (stony meteorites) from their Paris laboratory, and found the best agreement between the whole-rock Rb-Sr age of those chondrites and their average U-Pb ages of 4.555 ± 0.010 Ga was for a 87Rb decay constant of 1.402 ± 0.008 × 10-11 yr-1 (equivalent to a half-life of 49.4 Byr). Conversely, the whole-rock isochron for the chondrites yielded an initial 87Sr/86Sr ratio of 0.69885 ± 0.00010 and an age of 4.498 ± 0.015 Ga for an 87Rb decay constant of 1.42 × 10-11 yr-1 (corresponding to a half-life of 48.8 Byr). Since that initial 87Sr/86Sr ratio is similar to other estimates of the initial 87Sr/86Sr for the solar system (for example, BABI, Papanastassiou and Wasserburg 1969), Begemann et al. (2001) concluded there was no reason to suspect the Rb-Sr isotopic systematics of these chondrites had been reset to an age lower than the U-Pb age.
Thus Begemann et al. (2001), in issuing a call for new revised values, contended that therefore it was totally reasonable to expect the Rb-Sr and U-Pb ages for these chondrites to be the same. Thus they argued for the 87Rb decay constant of 1.402 ± 0.008 × 10-11 yr-1 and the equivalent half-life of 49.4 Byr proposed by Minster, Birck, and Allègre (1982) to be the new values. They also pointed out that the most commonly encountered bias factors in determining the 87Rb decay constant all operated in a single direction, increasing the apparent value of the 87Rb decay constant. Begemann et al. (2001) thus concluded that there was therefore a significant probability that the value recommended by Steiger and Jäger (1977) was too high by 1 to 2%. Furthermore, they suggested that investigators seeking a precise comparison of Rb-Sr ages to those determined by other methods should consider the effect on the comparison of using an 87Rb decay constant of 1.402 × 10-11 yr-1, as suggested originally by Minster, Birck, and Allègre (1982), and recommend that the value of the 87Rb decay constant should be re-determined with improved accuracy.
This recommendation for new determinations of the 87Rb decay constant and half-life with improved accuracy was immediately pursued by Kossert (2003) by liquid scintillation direct counting, and later by Rotenberg et al. (2012) with in-growth experiments (see table 1). However, rather than confirming the values Begemann et al. (2001) preferred, Kossert (2003) found from his measurements that the 87Rb half-life should be 49.67 ± 0.32 Byr (equivalent to a decay constant of 1.395 ± 0.009 × 10-11 yr-1). Similarly, Rotenberg et al. (2012) concluded from their measurements of the 87Sr accumulation in RbClO4 salt over 32 years that the 87Rb half-life should be 49.624 +0.065/-0.095 Byr (equivalent to a decay constant of 1.3968 +0.0027/-0.0018 × 10-11 yr-1). Furthermore, two more recent studies reported comparisons between Rb-Sr and U-Pb ages for minerals (Amelin and Zaitsev 2002) and rocks (Nebel, Scherer, and Mezger 2011), and both also suggested lower values for the 87Rb half-life and decay constant than those championed by Begemann et al. (2001) (see table 1).
In order to more clearly see the differences between the determinations made in the last 30 years by all three methods, the scatter of the early years of determinations was ignored and only the last 30 years’ results were plotted using the same color coding for the different methods, the half-life determinations in Fig. 3 and the decay constant determinations in Fig. 4. For the purpose of this discussion, the two competing values for the half-life (48.8 and 49.4 Byr) and decay constant (1.42 × 10-11 yr-1 and 1.402 × 10-11 yr-1 respectively) have been marked on the diagrams by vertical dashed lines.
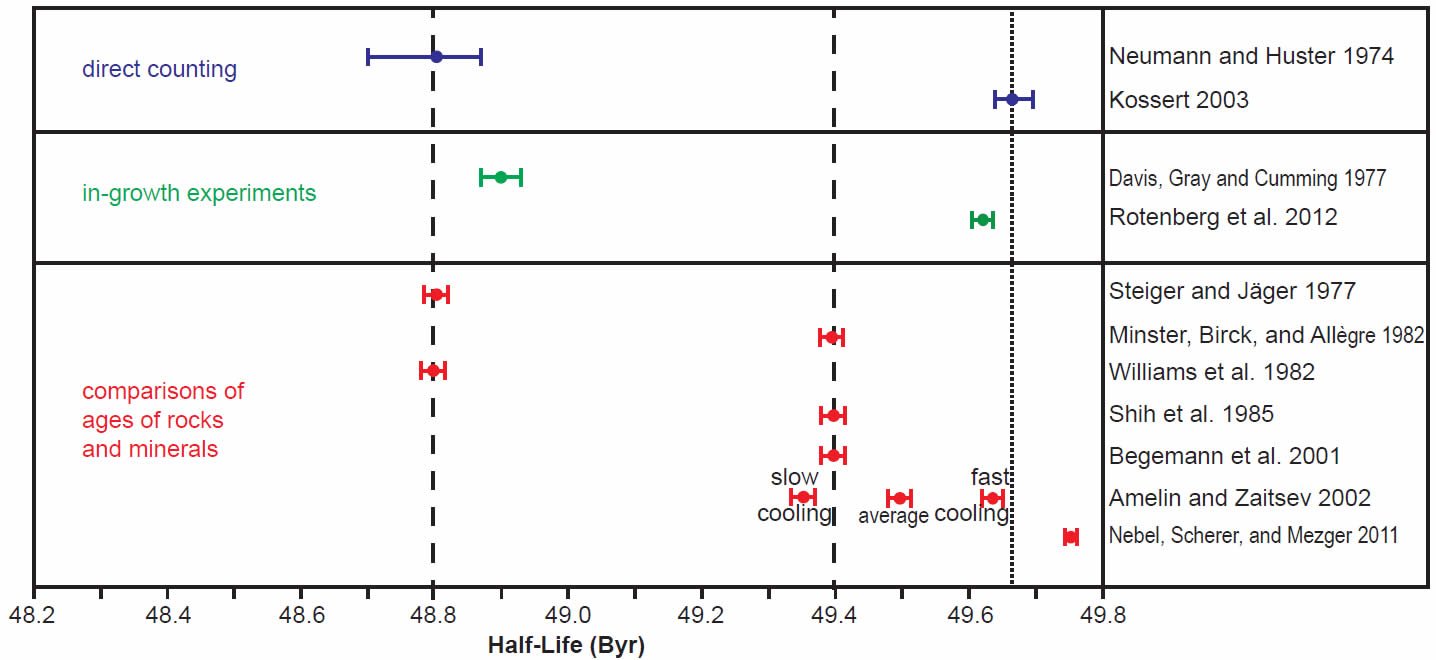
Fig. 3. Comparison of the 87Rb half-life determinations obtained in the last 30 years, grouped and color-coded according to the methods of determination. The vertical dashed lines represent the two competing values for the 87Rb half-life in the literature, while the vertical dotted line represents the proposed new best value based on the most recent determinations, as discussed in the text.
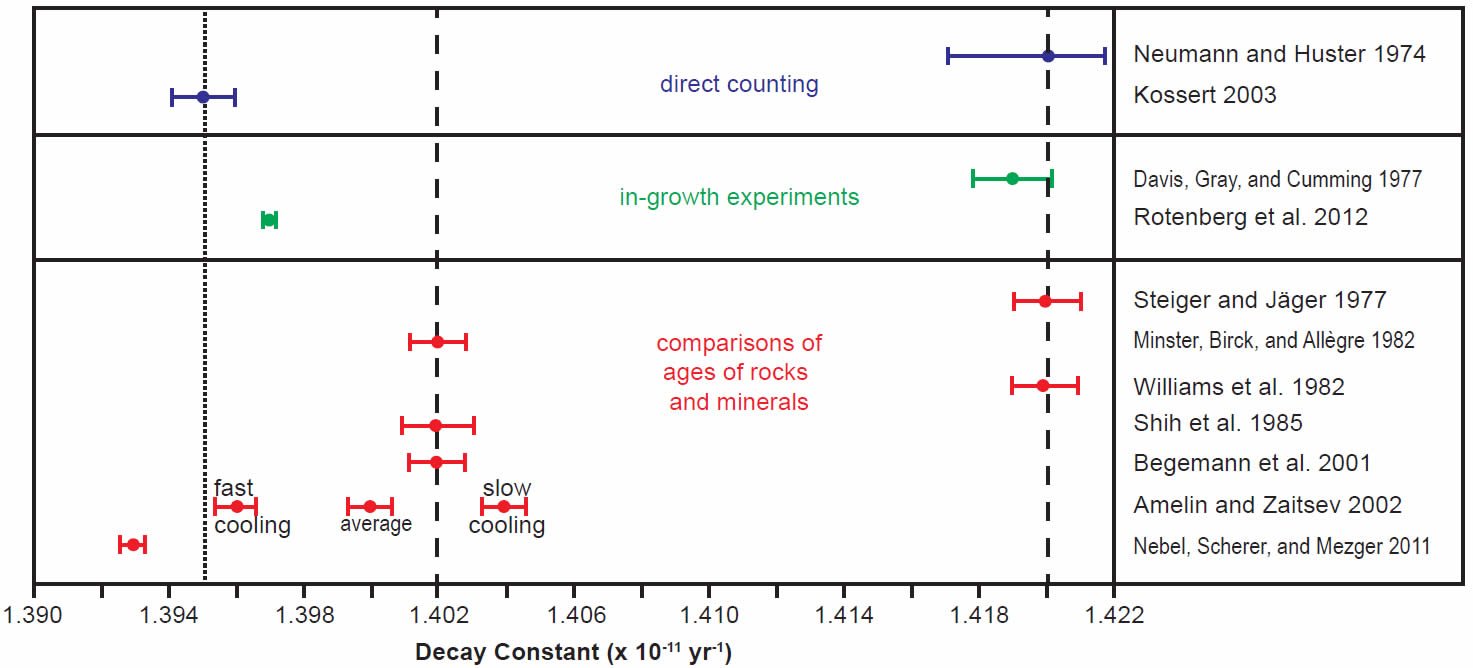
Fig. 4. Comparison of the 87Rb decay constant determinations obtained in the last 30 years, grouped and color-coded according to the methods of determination. The vertical dashed lines represent the two competing values for the 87Rb decay constant in the literature, while the vertical dotted line represents the proposed new best value based on the most recent determinations, as discussed in the text.
The grouping of determinations around a half-life of 48.8 Byr corresponding to a decay constant of 1.42 × 10-11 yr-1 includes the earlier Neumann and Huster (1974, 1976) direct counting determination and Davis et al. (1977) in-growth experiment, and the earlier Steiger and Jäger (1977) and Williams et al. (1982) geological comparisons of the whole-rock Rb-Sr and K-Ar ages of rapidly cooled igneous rocks and granites (figs 3 and 4). In stark contrast, the grouping of determinations around a half-life of 49.4 Byr corresponding to a decay constant of 1.402 × 10-11 yr-1 championed by Begemann et al. (2001) is only supported by the earlier comparison of ages studies of Minster, Birck, and Allègre (1982) on Rb-Sr and U-Pb ages of chondrites (stony meteorites) and Shih et al. (1985) on Rb-Sr and Ar-Ar ages of lunar KREEP basalts (figs 3 and 4).
What is also evident in Figs 3 and 4 is that the most recent half-life and decay constant determinations by Kossert (2003) by direct counting and Rotenberg et al. (2012) by in-growth experiments do not support the half-life of 49.4 Byr and decay constant of 1.402 × 10-11 yr-1. And neither do the most recent geological comparisons of ages studies by Amelin and Zaitsev (2002) and Nebel, Scherer, and Mezger (2011). This observation was not lost on Nebel, Scherer, and Mezger (2011) and Rotenberg et al. (2012) either, who thus both championed a different longer half-life and lower decay constant, which are shown in their own compilation diagrams in Figs 5 and 6 respectively.
Indeed, when Amelin and Zaitsev’s (2002) fast and slow cooling determinations are separated from the averaging of them shown in table 1, and plotted in Figs 3 and 4 separately, as they are by Rotenberg et al. (2012) (fig. 6), the slow cooling determinations plot with the Begemann et al. (2001) championed half-life and decay constant, whereas the fast cooling determinations plot with the most recent determinations by Kossert (2003) by direct counting, Rotenberg et al. (2012) by in-growth experiments, and Nebel, Scherer, and Mezger (2011) by comparisons of geological ages. This grouping is shown in Figs 3 and 4 by dotted lines corresponding to a half-life of 49.67 ± 0.05 Byr and a decay constant of 1.395 ± 0.005 × 10-11 yr-1.
But there is more here in these data than what has been observed by Nebel, Scherer and Mezger (2011) and Rotenberg et al. (2012). It could be significant that the comparisons of geological ages performed by Amelin and Zaitsev (2002) and Nebel, Scherer, and Mezger (2011) were based on minerals (baddeleyite, zircon, apatite, phlogopite, biotite, feldspar, and amphibole) from earth rocks (phoscorites, carbonatites, and syenites) using U-Pb ages as the “gold standard,” whereas those of Minster, Birck, and Allègre (1982) and Shih et al. (1985) were based on chondrites (stony meteorites) and lunar KREEP basalts respectively. Indeed, this same observation that there are differences in the half-life and decay constant between determinations using earth materials and determinations using meteorites has already been documented for 176Lu by Albarède et al. (2006). They found that using the earth-based 176Lu decay constant the Lu-Hf ages of chondrites were consistently 4% higher than their U-Pb ages, so the reconciliation of the Lu-Hf and U-Pb ages required using a different meteorite-based 176Lu decay constant. Ironically, but significantly, Albarède et al. (2006) proposed that this discrepancy between decay constants could be because of accelerated 176Lu decay during the first few million years of the existence of the solar nebula due to irradiation of the 176Lu by γ -rays emitted by one or more supernova(e) exploding in the vicinity of the solar nebula.
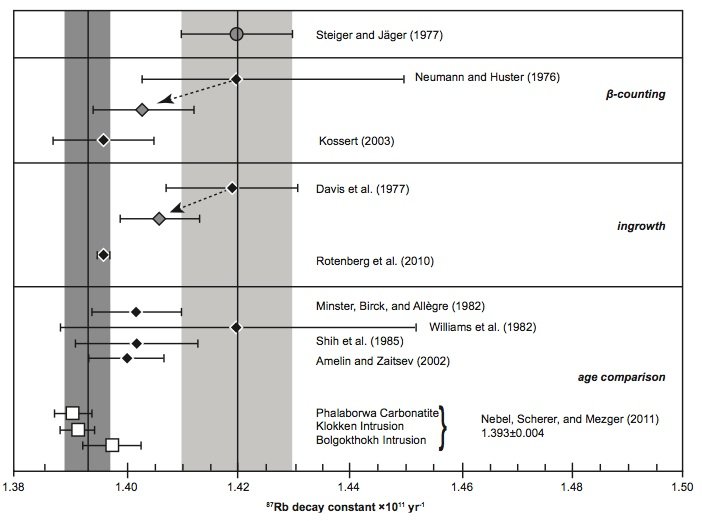
Fig. 5. Comparison of the 87Rb decay constant determinations of the last thirty years according to Nebel, Scherer, and Mezger (2011).
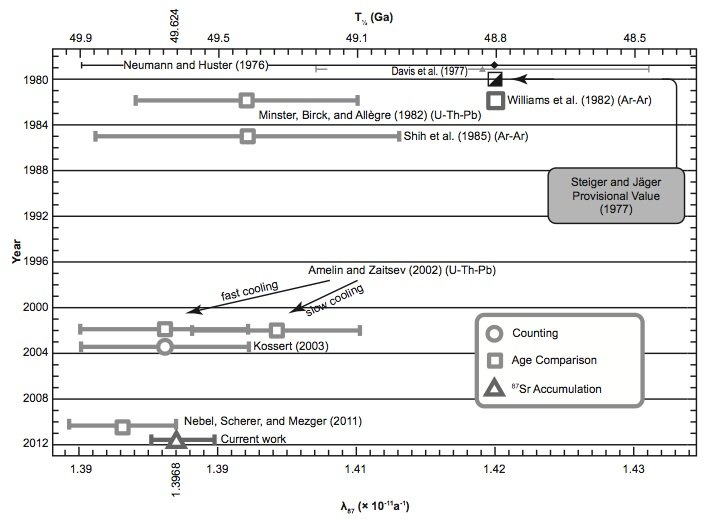
Fig. 6. Comparison of the 87Rb half-life and decay constant determinations of the last 30 years according to Rotenberg et al. (2012).
In the related context of nucleosynthesis of the elements inside stars, Zhao and Käppeler (1990) found the absorption cross-section to produce 176Lu to be small and hence found problems explaining their data. They concluded that to reestablish the 176Lu clock for determining the age of the s-process elements would, in any case, require a quantitative description of all processes feeding the ground state as well as a reliable model for the s-process environment, in particular for the temperatures to which 176Lu was exposed during its production and ever since. However, even though these effects of ionization on the nuclear half-lives can be enhanced inside stars due to the extreme ionization prevalent there, such contexts are not relevant in the creationist framework for the history of the earth and the universe. The earth and its rocks, and their contained elements and isotopes, were all created before the stars, the moon, and the asteroids from which the meteorites subsequently came. And then in their history since their creation neither the earth nor the asteroids have been subjected to the intense ionization inside stars.
There would thus appear to be similar discrepancies in the 87Rb and 176Lu decay constants and half-lives between determinations using earth materials and determinations using meteorites and lunar rocks. This is the first time this discrepancy has been recognized for the 87Rb half-life and decay constant. It also may be relevant that both 87Rb and 176Lu decay via the same single-step β-decay process, both producing anti-neutrinos and decay energy. Such discrepancies are a conundrum to conventional wisdom, but may provide new insights for creationist thinking. Furthermore, even the U-Pb “gold standard” has come under similar scrutiny in the last decade. The U-Pb method depends on the crucial 238U/235U ratio, but discrepancies and variations have been found between the 238U/235U ratio in U-bearing earth-based (terrestrial) minerals and rocks and the 238U/235U ratio in meteorites (Brennecka and Wadhwa 2012; Hiess et al 2012). The potential significance of these discrepancies and variations from a creationist perspective awaits further study, especially in the context of examinations of the determinations of the 176Lu, 238U, and 235U decay constants and half-lives.
Nevertheless, it is still obvious that in spite of this discrepancy, the most recent earth-based direct counting and in-growth experimental determinations of the 87Rb half-life and decay constant (Kossert 2003; Rotenberg et al. 2012) coincide with the 87Rb half-life and decay constant determined via comparisons of Rb-Sr and U-Pb ages of minerals from earth rocks (Amelin and Zaitsev 2002; Nebel, Scherer, and Mezger 2011), and not with the currently accepted 87Rb half-life and decay constant (Begemann et al. 2001). And the fact that there are also variations in the crucial 238U/235U ratio in earth minerals and rocks on which the U-Pb dating “gold standard” depends, which is so obviously used to calibrate the 87Rb half-life and decay constant, only underscores that these radioisotope methods cannot provide the absolute invariable “dates” they are so confidently proclaimed to provide. It is thus surely significant that the Rb-Sr method has not been used to provide any of the absolute dates for the GSSPs (global boundary stratotype sections and points) or “golden spikes” in the official and approved Geologic Time Scale of the International Union of Geological Sciences (IUGS) (International Union of Geological Sciences 2014; Schmitz 2012a, b).
Not only does the potential significance of these discrepancies in the 87Rb and 176Lu half-lives and decay constants and the variations in the 238U/235U ratio need further investigating, but also the effect on the Rb-Sr ages of meteorites in relation to their ages derived by the other radioisotope dating systems, when those Rb-Sr ages are recalculated using the revised 87Rb half-life and decay constant proposed here (49.67 ± 0.05 Byr and 1.395 ± 0.005 × 10-11 yr-1). It is possible that such systematically recalculated Rb-Sr ages may introduce a systematic difference between the meteorites’ Rb-Sr age ages relative to their ages derived by the other radioisotope dating systems. However, since the changes in the meteorites’ Rb-Sr ages introduced by such systematic recalculations would only amount to an increase of about 0.6–1.8%, the effect in comparison to their ages derived by the other radioisotope dating systems would likely be negligible, especially given the error margins in many meteorite age determinations. Thus such recalculated meteorite Rb-Sr ages would not likely reveal any of the trends that would evidence a past accelerated radioisotope decay event (Vardiman, Snelling, and Chaffin 2005). This is confirmed by Snelling (2014a, b), who has shown that at least for the chondrites (the carbonaceous, ordinary and enstatite stony meteorites) there are no indications of any systematic differences in their isochron ages with respect to their ages derived by the other radioisotope dating systems that would evidence a past accelerated radioisotope decay event. Instead, their Rb-Sr ages either occasionally agree with the dominant strong clusters of Pb-Pb ages, or more often are widely scattered either side of those clusters.
Finally, it would remain prudent to be very careful with these geological comparison methods for two reasons. First, there are significant flaws in the basic assumptions that all of them embrace. Second, the U-Pb method relies primarily on α decay whereas the Rb-Sr method relies on β decay. As observed by both Austin (2005) and Snelling (2005), these different decay modes seem to yield different ages for earth rocks using the same samples with essentially the same methodology. Furthermore, as described earlier, direct counting by liquid scintillation is fraught with pitfalls when measuring low-level β emitters.
Conclusions
There have been numerous attempts to determine the 87Rb half-life and decay constant in the last sixty years by three methods—direct counting of β-particles, in-growth experiments in which the daughter 87Sr accumulated over a given time is measured, and comparisons of Rb-Sr ages of earth minerals and rocks, lunar rocks, and meteorites with ages derived by other radioisotope systems, especially U-Pb. The estimates of the 87Rb half-life are really consistent since 1985. Going back in time the first inconsistent measurement was by comparison of radioisotope ages for some southeast Australian granites, and that was just barely inconsistent. Thus the data seem to be simply paralleling the improvements in measurement technologies with poorly estimated errors.
However, with the improved accuracy in such determinations in the last thirty years, a discrepancy has been revealed which has been debated in the literature, but with no attempted explanation as to the cause. The discrepancy is between the 87Rb half-life and decay constant (48.8 Byr and 1.42 x 10-11 yr-1 respectively) determined by comparing the Rb-Sr ages of earth rocks against their K-Ar and Ar-Ar ages, and the 87Rb half-life and decay constant (49.4 Byr and 1.402 × 10-11 yr-1 respectively) determined by comparing the Rb-Sr ages of meteorites and lunar rocks with their U-Pb and Ar-Ar ages respectively. The direct counting and in-growth experimental determinations of the 1970s only agree with the 87Rb half-life of 48.8 Byr determined by comparing the Rb-Sr ages of earth rocks against their K-Ar and Ar-Ar ages. Yet the 87Rb half-life of 49.4 Byr determined by comparing the Rb-Sr ages of meteorites and lunar rocks with their U-Pb and Ar-Ar ages respectively have been championed since the mid-1980s as the best to use in calculating Rb-Sr ages.
Nevertheless, now a further discrepancy has been revealed in the last decade by the most recent 87Rb half-life determinations. Both new determinations by direct counting and in-growth experiments do not agree with either of the two previously derived 87Rb half-lives and decay constants. Instead, they only agree with the two new determinations derived from comparing Rb-Sr ages of further earth minerals and rocks with their U-Pb ages, the so-called “gold standard.” It is thus proposed here that these new data define a new and better estimate of the 87Rb half-life and decay constant of 49.67 ± 0.05 Byr and 1.395 ± 0.005 × 10-11 yr-1 respectively. Furthermore, this highlights the disparity between determinations using earth materials and extraterrestrial materials, which is similar to the already documented similar disparity in determinations of the 176Lu half-life and decay constant. These discrepancies only serve to highlight that the Rb-Sr dating method cannot be absolute when the 87Rb decay rate has not been accurately determined. When it is calibrated against the U-Pb “gold standard” with its own uncertainties in the critical 238U/235U ratio it still cannot be regarded as absolute. Therefore, Rb-Sr dating cannot be used to discredit the young-earth creationist timescale. However, further study is needed to explore whether this discrepancy between earth and extraterrestrial materials has any significance.
References
Albarède, F., E. E. Scherer, J. Blichert-Toft, M. Rosing, A. Simionovici, and M. Bizzarro. 2006. γ-ray irradiation in the early Solar System and the conundrum of the 176Lu decay constant. Geochimica et Cosmochimica Acta 70, no. 5:1261–1270.
Aldrich, L. T., G. W. Wetherill, G. R. Tilton, and G. L. Davis. 1956. Half-life of Rb87. Physical Review 103, no. 4:1045–1047.
Amelin, Y. and A. N. Zaitsev. 2002. Precise geochronology of phoscorites and carbonatites: The critical role of U-series disequilibrium in age interpretations. Geochimica et Cosmochimica Acta 66, no. 13:2399–2419.
Austin, S. A. 2005. Do radioisotope clocks need repair? Testing the assumptions of isochron dating using K-Ar, Rb-Sr, Sm-Nd, and Pb-Pb isotopes. In Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E.F. Chaffin, pp. 325–392. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society.
Beard, G. B., and W. H. Kelly. 1961. “Self-scintillation” study of the beta decay of Rb87. Nuclear Physics 28, no. 4:570–577.
Begemann, F., K. R. Ludwig, G. W. Lugmair, K. Min, L. E. Nyquist, P. J. Patchett, P. R. Renne, C.-Y. Shih, I. M. Villa, and R. J. Walker. 2001. Call for an improved set of decay constants for geochronological use. Geochimica et Cosmochimica Acta 65, no. 1:111–121.
Brennecka, G. A., and M. Wadhwa. 2012. Uranium isotope compositions of the basaltic angrite meteorites and the chronological implications for the early Solar System. Proceedings of the National Academy of Sciences USA 109, no. 24:9299–9303.
Brinkman, G. A., A. H. W. Aten Jr., and J. Th. Veenboer. 1965. Natural radioactivity of K-40, Rb-87 and Lu-176. Physica 31, no. 8:1305–1319.
Curran, S. C., D. Dixon, and H. W. Wilson. 1951. The natural radioactivity of rubidium. Physical Review 84, no. 1:151–152.
Davis, D. W., J. Gray, G. L. Cumming, and H. Baardsgaard. 1977. Determination of the 87Rb decay constant. Geochimica et Cosmochimica Acta 41, no. 12:1745–1749.
Dickin, A. P. 2005. Radiogenic isotope geology, 2nd ed. Cambridge, United Kingdom: Cambridge University Press.
Egelkraut, K., and H. Leutz. 1962. β-spektrum und halbwertszeit des Rb87. Zeitschrift für Physik 161, no. 1:13–19.
Faure, G., and J. L. Powell. 1972. Strontium isotope geology. Berlin, Germany: Springer-Verlag.
Faure, G. and T. M. Mensing. 2005. Isotopes: Principles and applications, 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Flynn, K. F., and L. E. Glendenin. 1959. Half-life and beta spectrum of Rb87. Physical Review 116, no. 3:744–748.
Geese-Bähnisch, I. 1955. Zum β-zerfall des rubidiums 87: Nachpriifung des zerfallsschemas und neubestimmung der halbwertszeit. Zeitschrift für Physik 142:565–684.
Hahn, O., F. Strassman, and E. Walling. 1937. Herstellung wägbarer Mengen des Strontiumisotops 87 als Umwandlungsprodukt des Rubidiums aus einen kanadischen Glimmer. Naturwissenschaften 25, no. 12:189.
Hahn, O., and E. Walling. 1938. Über die Möglichkeit geologischer Alterbestimmungen rubidiumhaltiger Mineralien und Gesteine. Zeitschrift für anorganische und allgemeine Chemie 236, no. 1:78–82.
Hahn, O., F. Strassman, E. Walling, J. Mattauch, and H. Ewald. 1943. Geologische Alterbestimmungen mit der Strontiummethode. Chemie Zeitung 67:55–56.
Haxel, O., F. G. Houtermans, and M. Kemmerich. 1948. On the half-life of Rb87. Physical Review 74, no. 12:1886–1887.
Hiess, J., D. J. Condon, N. McLean, and S. R. Noble. 2012. 238U/235U systematics in terrestrial uranium-bearing minerals. Science 335, no. 6076:1610–1614.
International Union of Geological Sciences. 2014. International chronostratigraphic chart v.2014/02. Retrieved from the International Commission on Stratigraphy website at www.stratigraphy.org/index.php/ics-chart-timescale on June 19, 2014.
Kossert, K. 2003. Half-life measurements of 87Rb by liquid scintillation counting. Applied Radiation and Isotopes 59, no. 5–6:377–382.
Kovách, A. 1964 A re-determination of the half-life of rubidium-87. Acta Physics, Hungarian Academy of Sciences 17, no. 3:341–342.
Leutz, H., H. Wenninger, and K. Ziegler. 1962. Die halbwertszeit des Rb87. Zeitschrift für Physik 169:409-416.
Lewis, G. M. 1952. The natural radioactivity of rubidium. Philosophical Magazine 43, no. 345:1070–1074.
Mattauch, J. 1937. Das Paar Rb87-Sr87 und die Isobaren-regel. Naturwissenschaften 25:189–191.
MacGregor, M. H., and M. L. Wiedenbeck. 1954. The third forbidden beta spectrum of rubidium-87. Physical Review 94, no. 1:138–140.
McMullen, C. C., K. Fritze, and R. H. Tomlinson. 1966. The half-life of rubidium-87. Canadian Journal of Physics 44, no. 12:3033–3038.
McNair, A., and H. W. Wilson. 1961. The half-life of rubidium-87. Philosophical Magazine 6, no. 64:563–572.
Minster, J.-F., J.-L. Birck, and C. J. Allègre. 1982. Absolute age of formation of chondrites studied by the 87Rb-87Sr method. Nature 300:414–419.
Nebel, O., E. E. Scherer, and K. Mezger. 2011. Evaluation of the 87Rb decay constant by age comparison against the U-Pb system. Earth and Planetary Science Letters 301, no. 1–2:1–8.
Neumann, W., and E. Huster. 1974. The half-life of 87Rb measured as difference between the isotopes 87Rb and 85Rb. Zeitschrift für Physik 270:121–127.
Neumann, W., and E. Huster. 1976. Discussion of the 87Rb half-life determined by absolute counting. Earth and Planetary Science Letters 33, no. 2:277–288.
Nier, A. O. 1940. A mass spectrometer for routine isotope abundance measurements. Review of Scientific Instruments 11:212–216.
Papanastassiou, D. A., and G. J. Wasserburg. 1969. Initial strontium isotopic abundances and the resolution of small time differences in the formation of planetary objects. Earth and Planetary Science Letters 5:361–376.
Pinson, W. H., C. C. Schnetzler, E. Beiser, H. W. Fairbairn, and P. M. Hurley. 1963. Rb-Sr age of stony meteorites. MIT Geochronology Laboratory 11th Annual Report NYO-10:517.
Rotenberg, E., D. W. Davis, Y. Amelin, S. Ghosh, and B. A. Bergquist. 2012. Determination of the decay-constant of 87Rb by laboratory accumulation of 87Sr. Geochimica et Cosmochimica Acta 85:41–57.
Schmitz, M. D. 2012a. Radiogenic isotope geochronology. In The geologic time scale 2012, ed. F. M. Gradstein, J. G. Ogg, M. D. Schmitz, and G. M. Ogg, vol. 1, chapter 6, pp. 115–126. Amsterdam, The Netherlands: Elsevier.
Schmitz, M.D. 2012b. Radiometric ages used in GTS2012. In The geologic time scale 2012, eds. F. M. Gradstein, J. G. Ogg, M. D. Schmitz, and G. M. Ogg, vol. 2, appendix 2, pp. 1045–1082. Amsterdam, The Netherlands: Elsevier.
Shih, C.-Y., L. E. Nyquist, D. D. Bogard, J. L. Wooden, B. M. Bansal, and H. Wiesmann. 1985. Chronology and petrogenesis of a 1.8 g lunar granitic clast: 14321, 1062. Geochimica et Cosmochimica Acta 49:411–426.
Snelling, A. A. 2005. Isochron discordances and the role of mixing and inheritance of radioisotopes in the mantle and crust. In Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, pp. 393–524. El Cajon, California: Institute for Creation Research; Chino Valley, Arizona: Creation Research Society.
Snelling, A. A. 2014a. Radioisotope dating of meteorites: I. The Allende CV3 carbonaceous chondrite. Answers Research Journal 7:103–145.
Snelling, A. A. 2014b. Radioisotope dating of meteorites: II. The ordinary and enstatite chondrites. Answers Research Journal 7:239–296.
Steiger, R. H., and E. Jäger. 1977. Subcommission on geochronology: Convention on the use of decay constants in geo- and cosmochronology. Earth and Planetary Science Letters 36, no. 3:359–362.
Tetley, N.W., I.S. Williams, I. McDougall, and W. Compston. 1976. A comparison of K-Ar and Rb-Sr ages in rapidly cooled igneous rocks. Unpublished preprint.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2000. Radioisotopes and the age of the earth: A young-earth creationist research initiative. El Cajon, California: Institute for Creation Research; St. Joseph, Missouri: Creation Research Society.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2005. Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative. El Cajon, California: Institute for Creation Research; Chino Valley, Arizona: Creation Research Society.
Williams, I. S., N. W. Tetley, W. Compston, and I. McDougall. 1982. A comparison of K-Ar and Rb-Sr ages of rapidly cooled re-evaluated igneous rocks: two points in the Palaeozoic time scale. Journal of the Geological Society of London 139:557–568.
Zhao, W. R., and F. Käppeler. 1990. The 176Lu chronometer in trouble. In Astrophysical ages and dating methods (Proceedings of the Fifth IAP Workshop, June 26–30, 1989, Institut d’Astrophysique de Paris, France), ed. E. Vangioni-Flam, M. Cassé, J. Audouze, and J. Tran Thanh Van, pp. 357–364. Paris, France: Editions Frontières.









